从马尔科夫过程到吉布斯采样（附程序示例）

目标：如何采取满足某个概率分布的一组数据，比如如何给出满足标准正太分布的1000个点，当然该分布比较简单，生成满足此分布的1000个点并不难，对matlab，python 等都是一行语句的事，但是如果是一个不常见的分布，怎样采集呢？

本文试图通过示例让读者理解从马尔科夫链到Gibbs采样的各种采样方法的不断改进过程。

• Part 1       马尔科夫过程

马尔科夫假设： 当前状态发生的概率只跟直接相连的前面状态有关。

马尔科夫链示例如下：

---

某地区天气状态的转移概率矩阵P

	热	舒适	冷
热	0.7	0.25	0.05
舒适	0.65	0.2	0.15
冷	0.05	0.85	0.1

---

   假设将某地区天气状况分为热，冷，舒适，三种状态。转移概率矩阵P如上表所示。假设第一天的天气为热，问第100天的天气是怎样的？

根据所学的概率知识可知：

第二天：S2=[ 0.7   0.25   0.05 ]  即第二天70%可能继续热， 25%可能舒适， 很小可能冷。为表示

第三天: S3=S2*P=[0.655  0.2675 0.0775]

第四天：S4=S3*P=[0.63625  0.283125 0.080625]

。。。。。。。。。。。。。。。。。。。。。。。此处省略很多天

第98天： S98=S97*P=[0.632      0.28533333    0.08266667]

第99天： S99=S98*P=[0.632      0.28533333    0.08266667]

第100天： S100=S99*P=[0.632      0.28533333    0.08266667]

先不着急下结论，看如下问题：

问题2：  假设第一天天气为冷，问第100天的天气情况

解决方法同上，S2=[0.05 0.85 0.1]， S100=S2*P^99，经计算得

S100=[0.632      0.28533333    0.08266667]

问题3： 假设第一天天气为舒适，问第100天的天气情况

解决方法同上，S2=[0.65 0.2 0.15]， S100=S2*P^99，经计算得

S100=[0.632      0.28533333    0.08266667]。

现在从另一个角度审视状态转移矩阵P

P=[[0.7 , 0.25, 0.05],     
      [0.65, 0.2 , 0.15],
      [0.05, 0.85, 0.1 ] ]

P^2=[[0.655 , 0.2675, 0.0775],
        [0.5925, 0.33  , 0.0775],
        [0.5925, 0.2675, 0.14  ]]

P^3=[[0.63625 , 0.283125, 0.080625],
        [0.633125, 0.28    , 0.086875],
        [0.595625, 0.320625, 0.08375 ]]

。。。。。。。。。。。。。。。。。。。。。省略

P^10=[[0.63200006 0.2853333  0.08266664]
          [0.63200002 0.28533325 0.08266673]
          [0.63199944 0.28533387 0.08266668]]

。。。。。。。。。。。。。。。。。。。。。。

P^20=[[0.632      0.28533333 0.08266667]
          [0.632      0.28533333 0.08266667]
          [0.632      0.28533333 0.08266667]]

到此我们发现了一个神奇的现象 ,P若干次幂之后，在乘以P 矩阵也不会发生变化了。

定义：

• 最后那个不变的状态S 称为平稳分布（Stationary Distribution）有时也被称为均衡分布（Equilibrium Distribution）
• 细致平稳条件， S*P=S

综上可以得出如下结论：

• 不管初始状态如何，给定P后，万法归宗，最后的状态是一样的。
• 存在某一正数M 当N>M后， P^N=P^(>N)
• S 跟P的关系是 1 vs 多 P  P^2   P^3 ,最后都能归于平稳状态S。
• 如上条结论，满足细致平稳条件的P 有很多个。

马尔科夫采样： 前提，已知  P 

采样方法：

1 从某个初始分布S0（往往跟稳态分布不一样）出发，采样初始状态x0,

2 根据状态x_t和转移概率矩阵P(已知的)计算条件分布 S（）

3 从分布S采样

4 设置某个阈值，截取后半部分的采样序列。

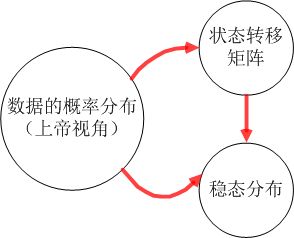
图1为遵循马尔科夫链的真实数据之间的关系，总体上三者是等价的。但是数据的概率分布是最真实的，也是唯一的，状态转移矩阵并不是唯一的，稳态分布是唯一的。

---

                                                           

                                                                               图1 马尔科夫链中的数据关系

---

•  Part 2       MCMC采样 与 M-H采样

从上一部分我们知道，如果给定一个待采样的分布,也就是平稳分布S，在知道与S 对应的P时，使用马尔科夫采样即可。但是在实际中，我们一般知道问题给出的分布，但是不知道分布对应的转移矩阵。

首先定义细致平稳条件（detailed balance condition） 设平稳分布为S,某转移矩阵为Q

如果S ,Q满足   则称矩阵Q满足平稳细致条件。上例中的P^10,P^20都满足次条件。

但是如果随意给定一个矩阵，则很难满足。

可以通过改造的方式让给定的Q满足条件，改造方式为,红色字体为改造的内容。

定义, 可以看出有点类似于后验概率的公式, 我们称之为接受率。

MCMC采样过程如下：

MCMC算法

输入：稳态分布S，转移矩阵Q,初始化状态链 方法： 假设t时刻状态为, 根据, Q采样备选值 a 从均匀分布采样 u~uniform[0 1] 如果u<=S(a)*Q(|a) 则接受转移 =a 否则=

MCMC采样有个问题，接受率往往很小，导致状态很少转移， 针对这一问题，出现了M-H采样，Metropolis-Hastings

M-H采样过程同MCMC一致，只是转移率取为 min[S(a)/S(x_t),1],可以看出如果a的稳态概率大于当前值的稳态概率，则一定转移，反之，则以一定的概率转移。

总结，MCMC 和M-H 可以理解为经过两次采样，第一次采样的值以一定的概率被接收。

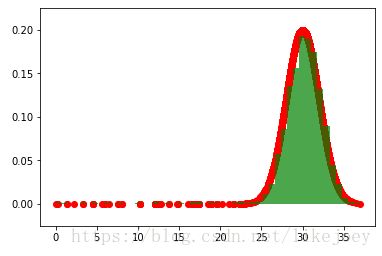
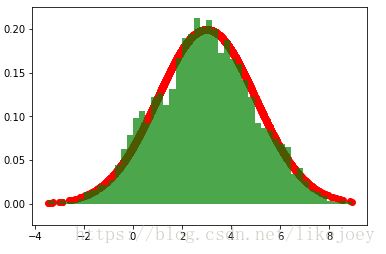
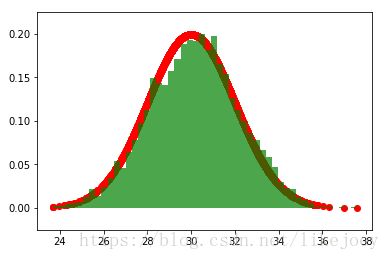
示例;图2 为M-H采样，目标数据的稳态分布为分别为均值是3/30方差为2的正太分布。转移概率为以转移点为均值，方差为1的正太分布。

从图中可以看出，如果初始值离稳态分布的均值差距很大，需要经过较长时间的采样后才能得到符合平稳分布的数据。

---

                

       图1（a）: 均值30， 50000个采样点中前5000个                            图1（c）: 均值3， 50000个采样点中前5000个 

                

    图1（b）: 均值30， 50000个采样点d的后5000个                              图1（d）: 均值3， 50000个采样点中后5000个 

                                                         图2 M-H采样

---

M-H采样的Python 代码。

import random
import math
from scipy.stats import norm
import matplotlib.pyplot as plt
#% matplotlib inline
pmu=3

def norm_dist_prob(theta):
    y = norm.pdf(theta, loc=pmu, scale=2)
    return y

T = 50000
pi = [0 for i in range(T)]
sigma = 1
t = 0
while t < T-1:
    t = t + 1
    pi_star = norm.rvs(loc=pi[t - 1], scale=sigma, size=1, random_state=None)
    alpha = min(1, (norm_dist_prob(pi_star[0]) / norm_dist_prob(pi[t - 1])))

    u = random.uniform(0, 1)
    if u < alpha:
        pi[t] = pi_star[0]
    else:
        pi[t] = pi[t - 1]

#plti=pi[T-5000:T-1]
plti=pi[0:4999]
plt.scatter(plti, norm.pdf(plti, loc=pmu, scale=2),color='red')
num_bins = 50
plt.hist(plti, num_bins, normed=1, facecolor='green', alpha=0.7)
plt.show()

 Part 3       Gibbs 采样

M-H采样推广到多维数据的情况。

为啥要Gibbs？ 数据的联合概率分布很难确定，尤其是高纬情况下。但边缘概率分布容易得到的情况。

Gibbs 采样过程：

• 输入平稳分布S(x1,x2)，设定状态转移次数阈值n1，需要的样本个数n2
• 随机初始化初始状态值x1_0和x2_0
• for t=0:n1+n2_1

          从条件概率分布P(x2|x1(t)中采样得到样本x2(t+1)

          从条件概率分布P(x1|x2(t+1)中采样得到样本x1(t+1)

Gibbs采样过程有点像坐标交替优化法。

示例：摘自注1

                                     

---

               

---

 

# -*- coding: utf-8 -*-
"""
Created on Sat Sep 15 11:19:05 2018

@author: Administrator
"""

from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt
import random
samplesource = multivariate_normal(mean=[5,-1], cov=[[1,0.5],[0.5,2]])

def p_ygivenx(x, m1, m2, s1, s2):
    return (random.normalvariate(m2 + rho * s2 / s1 * (x - m1), math.sqrt(1 - rho ** 2) * s2))

def p_xgiveny(y, m1, m2, s1, s2):
    return (random.normalvariate(m1 + rho * s1 / s2 * (y - m2), math.sqrt(1 - rho ** 2) * s1))

N = 5000
K = 20
x_res = []
y_res = []
z_res = []
m1 = 5
m2 = -1
s1 = 1
s2 = 2

rho = 0.5
y = m2

for i in xrange(N):
    for j in xrange(K):
        x = p_xgiveny(y, m1, m2, s1, s2)
        y = p_ygivenx(x, m1, m2, s1, s2)
        z = samplesource.pdf([x,y])
        x_res.append(x)
        y_res.append(y)
        z_res.append(z)

num_bins = 50
plt.hist(x_res, num_bins, normed=1, facecolor='green', alpha=0.5)
plt.hist(y_res, num_bins, normed=1, facecolor='red', alpha=0.5)
plt.title('Histogram')
plt.show()

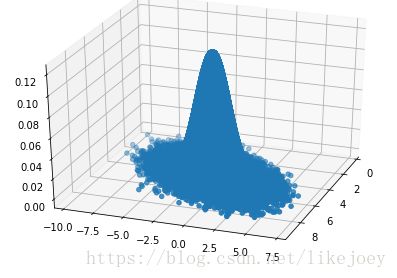
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(x_res, y_res, z_res,marker='o')
plt.show()

 

注1：（本文相关代码及部分理解来自https://www.cnblogs.com/pinard/p/6638955.html）作者讲的深入浅出，很详细。