Codeforces Round #628 (Div. 2) F. Ehab's Last Theorem（详解）

F. Ehab's Last Theorem

It's the year 5555. You have a graph, and you want to find a long cycle and a huge independent set, just because you can. But for now, let's just stick with finding either.

Given a connected graph with nn vertices, you can choose to either:

• find an independent set that has exactly ⌈n−−√⌉⌈n⌉ vertices.
• find a simple cycle of length at least ⌈n−−√⌉⌈n⌉.

An independent set is a set of vertices such that no two of them are connected by an edge. A simple cycle is a cycle that doesn't contain any vertex twice. I have a proof you can always solve one of these problems, but it's too long to fit this margin.

Input

The first line contains two integers nn and mm (5≤n≤1055≤n≤105, n−1≤m≤2⋅105n−1≤m≤2⋅105) — the number of vertices and edges in the graph.

Each of the next mm lines contains two space-separated integers uu and vv (1≤u,v≤n1≤u,v≤n) that mean there's an edge between vertices uuand vv. It's guaranteed that the graph is connected and doesn't contain any self-loops or multiple edges.

Output

If you choose to solve the first problem, then on the first line print "1", followed by a line containing ⌈n−−√⌉⌈n⌉ distinct integers not exceeding nn, the vertices in the desired independent set.

If you, however, choose to solve the second problem, then on the first line print "2", followed by a line containing one integer, cc, representing the length of the found cycle, followed by a line containing cc distinct integers integers not exceeding nn, the vertices in the desired cycle, in the order they appear in the cycle.

Examples

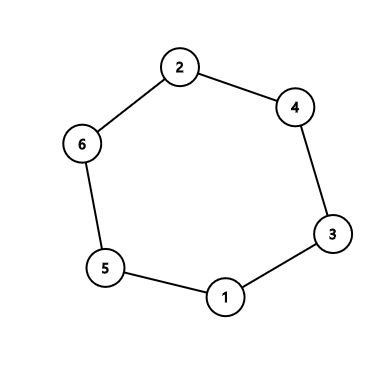
input

Copy

6 6
1 3
3 4
4 2
2 6
5 6
5 1

output

Copy

1
1 6 4

input

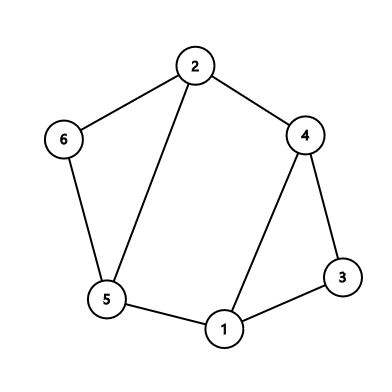
Copy

6 8
1 3
3 4
4 2
2 6
5 6
5 1
1 4
2 5

output

Copy

2
4
1 5 2 4

input

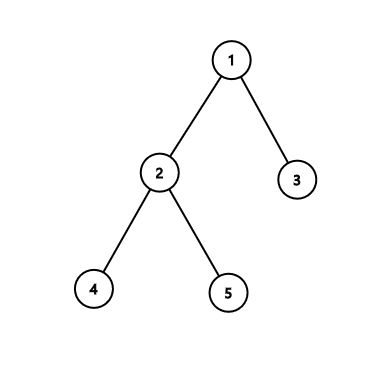
Copy

5 4
1 2
1 3
2 4
2 5

output

Copy

1
3 4 5 

Note

In the first sample:

转存失败重新上传取消正在上传…重新上传取消转存失败重新上传取消

Notice that you can solve either problem, so printing the cycle 2−4−3−1−5−62−4−3−1−5−6 is also acceptable.

In the second sample:

转存失败重新上传取消正在上传…重新上传取消转存失败重新上传取消

Notice that if there are multiple answers you can print any, so printing the cycle 2−5−62−5−6, for example, is acceptable.

In the third sample:

转存失败重新上传取消正在上传…重新上传取消转存失败重新上传取消

 题解：

/**
* pre【】满足sqrt（n）的路径，num【】记录涂0-(sqrt(n)-1)种颜色的点的数量，dep【】记录DFS时的深度，而涂什么颜色也是根据dep%（sqrt(N)-1)来涂的
* 关于为什么取sqrt(N)-1种颜色，如果取2种颜色，而sqrt（n）=4，存在某个环A-B-C-A，按2种颜色存的话就是0-1-0，而这时A和C颜色一样
* 那么此时输出的独立集可能会WA掉，因为A和C并不相互独立，而如果取大于sqrt(n)种颜色，而给的图是一条链，A-B-C-D，涂色的话就是0-1-2-3或者0-1-2-0
* 那么，此时也可能会WA掉，因为你不能保证你每次选择输出的颜色个数都正好存在某种颜色X刚好有sqrt（n）个，所以为了避免这样结果就取sqrt（N）种颜色
* 如果是一条直线，那么也一定存在sqrt（n）个点涂某一种颜色
* DFS的时候，任意选择一个点x，假设x是根节点，其余节点都是x的后代，按深度遍历的时候，
* 如果遍历的是环（假如环是A-B-C-D-E-A)，A的深度为5，那么其余分别对应的数字为B-6,C-7,D-8,E-9，遍历到A的时候，形成环，那么
* 就判断这个环的长度是否等于sqrt（n），如果是，就进行输出，输出的时候，pre【】记录的就是路径形成sqrt（n）环的路径，所以只需要反向遍历就可以将环输出
* 如果不等于sqrt（n）的话，A-5,B-6,C-7,D-8,E-9，的深度不变，涂的颜色也不会变，某种颜色的数量也不会改变
* 关于可能存在相邻两个点涂的颜色相同，那么考虑，DFS某一直链时，是否存在两个相邻的数%mod相等呢？很明显，不存在，除非n=1，而n>=5，所以不可能存在
* 那么最后一定存在颜色x,即num【x】>=sqrt（n），而x是由深度%（sqrt（n）-1）得出的，所以，枚举n个点的深度，如果%（sqrt（n）-1）==x，那么输出
*/

/// #include 
#include 
#include 
#include 
#include 
#include 
#include