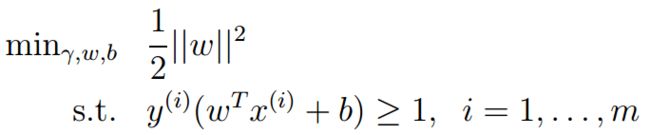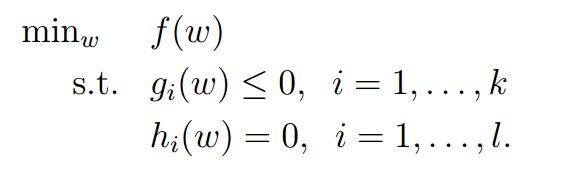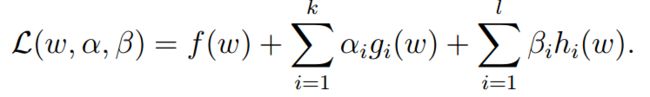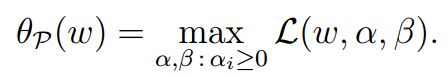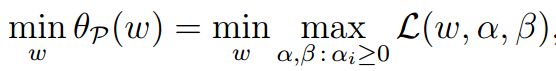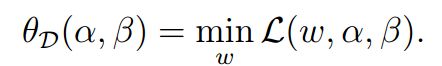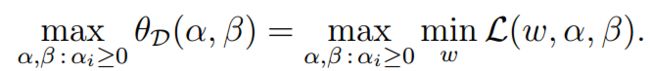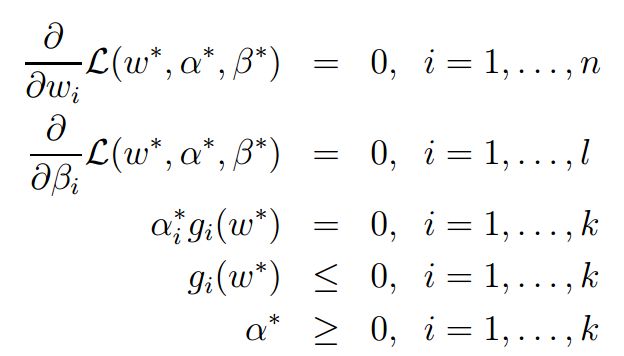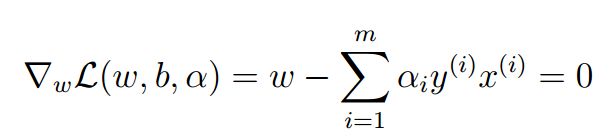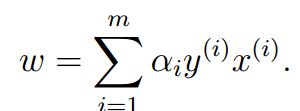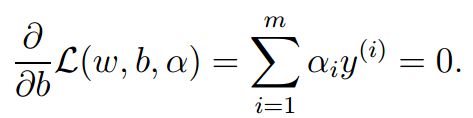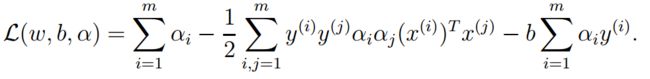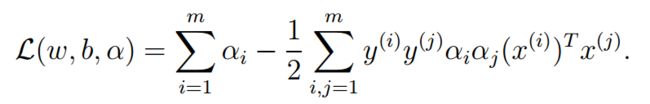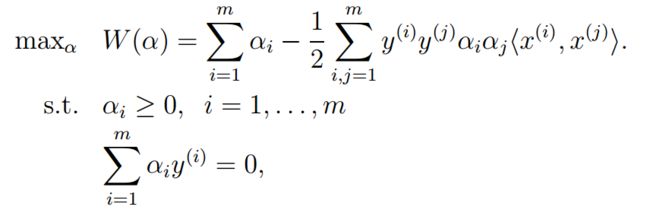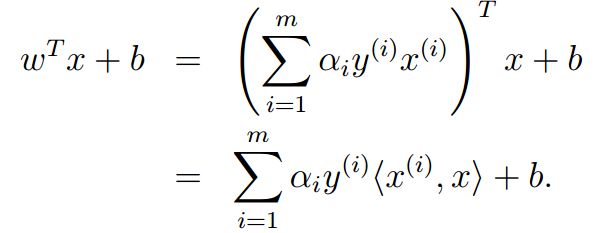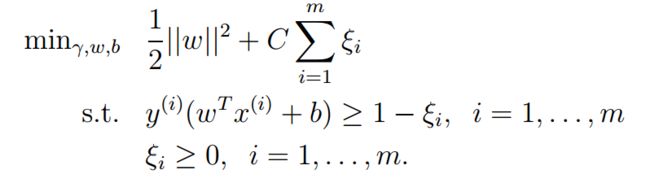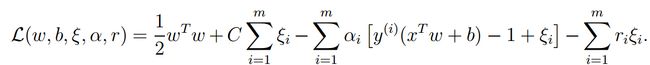机器学习（三） --- SVM学习：模型求解
学习SVM理论基础后，更进一步了解SVM算法就是了解SVM的算法的求解了，SVM算法的求解是一个凸优化问题，可以使用QP优化包进行求解，但是Platt提出了SMO算法，能够大大提升SVM模型的求解速度，这一节中主要就学习和掌握SVM算法的求解，会涉及到很多的数学公式，也是看了好久，查阅了好多资料，才从蒙蔽状态慢慢解放出来，然后对照着着比较简单的SMO算法，对照着算法流程，才慢慢变成半蒙蔽状态。
首先接着上一节理论基础遗留下的SVM算法的优化模型：
对于这种存在条件约束的优化问题，可以使用拉格朗日乘法来解决，学过高数的人，看着拉格朗日倍感亲切咯。
因此模型可以变成以下模型：
============================拉格朗日对偶性的讨论==============================
为了一般性的讨论问题，除了不等式条件，在这里，还引入等式条件，将上式一般化一下模型：
因此以拉格朗日处理以上模型的求解问题，得到：
将上述模型抽象为：
其中：
代表primal，即原始模型的求解。
所以得到以下等价模型：
接着提出一个对偶性问题：上边是最大值的最小化，对偶问题应该就是最小值的最大化，即：
可以很好的理解是：最大值的最小化大于等于最小值的最大化，对用一个式子的全局极值而言。因此可以得到以下关系：
在某种条件下，上式的等号可以满足，这个条件称为KKT条件：
其中：
是原始模型问题的的解，
则是对偶问题的解。
===================================题外话============================================
那么这里就有需要思考和注意的问题了，就是为什么要把问题转换到对偶问题的求解上来呢：
在原始模型问题的求解上，即最大化值得最小化问题上，最大化是通过对alpha和beta的优化求解，最小化是通过w优化求解。
而对偶问题的求解上，即最小化值得最大化问题上，最小化是通过w的优化求解，最大化则是通过alpha和beta的求解上。
因此经过处理后，我们可以把模型的求解转换到alpha的求解上，这个就能引入所谓的SMO算。
====================将拉格朗日对称性应用于SVM模型求解===========================
回到SVM的模型求解问题上：经过拉格朗日处理后，得到了以下模型:
求导：首先是实现最大化，对w求偏导：
得到关系式一：
对b求导，得到关系式二：
将关系式一带入到模型中，则得到：
由于关系二的原因，式子简化为：
因此最后的模型求解转化为：
其中需要注意的是，测试集的数据x的label的最后表达式为：
对于该式，有以下几点说明：
- 由于支持向量具有稀疏性，因此对于大部分
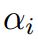的值为0，因此内积的计算仅仅只是测试数据与支持向量的内积，预算量较少 - 测试数据和支持向量均为列向量，因此避免了复杂的矩阵计算
- 这种内积性质可以很好的应用到核的概念中
经过一系列的推导，最终转换到了由的优化问题，从而求解模型优化。最后的式子是向量的内积的概念在其中，而我们上面讨论的问题都是以线性分类为基础的，从超平面的表达式就可以看出，对于非线性的分类问题呢？需要怎么求解，这就需要引出核的概念了。
核总的来说，就是一个映射函数，将一组特征向量，映射到高维的空间中，使得在低维空间不能线性分类解决的非线性问题，在高维空间内可以以线性概念解决。
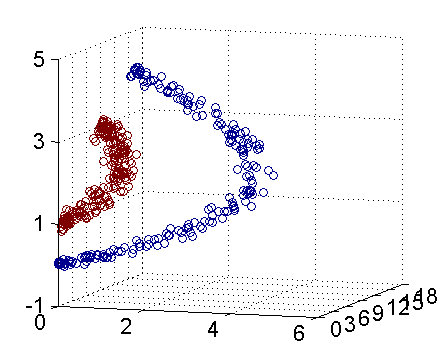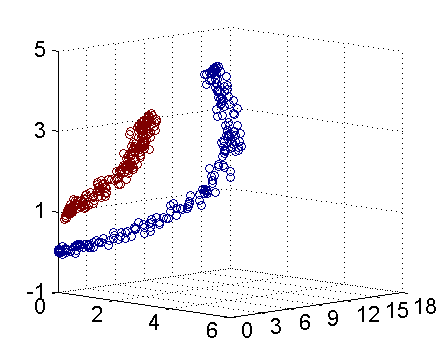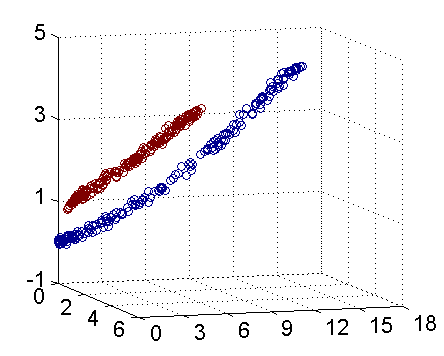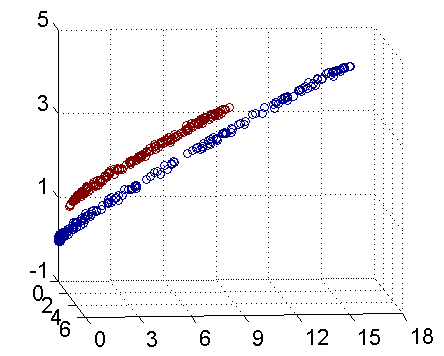
下面是一组关于利用核进行映射后的概念性的解释图：
二维空间 三维空间
可以明显看到，在三维空间内，可以找到一个平面实现非线性的分类。
对于核的具体描述和分析，可以参见以下博客：
- http://blog.csdn.net/abcjennifer/article/details/7849812
- http://blog.csdn.net/v_july_v/article/details/7624837
- http://cs229.stanford.edu/notes/cs229-notes3.pdf#page=1
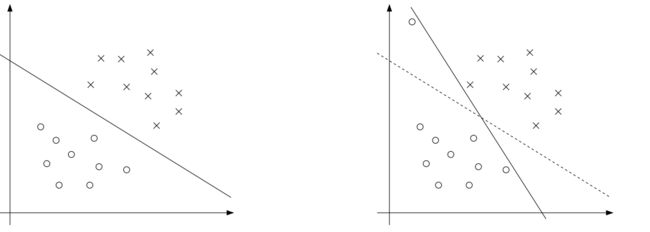
但是由于在映射过程中，并不能保证完全的线性化，如下图：
左图是一个最优的margin classfier的情形，但是由于部分数据点映射的问题，导致跑偏的情况，所以最后的分类是右图的情形，这个分类器就不是最优的情形。对于着心中数据点成为outlier。因此需要进行一定的正则化，控制这种情况。
其中C是为了控制margin最大的超平面和保证数据点的偏差最小的权重，是人为设定的。经过推导，仿照之前的拉格朗日的方法，得到：
从而得到：
对于这个问题，可以用过SMO算法有效的解决。以上是SVM的模型问题，下一节将会继续学习如何将SMO算法应用于该问题的求解中。