卡尔曼滤波通俗易懂的解释

关于卡尔曼滤波，网上的资料很多，但是有很大一部分都是不断堆叠公式，然后用各种晦涩难懂的专业术语进行解释，说实话我刚开始看的时候也是云里雾里，因此写下这篇博客是为了照顾和我一样的萌新，通篇文章我会力求从最基础的部分一步一步深入，并尽可能少地使用公式（或许？），对每个公式和参数也尽可能详尽地解释，所以通篇文章可能较长；另一方面，这篇博文也是为了自己日后方便回顾用的。如有错误请及时指出。

参考的部分资料如下：
如何通俗并尽可能详细地解释卡尔曼滤波？
如何理解那个把嫦娥送上天的卡尔曼滤波算法Kalman filter?
卡尔曼滤波器的原理以及在matlab中的实现
Understanding Kalman Filters
How a Kalman filter works, in pictures

文章中使用了部分资料的部分图片（侵删），废话不多说，直接开始我们学习卡尔曼滤波器之旅。

什么是卡尔曼滤波？

卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰影响，所以最优估计也可以看做是滤波过程（出自百度百科）。

从上面的解释我们可以提取出一些关键信息，首先，卡尔曼滤波是面向线性系统的（当然还有面向非线性系统的扩展卡尔曼滤波，这也是后话了）；其次，是一种估计系统状态的最优化算法。卡尔曼滤波一般用于机器人的状态估计较多，如移动机器人的位姿估算等。

如何通俗易懂地理解卡尔曼滤波？

这里我们就不扯那些专业术语了，我们讲“人话”。首先我们需要对卡尔曼滤波具体是干什么的要建立起一个最基本的概念，这里先借鉴知乎用户Kent Zeng的说法，给大家打一个大致的基础。

假设你现在处于某颗星球上，手上有两个力传感器，并且有一个已知质量为m的物体，但是你不清楚他们的重力大小，而且你也不知道你现在所处位置的重力加速度的具体值为多少，因此你打算通过两个传感器获得物体的重力。

但不幸的是它们测得的读数似乎每次都不太一样，那该怎么办？没错，就是取平均。

再假设你知道其中贵的那个传感器应该准一些，便宜的那个应该差一些。那有比取平均更好的办法吗？没错，加权平均。

再然后，假如你手上只有一个传感器，但是你碰巧得知了当地的重力加速度为g，那么你现在可以知道传感器测出的重力值为G1，你自己通过数学模型推导出来的重力G2 = mg，但是这两个值之间似乎也有偏差，那该怎么办呢？

没错，我们还是取两值的加权平均，但是你不清楚G1和G2哪个更加可信，那么如何确定权值系数？这取决于你对这个g值的确信度，如果你更相信数学模型mg的推导结果，那么对应数学模型的权值更大，而你传感器的观测模型的权值则变小；如果你对g的确信度较小，那么就正好相反。而这个权值，在卡尔曼滤波中也叫作卡尔曼系数。

以上，就是卡尔曼滤波最基本的思想。没错，是不是很简单呢？当然，在这之中我们也忽略掉了一些东西，但是不要着急，我们一步一步来。

卡尔曼滤波实际上就是把传感器测得的值和根据数学模型推导出来的值融合以逼近实际值的过程，因此卡尔曼滤波也经常被称作传感器融合算法。

更近一步的实例

现在，让我们更进一步地理解卡尔曼滤波的思想（下图均来自MATLAB官方卡尔曼滤波视频）。如果你对正态分布不太了解或者已经忘得差不多了，请你查看以下博客内容来回顾一下正态分布、方差、标准差等知识点。
高斯分布
平均值(Mean)、方差(Variance)、标准差(Standard Deviation)

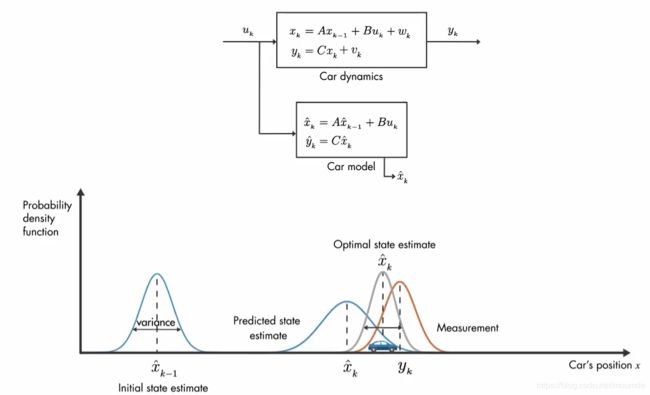
假设你现在有一辆车，并且已知小车在初始状态的位置如图所示服从正态分布（横坐标为小车前进坐标），有可能位于正态分布的均值附近。有人会问，为什么是正态分布而不是确定点呢？因为在这里我们给出的是它此刻的状态估计量，对于地图上的物体，我们无法确切得出其具体的位置信息，当你使用GPS来定位时始终会有一定的误差。因此你只能通过系统的输入（如小车的速度）和系统的输出（GPS给定的位置信息）来估算它当前的状态（真实的位置信息）。

当然，这里说多了，后续我们会详细展开讨论，这里你只要知道，小车在初始状态的位置估计是服从正态分布的。

然后，根据初始时刻小车的位置，我们可以预测出它在下一个时间步长的可能的位置分布。图中可以看出，它的正态分布函数明显比上一时刻来的更宽一些。这是因为在小车运动过程中会不可避免地遇到一些随机因素的干扰，如坑洼、风等，因此我们估算的位置值的不确定性变大，小车实际经过的距离与模型预测的距离不同。

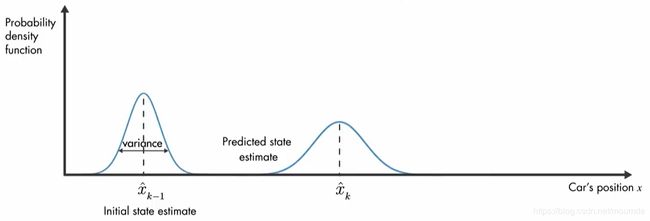
上述过程均是由我们的数学模型推算估计出来的结果，但是，我们也知道，相同的数据，我们也可以通过传感器测量来获取，而测量值往往也呈正态分布并且与我们的模型预测值有所不同，如下图中红色正态分布曲线所示，方差表示噪声测量中的不确定性。

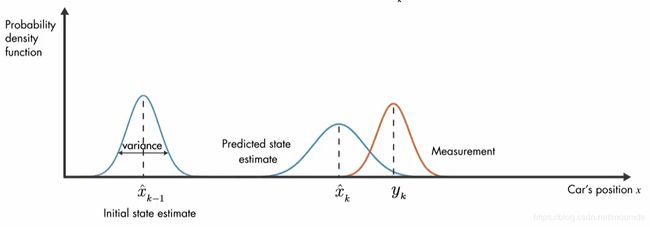
那么，通过上一个小节的学习，你知道了，我们可以通过将我们的模型预测值与传感器的测量值相互结合起来来获得小车的最佳位置估计值。具体的结合过程我们后续讨论，这里你可以简单当做我们把这两者的概率密度函数相乘得出了当前时刻的最佳状态估计值，如图中灰色正态分布曲线所示。

再然后，我们把前面的时间信息换一下，比如我们知道了上一时刻即k-1时刻小车的位置估算值，并且通过数学模型预测得到了k时刻的位置估算值，然后将其与小车传感器的测量值进行结合，得到了当前k时刻小车的最佳位置估算值。

那么问题来了，这里我们并没有给出初始状态，因此k-1时刻的位置估算值又是怎么来的呢？没错，我们是通过k-2时刻的状态量估算的来了。这就引出了我们卡尔曼滤波在连续时间段内的迭代操作。

以上，通过本小节的学习，你已经在原来的基础上更深一步地理解了卡尔曼滤波的思想：

1. 卡尔曼滤波是利用线性状态模型，以及模型的输入和输出值，结合传感器测量值获取当前时刻的最佳状态估计值；
2. 卡尔曼滤波假设所有的不确定性因素理论上都服从正态分布；
3. 卡尔曼滤波就是使最后估算状态的高斯分布的期望值能够接近实际值，并且方差够小；
4. 卡尔曼滤波工作于连续的系统，并通过迭代操作估算每一个时刻的最佳状态估计值。

结合线性系统模型再来看看

通过之前的学习，相信你已经对卡尔曼滤波建立起了一个初步的印象，如果你是科普性质的学习，那么到上一小节为止已经足够了。但是，如果要更深一步，我们还必须结合各种公式来深入探讨一下。当然，我会尽可能用通俗易懂的语言来进行描述。

在开始学习之前，请你先简单回顾一下方差、协方差以及协方差矩阵的一些基本概念。
方差、协方差、相关系数的理解
概率笔记8——方差、均方差和协方差
如果有同学还没有学习过现代控制理论，建议先去学一下，至少先知道状态空间模型是什么。

在我们之前的讨论过程中，我都是尽可能避免公式的堆叠，用图文的方式进行解释。现在，让我们重新回看一下上一小节的小车模型。不过，在此之前，我们先定义三个变量，在这里，你只要先简单记住这些变量的含义就行了。

$x$ —— 状态量的真实值
$\hat{x}$ —— 状态量的估计值
${\hat{x}}^{-}$ —— 根据上一步估计值推算出来的当前时刻预测值（并不是最终的估计值）

有人会对 $\hat{x}$ 和 ${\hat{x}}^{-}$ 的差别有疑问，我这里先简单解释一下，$\hat{x}$ 表示的是最终的估计值，${\hat{x}}^{-}$ 表示的是不完整的估计，也就是还需要进行修正。简单点说就是 ${\hat{x}}^{-}$ 是 $\hat{x}$ 的未完成版。

还是原来那个小车模型，这次我们结合小车的线性模型来进行讨论。首先假定下图所示是我们真实的小车模型（这个模型指的是真实的小车系统，并不是我们用来推算的数学模型，也就是说对于我们来说，我们并不清楚方框内部的方程），它仅有一个状态量，即用$x_k$来表示某一时刻车的真实位置，我们往往不能直接得到$x_k$的值。系统的输入为速度$u_k$，而车的位置$y_k$ 我们通常由GPS进行定位得到。

$x_k=A{x}_{k-1}+B{u}_k$ 表示系统的状态预测方程，A表示状态转移矩阵，表示如何从上一时刻状态推算当前时刻状态；B为控制矩阵，表示控制量 $u$ 如何作用于当前状态（这里由于只有一个状态量，因此A和B都是标量）。

$y_k=C{x}_k$ 表示系统的观测方程，当前模型在理论情况下$y_k$应该和$x_k$是相等的，也就是$C=1$。

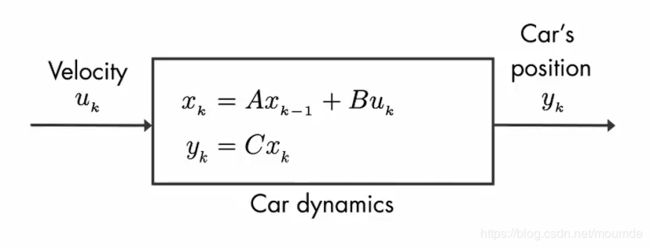
但是在真实的环境下，GPS的测量往往是不准确的，并且会伴随着测量噪声，因此我们需要在观测方程后面加上噪声干扰，用$v$进行表示。

而同样的，我们的小车在实际运行过程中也会不可避免地受到一些随机因素的影响，因此我们在状态方程后面同样加上过程噪声，用 $w$ 表示，那么实际的小车模型可以表示为：

我们相信随机噪声 $w$ 和 $v$ 是服从正态分布的。

现在，假定你的数学基础非常的好，你给出了小车系统的数学模型。通过下方的小车数学模型（Car model），你可以将输入量（速度$u_k$）输入到你给出的数学模型中推算出小车位置的估计值 $\hat{x}$（注意这里的C = 1，也就是说 $\hat{y}$ = $\hat{x}$ ）。

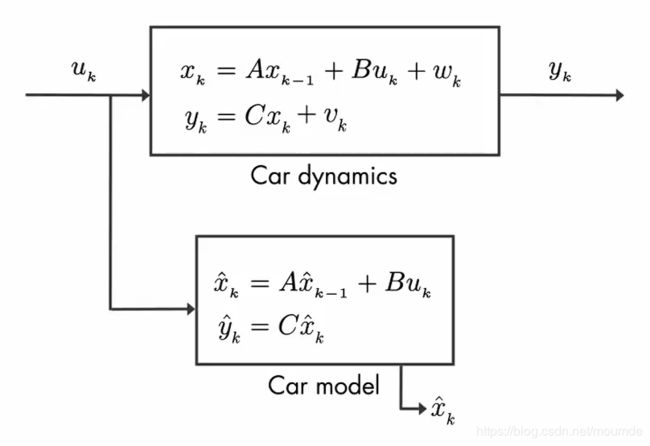
那么，卡尔曼滤波器的作用，就是把GPS测量得出的传感器测量值 $y_k$ 和你用数学模型推导出的估计值 $\hat{x}$（其实是 $\hat{y}$，只不过这里两者相等）相结合，得出对小车的最佳位置估计。

图中，我们再次强调，Car dynamics是小车的真实模型，内部的方程我们是不清楚的，这里只是为了更好地示意真实噪声环境下传感器测量结果的不确定性，我们能得知并且运用的，只有输入量 $u_k$ 和传感器测量值 $y_k$；而 Car model 则是我们实际运用的数学模型，我们可以从中得出状态估计量 $\hat{x}$。

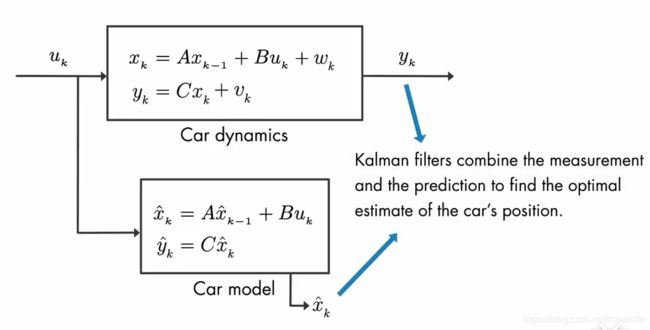
那么，现在我们再把示意图加进去，再仔细理解一下，发现是不是瞬间通顺了很多？

卡尔曼滤波器的实际推导

讲了这么多，所以卡尔曼滤波到底是怎么实现的呢？接下来我们将通过小车模型进行实际的推导。

还是原来的模型，我们现在想获得最接近实际值的估计值 $\hat{x}$。一种比较简单的方式就是将数学模型的估计值 $\hat{y}$ 逼近实际值 $y_k$，即令 $error=y-\hat{y}$ 趋于0，这样最后得到的 $\hat{x}$ 也将会接近于实际值 $x_k$。这听上去像不像反馈控制呢？我们可以借鉴类似的思想。

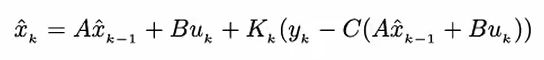
这里直接给出了卡尔曼滤波器的公式，是不是感觉很熟悉呢？公式中括起来的第一部分就是我们原先的Car model中的 $\hat{x}$的计算公式，只不过在后面我们加上了相应的修正。

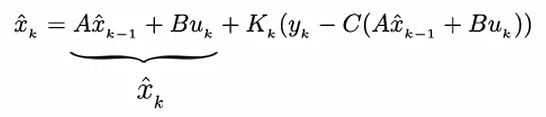
因此，我们可以得知之前给出的 ${\hat{x}}_k=A{\hat{x}}_{k-1}+B{u}_k$ 它是不完整的，后续还需要进一步的修正，因此在这里用 ${\hat{x}}_k^{-}$ 来表示，称为先验概率。

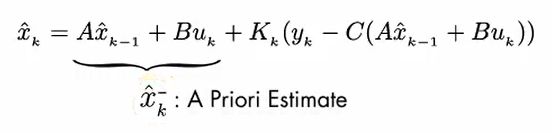
因此，可以进一步简化为如图所示公式。原模型的观测方程表示为：${\hat{y}}_k=C{\hat{x}}_k$。由此可知，后面的 $y_k-C{\hat{x}}_k^{-}$表示的就是测量值减去估计值，将其合并到预测中以更新估计值，$K_k$即为卡尔曼系数，表示更新的权重，后面这部分也被称为后验估计。

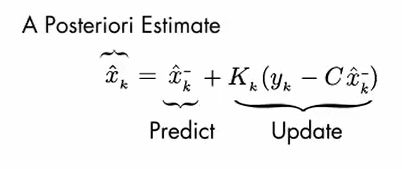
那么，最后我们可以得到卡尔曼滤波的完整公式，如图所示。它主要分为两部分，包括预测部分和更新部分。看上去是不是有点麻烦？没关系，我们一步一步来看。你只需要记住，其他5个方式实际上就是为了我们上面图中推导出来的那个状态估计公式所服务的。

预测模型

首先是预测部分，其内部主要分为两个公式：
状态预测公式：${\hat{x}}_k^{-}=A{\hat{x}}_{k-1}+B{u}_k$
协方差预测公式：$P_k^{-}=A{P}_{k-1}{A}^T+Q$

其中 $A$ 表示状态转移矩阵，$B$ 表示控制矩阵，$P$ 表示噪声协方差矩阵，$Q$ 表示预测模型自带的噪声。

我们必须知道，在推测时都是包含噪声的，噪声越大，系统的不确定性也就越大，而每一个状态的不确定性通常由协方差矩阵 $P$ 来表示，那么如何让这种不确定性在每个时刻进行传递呢？这边直接给出答案，就是通过 $A{P}_{k-1}{A}^T$在两侧分别呈上状态转换矩阵以及它的转置，但是我们的模型也并非百分之百准确，因此需要在之后加上噪声 $Q$。

关于协方差的意义具体查看：
方差、协方差、相关系数的理解
概率笔记8——方差、均方差和协方差

通过上面两个公式即可用上一时刻的状态来预测当前时刻的状态，得到带 “-” 号的 ${\hat{x}}_k^{-}$和 $P_k^{-}$。“-” 号表示该值该欠缺一部分，需要从观测值处获得补充的信息。

状态更新模型

状态更新这部分主要包含3个公式：
卡尔曼系数：$K_k=\frac{P_k^{-}{C}^T}{C{P}_k^{-}{C}^T+R}$
状态估计： ${\hat{x}}_k={\hat{x}}_k^{-}+K_k(y_k-C{\hat{x}}_k^{-})$
噪声协方差矩阵更新：$P_k=(I-K_{k}C)P_k^{-}$

其中 C 表示观测矩阵，R表示观测量协方差矩阵。

最重要的就是其中的状态估计公式，其余五个公式进行运算实际上都是为了这个状态估计公式来服务的。它将原本的预测值进行更新，即加上一个残差（实际观测值与预期观测值之间的差），这个残差还需要乘上一个卡尔曼系数，将预测值和乘上卡尔曼系数的残差进行相加，即可得到我们最后的最佳状态估计值。

卡尔曼系数 $K_k$ 的推导较为复杂，我们不详细展开，这里主要说明一下它的作用：

1. 权衡预测状态协方差矩阵P和观测量协方差矩阵R的大小来觉得对预测模型和观测模型的确信度。如果相信预测模型多一些，那么 $K_k$ 会相应小一些，如果相信观测模型多一些，那么 $K_k$ 会相应大一些；
2. 把残差的表现形式从观测域转换到状态域。因为在实际运用过程中都是采用矩阵形式，而 $y_k$ 和 ${\hat{x}}_k$ 两个向量之间的元素个数很可能不同，因此通过这种运算完成转换。

最后通过噪声协方差矩阵更新公式来利用卡尔曼系数更新最佳估计值的噪声分布。此次得到的协方差矩阵是留给下一次迭代时使用的。