旅行商问题(华为笔试蜜蜂采蜜问题)
旅行商问题是算法中比较难的一类题目,也是比较综合的题目之一,其变种的题目也非常灵活,应用场景非常广泛,前段时间在做华为笔试题目的时候,遇到了一个与旅行商问题相关的蜜蜂飞行采花粉问题:
题目大意是:一个蜜蜂从蜂窝出发,在五朵花上采蜜之后,要飞回蜂窝,题目给出蜂巢和5朵花在二维空间中的坐标,求蜜蜂走完全程的最短路程。
这是典型的旅行商问题的应用,但是当时因为对旅行商问题不是很熟悉,为了快速写完代码,直接用了全排列(DFS)去做,但是复杂度是指数级的,6个节点还好,一旦节点变多必会出现超时情况。
旅行商问题描述:该类问题的最优解要求的是除了起始节点外,其他每个节点只能经过一次,也就是说,所有节点的入度和出度都只能是1,(旅行商问题有个特点,通常是所有节点之间都可以自由连同,因为只有每个节点至少有两个度,才能画出一个不回头的路线),画出沿途路径之后就是哈密顿图,如下所示:
解决旅行商问题有很多种:
1、上述提到的permutation方法属于直接暴力法,这种方法在节点情况比较少的时候可以通过,但是,基本没啥技术含量,不容易出错,因此可以用它来做对数器。
2、DFS深度优先遍历也是解决该问题中比较好的方法,属于贪心算法,从一个点开始不断的遍历下去,最终找到一个最短的方案,在该题目中,复杂度是指数级的,但是可以有效处理某些点之间不通的问题,避免无效运算。
3、动态规划是我们常用到的方式,一般动态规划是从暴力方法中提取出来的,但是,该题目中动态规划的思路不是很好想,也正因为该方法不好想,所以针对动态规划来进行分析。但是所有的动态规划,其本质都是来源于暴力求解,在直观点说,dp和dfs密不可分,二者都是采用了分治策略,只是dp会对状态量进行保存,避免了重复计算,如何对DFS改写DP,请大家参考左神的课程,我觉得讲的很好。
首先,假设共有4各点,0为起始点,从0点出发,经过1、2、3点之后回到0点为一个完整过程,这个过程实际上是0 -> (1、2、3)->0,表示的是从0点出发经过1、2、3这个集合的所有点之后回到0点,实际上我们可以把过程分解为:(0->k)和((S)->0)两个过程,其中,k是(1、2、3)集合中的一个点,S是不包含k的集合,举个例子:假定k选择的是1号点,我们需要求出0->1之间的距离 d11,在求出1->(2、3)->0的最短距离 d12,总路程d1 = d11+d12。同理,假设k选择的是2号点,我们相应求出距离d2,假设k选择的是3号点,我们相应求出距离d3,然后选择d1,d2,d3中的最小值,min(d1, d2, d3),得到最终结论,至于子过程1->(2、3)->0,也可以通过 上述方法求得结果,顺着该思路,可以直接写出DFS代码,但是,DFS代码因其不保存状态,使得有些状态量会反复参与运算,造成复杂度升高,而此方案中,dp方案依然是指数级。
有了以上的推论,我们知道,一个点(i)通过某一个集合(j)到达初始点(0)的过程可以表示为两个子过程的加和,选择点k,则 d[i][j] = c[i][k]+d[k][l],c[i][k]表示点i到点k的距离,l表示j集合中除了k点其他点组成的集合。也就是说,当知道了集合 j 中每一个元素通过其剩下元素组成的集合后返回起始点的距离,用一个for循环在比较,求出所有方案中的最小值,即为最优解。
为了方便理解,可以将上述过程用一张dp表来表示:
|
|
{} |
{1} |
{2} |
{1、2} |
{3} |
{1、3} |
{2、3} |
{1、2、3} |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 0 |
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
j集合中表示的点为该数二进制中为为1的位置,哪个位上为1,标志哪个点在该集合内,例如,集合3的二进制为011,表示(1,2),集合7的二进制为111, 表示(1,2,3)。
dp[0][0]表示从起始点经过空集返回,长度为0。 d[0][1]表示从起始点出发,经过集合1返回起始点,过程是:0->1->0,结果是2倍的0->1的距离.
d[1][2]表示从点1出发,经过集合2返回起始点,过程是:1->2->0,结果是1->2和2->0这两段的距离和。 dp[2][1]表示从点2出发,经过集合1返回起始点,过程是:2->1->0,结果是2->1和1->0这两段的距离和,而dp[0][2]可以表示:
dp[0][2] = max(c[0][1]+dp[1][2], c[0][2]+dp[2][1])同理,不断计算每个对应位置的数值,求得最终的结果:
dp[0][7] = max(c[0][1]+dp[1][6], c[0][2]+dp[2][5], c[0][3]+dp[3][3])通过一个具体的例子来进行说明,
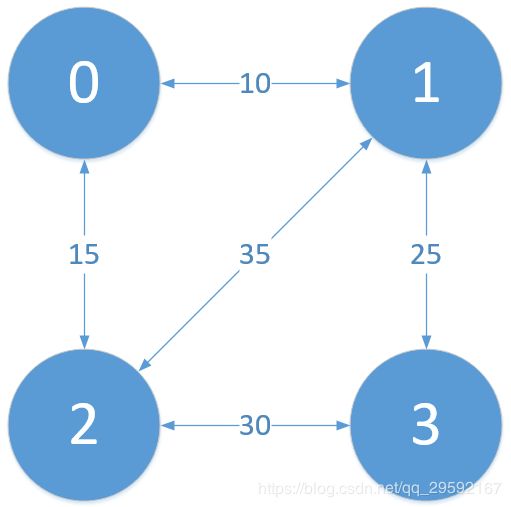
根据上述算法,对该拓扑结构中的距离进行求解,然后开始填dp表,根据递推关系应该按列填,第一列是点i到起始点的距离,因此,
for (int i=0; i其中,上述代码的graph变量为邻接矩阵。
此后安列填空,因为每一列都要用到前几列的信息,所以,该编码形式下无法进行空间压缩。
后续代码:
for (int j=1; j0 && j&(1<<(i-1))) {
continue;
}
for (int k=1; k 上述代码的意思是,因为需要按列填空,所以,表示dp列信息的j作为第一层循环,表示行信息的i为第二层循环,首先判断i是否在j中,i不能在j集合中,这是前提,因此,需要加入判断语句。在j集合中选择一个点,但是,这里我们无法直接判断出j中包含的点数,所以,只能遍历所有点,加入判断,k点是否在j中,只有当k在j中时,才进行操作。
另外,我的代码中,所有的dp初始值和不通的情况都是用-1表示的,因此,要加入额外判断,避免出现求解问题,即,如果某些值为-1,表示该路不通,则不去参与数值更新。填空结果如下:
|
|
{} |
{1} |
{2} |
{1、2} |
{3} |
{1、3} |
{2、3} |
{1、2、3} |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 0 |
0 |
20 |
30 |
60 |
-1 |
-1 |
-1 |
80 |
| 1 |
10 |
-1 |
50 |
-1 |
-1 |
-1 |
70 |
-1 |
| 2 |
15 |
45 |
-1 |
-1 |
-1 |
65 |
-1 |
-1 |
| 3 |
-1 |
35 |
45 |
75 |
-1 |
-1 |
-1 |
-1 |
以下是整个代码的实现如下:
#include
using namespace std;
class Solution {
public:
int shortestPath (vector>& graph, int N) {
int col = 1<<(N-1);
vector> dp (N, vector (col, -1));
for (int i=0; i0 && j&(1<<(i-1))) {
continue;
}
for (int k=1; k> N >> P;
vector> routes = {{0, 1, 10}, {0, 2, 15}, {1, 2, 35}, {1, 3, 25}, {2, 3, 30}};
vector> graph (N, vector (N, -1));
for (int i=0; i> x >> y >> z;
graph[x][y] = z;
graph[y][x] = z;
}
Solution solve;
solve.shortestPath(graph, N);
return 0;
}
因为即使是动态规划下,旅行商问题的复杂度依然是指数级的,因此,该问题一般不会出现很大的数据集,而现实生活中,要解决该类问题,可以使用蚁群,启发式等算法来解决,通过加入孙子节点,来判断等等,这里就不展开来讲了,有兴趣的同学可以百度,都有代码,但整体复杂度都不低。