动画 | 什么是基数排序?
基数排序和计数排序一样无需进行比较和交换,和桶排序一样利用分布和收集两种基本操作进行排序。基数排序是把每一个元素拆成多个关键字,一个关键字可以在每一个元素上同等的位置进行计数排序,一个元素拆成多个关键字可以看作是要进行几轮分桶,以一个元素最长的长度为准。
基数排序可以看成多(单)关键字的排序,可以想象成桶排序那样分桶排序,也可以像计数排序那样归约化分治。
基数排序的思想是将待排序序列中的每组关键字进行桶排序。例如整数序列[103, 9, 1,7,11,15, 25, 201, 209, 107, 5]上每个位、十位和百位上的数字看成是一个关键字。
基数排序有两种方式进行,一种是LSD,从右边关键字开始排序,另一种是MSD,从左边关键字开始排序。
基数排序LSD
我们将输入数组[103, 9, 1,7,11,15, 25, 201, 209, 107, 5],从右边关键字开始,以个位数上开始分桶,对于数字,每一个关键字取值范围是0~9,最多需要10个桶。如果是字符,按ASCII码最多需要128个桶,看情况而定。
为了保证元素之间的稳定性,就按计数排序一样,将给出一个统计数组c,长度为10,统计输入数组每一个元素对应的关键字。然后从统计数组c第2个位置开始,进行当前一项和前一项的累加。累加完之后反向填充数组b,也将数组b直接复制到数组array。
再进行循环操作exp *= 10,以十位数上进行分桶,直到超过某个元素的最长长度。
动画:LSD
基数排序
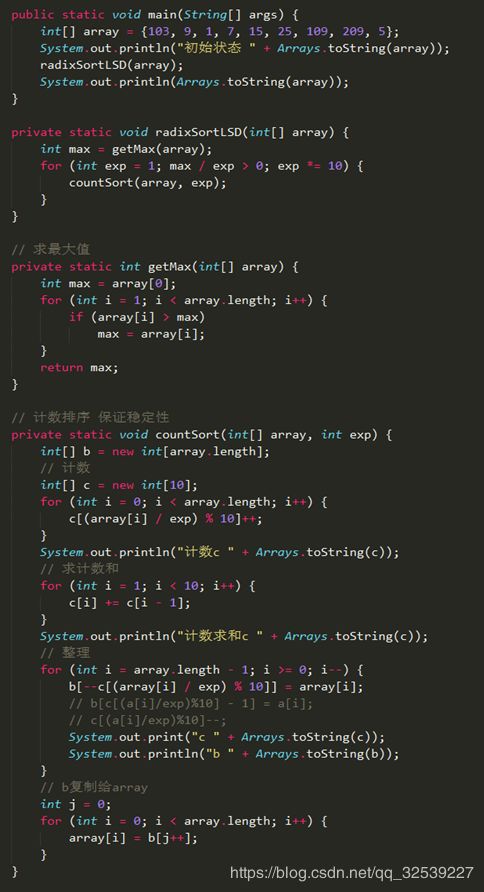
Code
Result
初始状态 [103, 9, 1, 7, 15, 25, 109, 209, 5]
计数c [0, 1, 0, 1, 0, 3, 0, 1, 0, 3]
计数求和c [0, 1, 1, 2, 2, 5, 5, 6, 6, 9]
c [0, 1, 1, 2, 2, 4, 5, 6, 6, 9]
…
b [1, 103, 15, 25, 5, 7, 9, 109, 209]
计数c [7, 1, 1, 0, 0, 0, 0, 0, 0, 0]
计数求和c [7, 8, 9, 9, 9, 9, 9, 9, 9, 9]
……
计数c [6, 2, 1, 0, 0, 0, 0, 0, 0, 0]
计数求和c [6, 8, 9, 9, 9, 9, 9, 9, 9, 9]
c [5, 8, 9, 9, 9, 9, 9, 9, 9, 9]
b [0, 0, 0, 0, 0, 25, 0, 0, 0]
……
b [1, 5, 7, 9, 15, 25, 103, 109, 209]
[1, 5, 7, 9, 15, 25, 103, 109, 209]
基数排序MSD
基于MSD方式的基数排序不能像LSD方式循环操作,它是将大问题分解成小问题进行基数排序的。
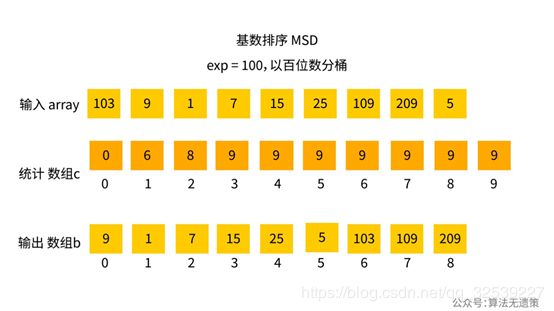
如果输入数组[103, 9, 1,7,11,15, 25, 201, 209, 107, 5],从左边关键字开始,以百位数上开始分桶,进行完一次计数排序之后可以看到上面输出的数组b[9, 1, 7, 15, 25, 5, 103, 109, 209],如果还是按照前面的步骤分桶和计数排序,这组数组就已被打乱了,103、109和209这三个数在十位上为0,是最小的,不符合基数排序。
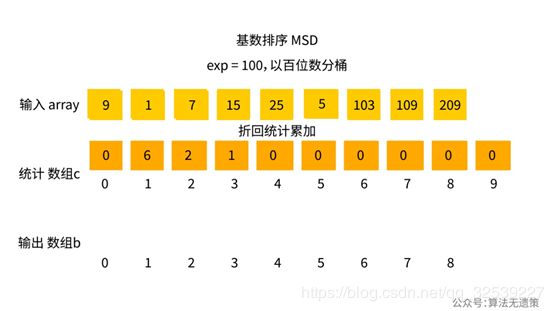
最好的方式是将大问题分解成一个个可以解决符合基数排序的小问题。上一次按百位数上开始分桶之后,还要将折回之前的数组c统计累加的过程。
设置数组array的low和high的位置,值可以获取折回统计累加之后的数组c上对应的值。数组array中[9, 1, 7, 15, 25, 5], [103, 109], [209]的长度和统计数组c上的[6, 2, 1]刚好对应,所以当进行递归方式的时候low和high上的值可以从数组c中获取,exp上的指数也对应的除以10,递归终止条件正是exp <= 0。
动画:MSD
基数排序
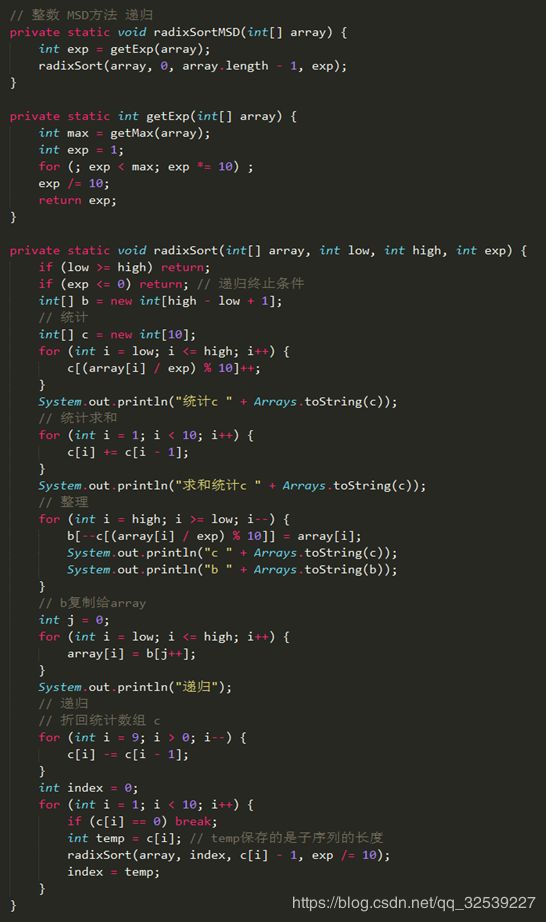
Code
Result
初始状态 [103, 9, 1, 7, 15, 25, 109, 209, 5]
统计c [6, 2, 1, 0, 0, 0, 0, 0, 0, 0]
求和统计c [6, 8, 9, 9, 9, 9, 9, 9, 9, 9]
c [5, 8, 9, 9, 9, 9, 9, 9, 9, 9]
b [0, 0, 0, 0, 0, 5, 0, 0, 0]
c [5, 8, 8, 9, 9, 9, 9, 9, 9, 9]
b [0, 0, 0, 0, 0, 5, 0, 0, 209]
c [5, 7, 8, 9, 9, 9, 9, 9, 9, 9]
b [0, 0, 0, 0, 0, 5, 0, 109, 209]
……
c [0, 7, 8, 9, 9, 9, 9, 9, 9, 9]
b [9, 1, 7, 15, 25, 5, 0, 109, 209]
c [0, 6, 8, 9, 9, 9, 9, 9, 9, 9]
b [9, 1, 7, 15, 25, 5, 103, 109, 209]
递归
统计c [4, 1, 1, 0, 0, 0, 0, 0, 0, 0]
求和统计c [4, 5, 6, 6, 6, 6, 6, 6, 6, 6]
c [3, 5, 6, 6, 6, 6, 6, 6, 6, 6]
b [0, 0, 0, 5, 0, 0]
c [3, 5, 5, 6, 6, 6, 6, 6, 6, 6]
b [0, 0, 0, 5, 0, 25]
c [3, 4, 5, 6, 6, 6, 6, 6, 6, 6]
b [0, 0, 0, 5, 15, 25]
c [2, 4, 5, 6, 6, 6, 6, 6, 6, 6]
b [0, 0, 7, 5, 15, 25]
c [1, 4, 5, 6, 6, 6, 6, 6, 6, 6]
b [0, 1, 7, 5, 15, 25]
c [0, 4, 5, 6, 6, 6, 6, 6, 6, 6]
b [9, 1, 7, 5, 15, 25]
递归
统计c [0, 1, 0, 0, 0, 1, 0, 1, 0, 1]
求和统计c [0, 1, 1, 1, 1, 2, 2, 3, 3, 4]
c [0, 1, 1, 1, 1, 1, 2, 3, 3, 4]
b [0, 5, 0, 0]
c [0, 1, 1, 1, 1, 1, 2, 2, 3, 4]
b [0, 5, 7, 0]
c [0, 0, 1, 1, 1, 1, 2, 2, 3, 4]
b [1, 5, 7, 0]
c [0, 0, 1, 1, 1, 1, 2, 2, 3, 3]
b [1, 5, 7, 9]
递归
[1, 5, 7, 9, 15, 25, 103, 109, 209]