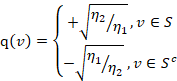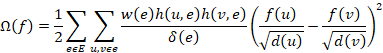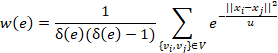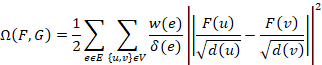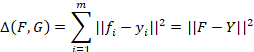超图学习（Hypergraph Learning）

1、基本概念

在数学上，图（Graph）是表示对象与对象之间关系的一种方式。图中的每个顶点表示一个对象，顶点之间的边用来描述对象之间的关系。普通图一般用一个二元组来表示，表示图的顶点集，表示图的边集，如图所示。

普通图

普通图一般用于描述存在二元关系的一组对象，即对象之间不存在多元关联关系。在计算机视觉和机器学习的问题中，我们一般假设对象之间的之间无关联关系或者为简单的二元关联关系，在该假设下，我们可以通过普通图解决很多问题。但是，在现实生活中对象之间的关系往往是更为复杂的单对多或者多对多的多元关联关系，如文献的引用关系就是一个典型的多对多关联关系，一篇论文可以引用多篇论文，且一篇论文也可以被多篇论文引用。在解决该类问题时，如果简单的把多元关系强制转换为二元关联关系，那么将会丢失很多有用的信息.

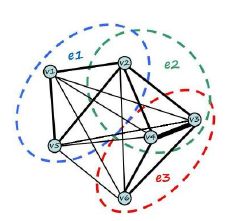
近些年来，一种普通图的推广变体——超图（Hypergraph）被提了出来，超图学习（Hypergraph Learning）也逐渐被引入用来解决计算机视觉和机器学习上的问题。相对于普通图而言，超图可以更加准确的描述存在多元关联的对象之间的关系。超图与普通图的主要不同在于图中边上顶点的个数的不同，在普通图中，，一条边包含两个顶点，在超图中，边被称为超边（hyperedge），一条超边包含多个顶点。如果一个超图中，所有的超边最多只包含两个顶点，那么超图就会退化为普通图，如下图所示。

超图

和普通图的二元组表示法类似，一个超图一个通过一个三元组来表示。给定一个超图,是超图的有限顶点集，是超图的超边集，是超边的权重集，对于任意一条超边是顶点集V的一个子集。在普通图中，顶点度（Degree）的定义为包含该到的边的个数，在超图中，顶点的度的定义如下：

对于超边而言，超边的度的定义为超边上包含的顶点的数目：

定义两个方阵、，分别表示超图的顶点的阶与超边的阶。类似于普通图的矩阵表示法，超图也可以通过构造一个维的点边关联矩阵H来表示。在关联矩阵中，如果一个顶点e在一条超边v上，则,否则。根据关联矩阵的定义，超图中点的阶和超边的阶可以进一步表示为：

2、超图分割

很多超图问题可以通过超图分割来解决。对于一个给定的超图而言，超图分割指的是存在一条超图切（Hypergraph Cut）把超图的顶点集分割为两个子集，一个是顶点集，另一个是其补集。对于子集S而言，我们可以将其超边边界定义为一个超边集：

该超边集将超图的顶点集分割为和两个子集。子集的体积定义为该顶点到中所有的顶点的阶之和：

则，顶点子集的超边边界的体积可定义为：

由上式可以看出，对于子集S与其补集Sc而言，两者的超图边界的体积是相等的，即。所以，我们可以把超边边界的体积看做两个顶点子集之间的连接紧密度，而顶点子集的体积可以看做是子集内部顶点之间的连接紧密程度。类似于普通图的图切问题（Graph Cut），对于超图分割，我们同样试图找到一个超图切。这个超图切将超图分割为两个子集，两个子集之间的连接程度是稀疏的，而子集内部顶点之间连接是紧密的。所以，我们可以将超图分割问题转化为下面的优化问题：

在上式中，表示超图的两个顶点子集之间的边界的体积，与分别表示两个顶点子集的体积。根据文献，可以得知超图切的最优化目标与一个瑞利商一致。假设一个列向量，其维度为超边中的顶点的个数，其元素值为：

在上式中，与分别表示与。由上式，可以将超图切的优化目标转化为：

矩阵是一个对角矩阵，对角线上的元素的值为。在上式中，涉及一个图学习中的重要概念——拉普拉斯矩阵。拉普拉斯矩阵是图的一种矩阵表示,是一个对角矩阵，，为图的度矩阵，为图的邻接矩阵。更长用到的是拉普拉斯矩阵的标准化表示，即。在超图中，超图的拉普拉斯矩阵可以表示为：

在上式中，表示超图的点边关联矩阵，若顶点在超边上，则，否则为0。前文假定的向量q被认为是超图的切向量。由此可以分析出，超图的最优化切割问题的解转化为了最小化向量q的问题，该问题是一个组合优化问题。从数学的角度分析该最优化问题，求解满足条件的最小化向量q就是求解矩阵束的最小特征值对应的特征向量。根据文献可知，上述问题的简化解可以从求解下式的最小非负特征值对应的特征向量来得到：

在上式中，I是一个单位矩阵，上式的结果就是超图的标准化拉普拉斯矩阵。对于超图分割问题而言，可以进一步的将优化目标函数推导成标准化损失函数，如下所示：

其中，向量就是超图切，如果从图嵌入的角度来思考该优化结果，向量也可以被看成是超图的嵌入。

3、超图正则化属性预测器（HAP）

3.1、属性超图

对于给定的一个数据集X而言，可以通过一个超图来描述数据集中样本之间的属性关系。属性（Attribute）即是用来描述每个样本所具有的特性的关键词，如颜色、有没有尾巴等。在超图中，每个样本对应超图中的顶点。对于超图的超边的构建，将具有同一个属性的样本归到同一条超边里。因为每个样本具有若干个属性，所以一个顶点可以属于多条超边，如果在该数据集中有个属性，那么超图就具有条超边。因为我们通过该超图来描述数据之间的属性关系，所以我们称该超图为属性超图。

假定一个维二值矩阵为该超图的点边关联矩阵，其中矩阵元素的值定义如下：

与前文中提到的超图的构建方式相同，我们定义超边的阶为超边包含的顶点的个数，由上式可以得到：

超图的顶点的阶定义为经过该顶点的所有超边的权重之和，如下：

前文中，我们并没有提及超边的权重的定义方式。在超图中，超边的权重的定义方式根据实际情况而选定，在本文中，我们假定超边的权重为超边上任意两个顶点之间的热核距离的平均：

同时，矩阵、、分别为、、的对角阵形式。

3.2、超图正则化属性分类器

超图学习在计算机视觉与机器学习上应用时，一般采用标准化超图来描述数据之间多元关联关系，即前文中所提到的。本节中所介绍的超图正则化属性预测器的主要思想来源于基于标准化超图的直推模型，但是与基于标准化超图的直推模型不同的是，超图正则化属性预测器是一个有监督的模型，在对属性预测器进行训练时，构建超图所用到的数据全部为有标签的数据。

前文提到，超图分割的目标是使得不同属性的样本之间的连接程度尽量稀疏，同属性样本之间的样本到的连接程度尽量紧密，换而言之，也就是超图切应该尽量不破坏样本之间的属性关系。同时一个样本具有多个属性，所以，在该算法中，超图正则化属性预测器的最终学习结果是一组切向量，而不是一个切向量。根据前文中所推导的超图分割的损失函数，可以将属性超图分割的损失函数定义如下：

在上式中，是描述训练集样本之间的属性关系的标准化超图拉普拉斯矩阵，是训练集样本在该超图切下的属性预测值。所以为了达到更佳的属性预测结果，在最小化超图切的同时，还应该进一步的最小化训练集样本的预测属性与真实属性之间的误差，该误差值采用欧氏距离进行描述，即：

在上式中，矩阵是训练集样本的属性标签矩阵。不难看出，属性标签矩阵可以通过属性超图的点边关联矩阵来构造出来，即。如果将该约束项添加到HAP算法的损失函数中，可以得到：

在上式中，是一个用于权衡超图切损失与分类损失的正参数。通过求解上式，可以得到一组既能满足最优化属性超图分割，又能使得属性的预测结果误差尽量小的切向量。

可以将超图的分割问题看作一个超图嵌入的问题，得到的超图切向量就是超图的一组嵌入向量。所以，属性超图的分割问题就可以被看成是一个特征空间到属性空间的嵌入过程。这样，超图正则化属性预测器的求解问题就可以被转化为求解一个样本特征空间的到属性空间对其的超图嵌入的映射问题。假定样本对应的映射矩阵为，则对应的映射过程如下:

与此同时，可以对损失函数添加一个二范式约束，用于避免在求解最优化超图切的过程中产生的过拟合问题。与正参数λ的作用类似，正参数η用于控制对二范式约束的惩罚。超图切的损失函数可以进一步被改写为：

拉普拉斯矩阵具有一些特殊的性质，由前文可知拉普拉斯矩阵是一个对称矩阵，同时拉普拉斯矩阵是半正定的。所以，上式损失函数的求解可以转化为一个正则化最小二乘法问题的求解，对投影矩阵求偏导即可求解，求解过程如下：

对于未知属性的图像样本z，可以通过投影矩阵B将其从视觉特征空间投影到属性空间获得其属性值：

源码：https://github.com/ZhouFengtao/MachineLearning/tree/master/HAP

论文：https://arxiv.org/abs/1503.05782