深入浅出多目标优化--10分钟多目标优化入门

多目标优化快速入门

多目标优化--引子

正如生活中，你想买一辆车，又想汽车的性能好，外观不错，价格还比较低，对于这同时满足这三个条件，我们应该如何进行考虑呢？

在投资的时候，我们想投入的资金最少，所付出的风险最小，同时收益是最大的，如何同时进行实现呢？

在数学学习中，求求函数 f1(x1,x2,…,xn)=x1^2+x2^2 +…+xn^2 及函数 f2(x1,x2,…,xn)=(x1-1)^2+(x2-1)^2 +…+(xn-1)^2 同时达到最小的 (x1,x2,…,xn) 的取值，不存在一组 (x1,x2,…,xn) 的取值，使 f1 和 f2 同时达到最小值，这时候怎么办呢？

帕累托最优

帕雷托最优是指资源分配的一种理想状态。帕雷托最优的状态就是不可能再有更多的帕雷托改善的状态；换句话说，不可能再改善某些人的境况，而不使任何其他人受损。

进化计算

最早的是达尔文的进化论-物竞天择，适者生存

后来是约翰.霍兰德提出的遗传算法

1.遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，通过模拟自然进化过程搜索最优解。

2.该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。

3.遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

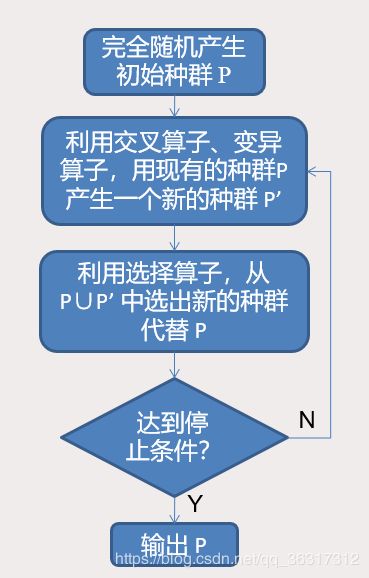
具体步骤是：

(1)种群中个体随机初始化.

(2)每个个体通过评价得到一个适应度值.

(3)适应度值大的个体有更大的概率保留下来.

(4)通过对适应度值大的个体交叉变异产生新的个体.

不断的迭代第 (2)-(4) 步骤，经过足够多的迭代次后，最终能得到好的解.

 

基本概念

MOP

1.求解单个函数 f1 的最小值为单目标优化问题(SOP)

2.同时求解多个函数 f1 和 f2 的最小值为多目标优化问题(MOP)

3.多目标优化问题的一般数学描述：

 

4.对于两个个体 X1 和 X2 以及目标函数 F(X)，若 X1 的每一个目标函数值 fi(X1) 都比 X2 对应的目标函数值 fi(X2) 要小，则认为 X1 要比 X2 更好，称 X1 支配(dominate) X2 ，记作 X1 ≺ X2 (它具有传递性)

5.若存在 i 和 j 使得 fi(X1) < fi(X2) 且 fj(X1) > fj(X2)， 则认为 X1 和 X2 无法比较，视为一样好，称 X1 与 X2 是非支配 (non-dominated)的，记作 X1 ⊀ X2 且 X2 ⊀ X1

6.对于一组个体，若 Xa 不被其它任何一个个体支配，则 Xa 也称为是非支配的；Xa 也叫做 Pareto 最优解

7.对于一个多目标优化问题，目的是求出一组 Pareto 最优解 Xi ，i=1,2,…，并使得目标函数的值尽可能地小

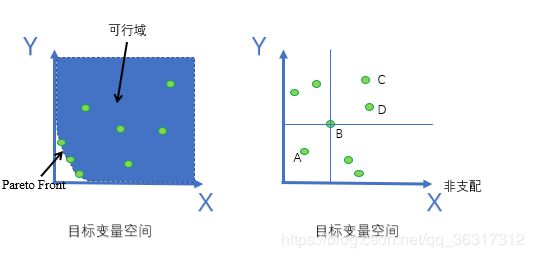
根据左图中目标变量可知 ，帕累托最优解往往在左下角，值相对偏小。

 

在右图中，可以看出，B支配C,D两点，在A点，B是被支配的，其余空间则是非支配

EC

1.想要求得多目标问题的最优解，我们利用计算机强大的计算能力，在决策空间中随机产生大量个体，并找出其中最好的(不被支配的)个体。也就是不断地“试”，来找到越来越好的个体。随机寻找个体的过程称为 搜索

2.但无法做到遍历决策空间中每一个个体，我们需要在更短的时间里利用随机的方法找到更好的个体

3.利用进化算法的策略，可以朝着越来越好的方向随机产生个体，而不是在决策空间中完全盲目地产生个体

4.作为一个随机性算法，进化算法有如下 特点：

•得到的不是问题的精确结果，而是近似的结果

•每次得到的结果不一样

•结果的精度随着迭代次数的增加而不断上升

•往往以算法得到的结果的精度来评价算法的性能

                    进化算法的一般策略

 

Indicator

 

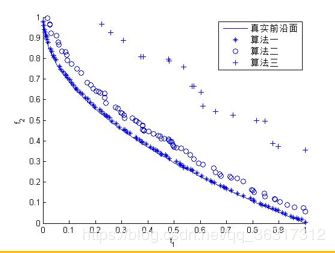
1.不同的算法，产生的结果是不同的，从结果可以看出各个算法性能的好坏

2.算法产生的解集的好坏标准：

•接近真实前沿面（收敛性）

•在空间上分布性好（分布性）

3.还有许多量化的评价解集的好坏的标准

发展历程

古典多目标时期

传统的多目标优化方法是将各个子目标聚合成一个带正系数的单目标函数，系数由决策者决定，或者由优化方法自适应调整。

为了获取近似Pareto最优集，一些优化方法使用不同的系数来实施动态优化。

常见的古典方法有加权法（利用斜率来判断最优解）、约束法、目标规划法以及极大极小法等

进化多目标时期

最早提到可以利用EA来解决多目标优化问题的是Richard S. Rosenburg 于1967年在他的博士论文 “Simulation of genetic populations with biochemical properties”中

David Goldberg 于1989年首次提出了Pareto Ranking的概念：MOEA中个体必须经由Pareto支配关系来选出，同时他也指出了MOEA中分布性保持的重要性，主要采取Fitness Share的策略

Carlos M. Fonseca 和 Peter J. Fleming 于1993年提出了Multiobjective Optimization Genetic Algorithm (MOGA)。MOGA采用基于排序数的适应度赋值机制以及自适应的适应度共享的策略，风靡一时

Kalyanmoy Deb于1994年提出了Non-dominated Sorting Genetic Algorithm (NSGA)，采用分层的非支配排序机制以及适应度共享机制。然而算法缺陷是计算复杂度为O(MN3)，随后，Deb跟他的学生在2000年提出了NSGA的改进版本NSGA2，文章于2002年发表TEVC。NSGA2采用快速非支配排序以及拥挤距离的策略，时间复杂度在O(MN2)。由于其速度及效果上的优势，许多年来NSGA2都被作为对比算法。

Eckart Zitzler 在1998年一个会议上提出Strength Pareto Evolutionary Algorithm (SPEA)，第二年文章被TEVC收录。SPEA在算法中使用了一个外部Archive来保留搜索到的好解，称之为Elitism。Elitism的使用随后也开始流行，随后不久Zitzler等人又对SPEA进行了改进SPEA2，主要引入了较细的适应度赋值方式以及密度估计方式（Truncation Method）。

2006年，张青富跟李辉首次提出了基于分解的多目标优化算法，MOEAD，是将MOP问题分解成SOP问题并同时对这些子问题进行优化。MOEAD不仅在速度上有优势，而且搜到的结果很规律。在MOEA领域开辟了一条新的通道。

2014年，Deb的NSGA3分成上下两个部分发表在TEVC上。主要是用来处理高维多目标问题。采用了基于参考点以及分解的策略。是NSGA2 + MOEAD 的结合

其中目前最经典的算法还是NSGA-II 和MOEAD,

请持续关注，后期会总结出这些算法的文章。