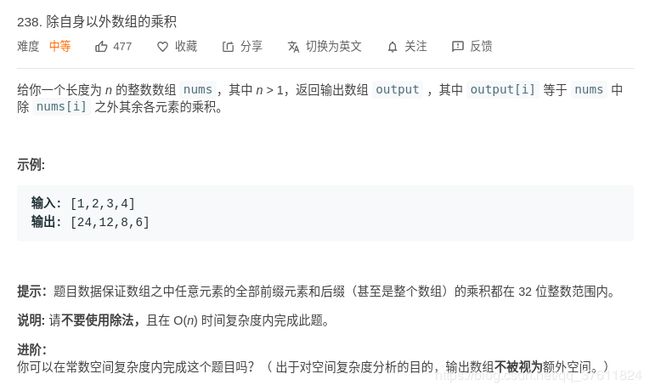
LeetCode 238 除自身以外数组的乘积

 

参考链接:https://leetcode-cn.com/problems/product-of-array-except-self/solution/chu-zi-shen-yi-wai-shu-zu-de-cheng-ji-by-leetcode-/

解题思路:利用索引左侧所有数字的乘积和右侧所有数字的乘积(前缀和后缀)相乘来解决.

我的解法:

class Solution {
public:
    vector productExceptSelf(vector& nums) {
        //解法一:
        int size=nums.size();
        vectorresult(size);

        for(int i=0;i

提交出现问题:超出时间限制

还存在一个编译错误问题:

Runtime Error
Line 924: Char 9: runtime error: reference binding to null pointer of type 'int' (stl_vector.h)
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior /usr/bin/../lib/gcc/x86_64-linux-gnu/8/../../../../include/c++/8/bits/stl_vector.h:933:9

原因是: vectorresult(size);错误初始化为vectorresult( );正确的形式就是vectorresult(size);

LeetCode官网上的解法:

方法一:是构建3个数组,L,R,answer

算法:

1. 初始化两个空数组 L 和 R。对于给定索引 i，L[i] 代表的是 i 左侧所有数字的乘积，R[i] 代表的是 i 右侧所有数字的乘积。
2. 我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L，L[0] 应该是 1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * nums[i-1]。
3. 同理，对于数组 R，R[length-1] 应为 1。length 指的是输入数组的大小。其他元素：R[i] = R[i+1] * nums[i+1]。
4. 当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i]

class Solution {
public:
    vector productExceptSelf(vector& nums) {
        int length = nums.size();

        // L 和 R 分别表示左右两侧的乘积列表
        vector L(length, 0), R(length, 0);

        vector answer(length);

        // L[i] 为索引 i 左侧所有元素的乘积
        // 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
        L[0] = 1;
        for (int i = 1; i < length; i++) {
            L[i] = nums[i - 1] * L[i - 1];
        }

        // R[i] 为索引 i 右侧所有元素的乘积
        // 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
        R[length - 1] = 1;
        for (int i = length - 2; i >= 0; i--) {
            R[i] = nums[i + 1] * R[i + 1];
        }

        // 对于索引 i，除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for (int i = 0; i < length; i++) {
            answer[i] = L[i] * R[i];
        }

        return answer;
    }
};

方法二：空间复杂度 O(1)的方法

思路

尽管上面的方法已经能够很好的解决这个问题，但是空间复杂度并不为常数。

由于输出数组不算在空间复杂度内，那么我们可以将 L 或 R 数组用输出数组来计算。先把输出数组当作 L 数组来计算，然后再动态构造 R 数组得到结果。让我们来看看基于这个思想的算法。

算法

1. 初始化 answer 数组，对于给定索引 i，answer[i] 代表的是 i 左侧所有数字的乘积。
2. 构造方式与之前相同，只是我们试图节省空间，先把 answer 作为方法一的 L 数组。
3. 这种方法的唯一变化就是我们没有构造 R 数组。而是用一个遍历来跟踪右边元素的乘积。并更新数组 answer[i]=answer[i]*Ranswer[i]=answer[i]∗R。然后 RR 更新为 R=R*nums[i]R=R∗nums[i]，其中变量 RR 表示的就是索引右侧数字的乘积。

class Solution {
public:
    vector productExceptSelf(vector& nums) {
        int length = nums.size();
        vector answer(length);

        // answer[i] 表示索引 i 左侧所有元素的乘积
        // 因为索引为 '0' 的元素左侧没有元素， 所以 answer[0] = 1
        answer[0] = 1;
        for (int i = 1; i < length; i++) {
            answer[i] = nums[i - 1] * answer[i - 1];
        }

        // R 为右侧所有元素的乘积
        // 刚开始右边没有元素，所以 R = 1
        int R = 1;
        for (int i = length - 1; i >= 0; i--) {
            // 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
            answer[i] = answer[i] * R;
            // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
            R *= nums[i];
        }
        return answer;
    }
};