一步步带你看懂orbslam2源码--单目初始化(五)

---

ORB-SLAM2目录：

   一步步带你看懂orbslam2源码–总体框架(一)
   一步步带你看懂orbslam2源码–orb特征点提取(二)
   一步步带你看懂orbslam2源码–单目初始化(三)
   一步步带你看懂orbslam2源码–单应矩阵/基础矩阵,求解R,t(四)
   一步步带你看懂orbslam2源码–单目初始化(五)

---

回顾:
  前面我们已经讲解了orbslam2中的理论环节,包括了RANSAC随机采样一致性算法,阈值的选择缘由,对极约束的原理,单应矩阵和基础矩阵的计算,如何从单应矩阵或基础矩阵中分解出R,t,单目初始化单应矩阵或基础矩阵选择策略等.本章节我们将主要进行单目初始化的理论环节,话不多说,接下来就直接进入正题.

---

理论环节

  先贴上Track()函数的整体框架代码,首先第一次执行时,mState将会默认等于NO_IMAGES_YET,也就是说系统将会进行一次初始化,然后初始化成功之后的每次运行,系统将不会再次进入if(mState==NOT_INITIALIZED)处的内容 (除非跟踪丢失,重定位?还没看完,暂时不清楚) ,即每次将会进入else{…}部分进行前端跟踪.

  由于本系列教程,我们是针对单目SLAM进行讲解的,所以接下来我们将进入MonocularInitialization();进行单目初始化.

  同样的,我们先来看来看一下该函数的主要框架.首先,系统将会选择一张图像特征点数量大于100的图像作为参考帧,并将该帧中的特征点作为预匹配特征点存入mvbPrevMatched向量中.什么意思呢?什么叫做预匹配点呢?其实由于单目初始化时,系统假设在两帧之间的位移很少(即对于参考帧中的特征点对应帧2中的匹配点,该匹配点与帧1特征点位置很接近),所以在寻找帧2匹配点时,将以帧1中特征点的位置的周边一小块区域作为搜索对象.不知道同学们听懂了没有…emm…假设大家都已经听懂了…下面给出总体框架的流程图

  也就是说,系统将会选择当前帧作为参考帧(如果该帧特征点数量>100),然后与下帧进行匹配,如果匹配失败,则将更新参考帧,并再与下帧进行匹配,以此类推,直至匹配成功.
接下来我们将讲解如下函数:

// Find correspondences
ORBmatcher matcher(0.9,true);
//输入参数:mInitialFrame,mCurrentFrame这是待匹配的两帧图片
//mvbPrevMatched为预匹配点坐标,函数运算后将会更新为真正的匹配点坐标
//mvIniMatches为mInitialFrame帧中的特征点在mCurrentFrame帧中的匹配点的索引
//100为搜索的区域边长,源码中是正方形的边长
//return 成功匹配的数量
int nmatches=matcher.SearchForInitialization(mInitialFrame,mCurrentFrame,mvbPrevMatched,mvIniMatches,100);

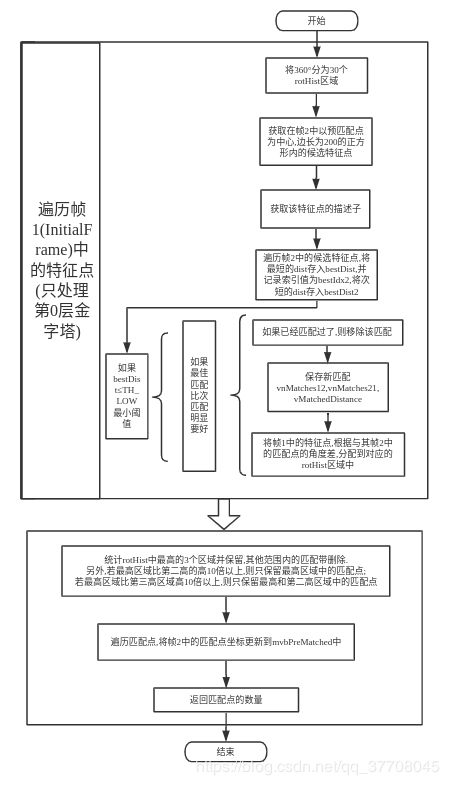
让我们来看看SearchForInitialization()函数的总体流程图吧

  该函数篇幅相对较长,但是基本上都不会怎么难,这里只是给出了整体的操作流程,相信读者们可以自行阅读懂该函数.好了,当匹配成功之后,系统将会执行以下程序计算相机的POSE,并且创建初始地图.

        //匹配成功,计算POSE
        cv::Mat Rcw; // Current Camera Rotation
        cv::Mat tcw; // Current Camera Translation
        vector<bool> vbTriangulated; // Triangulated Correspondences (mvIniMatches)

        if(mpInitializer->Initialize(mCurrentFrame, mvIniMatches, Rcw, tcw, mvIniP3D, vbTriangulated))
        {
            //剔除三角测量失败的匹配点
            for(size_t i=0, iend=mvIniMatches.size(); i<iend;i++)
            {
                if(mvIniMatches[i]>=0 && !vbTriangulated[i])
                {
                    mvIniMatches[i]=-1;
                    nmatches--;
                }
            }

            // Set Frame Poses
            //初始帧pose设置为单位矩阵
            //更新当前帧pose
            mInitialFrame.SetPose(cv::Mat::eye(4,4,CV_32F));
            cv::Mat Tcw = cv::Mat::eye(4,4,CV_32F);
            Rcw.copyTo(Tcw.rowRange(0,3).colRange(0,3));
            tcw.copyTo(Tcw.rowRange(0,3).col(3));
            mCurrentFrame.SetPose(Tcw);

            CreateInitialMapMonocular();
        }

以上程序的难点主要在于以下函数

//mvIniMatches:帧1特征点在帧2中的匹配
//Rcw,tcw:待求相机位姿
//mvIniP3D:成功匹配点的空间3D坐标
//vbTriangulated:成功三角测量--ture,三角测量失败--false
mpInitializer->Initialize(mCurrentFrame, mvIniMatches, Rcw, tcw, mvIniP3D, vbTriangulated)

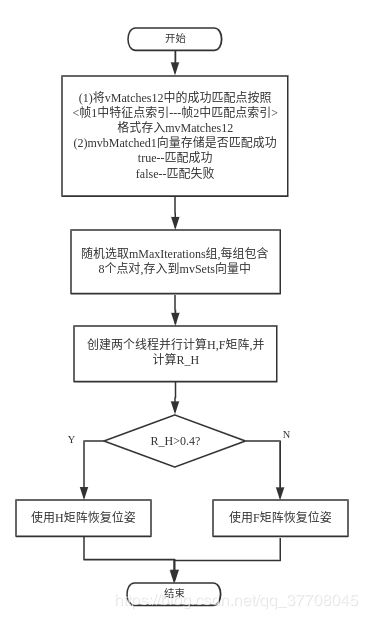
同样地,我们来看下这个函数的流程图.

  如下为创建组随机8点对的程序,如果大家没忘记的话,这不就是RANSAC随机采样一致性算法中的选取若干个最小子集?以下程序实现随机选取的思路大致如下:首先利用随机种子选择vAvailableIndices.size()范围内的一个索引值(vAvailableIndices.size()这玩意不就是成功匹配点的数量?),然后利用vAvailableIndices[randi] = vAvailableIndices.back()和 vAvailableIndices.pop_back();分别实现:将vAvailableIndices向量中的最后一位放置于已被抽选的索引值处;将vAvailableIndices向量中的最后一位删除.这样子就实现了vAvailableIndices向量一直保存为未抽取到的索引值,且向量大小逐渐减小.

    // Generate sets of 8 points for each RANSAC iteration
    //创建具有 mMaxIterations 个八点对向量的向量
    mvSets = vector< vector<size_t> >(mMaxIterations,vector<size_t>(8,0));

    DUtils::Random::SeedRandOnce(0);

    //随机选取 mMaxIterations 组,每组包含8个点,存入 mvSets 中
    for(int it=0; it<mMaxIterations; it++)
    {
        vAvailableIndices = vAllIndices;

        // Select a minimum set
        for(size_t j=0; j<8; j++)
        {
            int randi = DUtils::Random::RandomInt(0,vAvailableIndices.size()-1);
            int idx = vAvailableIndices[randi];

            mvSets[it][j] = idx;

            //删除已被选的索引
            vAvailableIndices[randi] = vAvailableIndices.back();
            vAvailableIndices.pop_back();
        }
    }

  选取好mMaxIterations组8点对之后,将创建两个临时线程,并行计算单应矩阵和基础矩阵,其中vbMatchesInliersH,SH,H为传入参数引用,目的是为了更新这两个值.

    // Launch threads to compute in parallel a fundamental matrix and a homography
    vector<bool> vbMatchesInliersH, vbMatchesInliersF;
    float SH, SF;
    cv::Mat H, F;

    thread threadH(&Initializer::FindHomography,this,ref(vbMatchesInliersH), ref(SH), ref(H));
    thread threadF(&Initializer::FindFundamental,this,ref(vbMatchesInliersF), ref(SF), ref(F));

    // Wait until both threads have finished
    threadH.join();
    threadF.join();

这里就稍微补充点C++知识吧,这是创建线程并启动线程的方式:

std::thread m_thrProcess(&类名::函数名, &类对象, 函数参数);

  至于为什么函数参数前面要加上ref()呢?std::ref只是尝试模拟引用传递，并不能真正变成引用，在非模板情况下，std::ref根本没法实现引用传递，只有模板自动推导类型时，ref能用包装类型reference_wrapper来代替原本会被识别的值类型，而reference_wrapper能隐式转换为被引用的值的引用类型。比如thread的方法传递引用的时候，必须外层用ref来进行引用传递，否则就是浅拷贝。而在下方添加threadH.join()时,所在线程将会被阻塞,直至线程完成,也就是说只有计算完H和F矩阵,程序才会运行后面的内容.

  言归正传,接下来让我们来看看FindHomography这个函数吧,至于FindFundamental这个函数,在这里笔者就不讲了,非常类似,在有了前面所讲的理论基础之后,相信同学们应该可以没什么障碍的读懂.

  进入FindHomography()函数,我们可以发现其中先将特征点进行归一化,再利用归一化后的坐标进行计算单应矩阵,而后再换算成原坐标的单应矩阵,至于为什么使用归一化的坐标呢?其实笔者也不是特别理解,希望路过的读者们谁知道的麻烦传授下笔者,感激不尽~~
归一化公式如下所示:
$$u^{{}^{\prime }}=\frac{u-u_{mean}}{{\sum }_{i=1}^N\left|u-u_{mean}\right|/N}\text{\hspace{1em}(1)}$$
$$v^{{}^{\prime }}=\frac{v-v_{mean}}{{\sum }_{i=1}^N\left|v-v_{mean}\right|/N}\text{\hspace{1em}(2)}$$
经过公式(1)和公式(2)的换算之后,就可以将原特征点的坐标归一化为均值为0,一阶绝对矩为1.令
$$sX=\sum _{i=1}^N\left|u-u_{mean}\right|/N$$
$$sY=\sum _{i=1}^N\left|v-v_{mean}\right|/N$$
可以得到原坐标和归一化坐标之间的归一化矩阵表示(归一化坐标=T*原坐标):
$$\left[\begin{array}{c}{u}^{{}^{\prime }}\\ v^{{}^{\prime }}\\ 1\end{array}\right]=\left[\begin{array}{ccc}sX& 0& -u_{mean}\cdot sX\\ 0& sY& -v_{mean}\cdot sY\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{c}(u-u_{mean})\cdot sX\\ (v-v_{mean})\cdot sY\\ 1\end{array}\right]\text{\hspace{1em}(3)}$$
由先前讲解的单应矩阵的计算可知:
$$p_2^{{}^{\prime }}=H_{21}^{{}^{\prime }}{p}_1^{{}^{\prime }}\text{\hspace{1em}(4)}$$
式(4)中使用的是皆为归一化的特征点坐标,求解出来的自然也是归一化后的单应矩阵,因此原坐标的单应矩阵计算公式如下:
$$T_2{p}_2=H_{21}^{{}^{\prime }}{T}_1{p}_1$$
其中$T_1$和$T_2$分别为帧1和帧2中对应的归一化矩阵.因此可得:
$$p_2=T_2^{-1}{H}_{21}^{{}^{\prime }}{T}_1{p}_1$$
故原坐标的单应矩阵为:
$$H_{21}=T_2^{-1}{H}_{21}^{{}^{\prime }}{T}_1\text{\hspace{1em}(5)}$$

  以下为核心代码,实现思路是使用mMaxIterations组随机八点对计算H矩阵,并调用 currentScore = CheckHomography(H21i, H12i, vbCurrentInliers, mSigma);函数计算该矩阵的分数,最后存储最高分数的单应矩阵作为最终结果.

    // Perform all RANSAC iterations and save the solution with highest score
    //从若干组解中寻找最优H
    for(int it=0; itscore)
        {
            H21 = H21i.clone();
            vbMatchesInliers = vbCurrentInliers;
            score = currentScore;
        }
    }

  其中ComputeH21()函数如下,如果大家还么忘记的话,应该知道最后算出来的解就是最小特征值对应的特征向量吧…emm…本来不想贴上这段代码的,没什么东西,不过主要是为了提醒大家这个点…

cv::Mat Initializer::ComputeH21(const vector<cv::Point2f> &vP1, const vector<cv::Point2f> &vP2)
{
    const int N = vP1.size();

    cv::Mat A(2*N,9,CV_32F);

    for(int i=0; i<N; i++)
    {
        const float u1 = vP1[i].x;
        const float v1 = vP1[i].y;
        const float u2 = vP2[i].x;
        const float v2 = vP2[i].y;

        //为啥v2  取了相反数(虽然好像无所谓)
        A.at<float>(2*i,0) = 0.0;
        A.at<float>(2*i,1) = 0.0;
        A.at<float>(2*i,2) = 0.0;
        A.at<float>(2*i,3) = -u1;
        A.at<float>(2*i,4) = -v1;
        A.at<float>(2*i,5) = -1;
        A.at<float>(2*i,6) = v2*u1;
        A.at<float>(2*i,7) = v2*v1;
        A.at<float>(2*i,8) = v2;

        A.at<float>(2*i+1,0) = u1;
        A.at<float>(2*i+1,1) = v1;
        A.at<float>(2*i+1,2) = 1;
        A.at<float>(2*i+1,3) = 0.0;
        A.at<float>(2*i+1,4) = 0.0;
        A.at<float>(2*i+1,5) = 0.0;
        A.at<float>(2*i+1,6) = -u2*u1;
        A.at<float>(2*i+1,7) = -u2*v1;
        A.at<float>(2*i+1,8) = -u2;

    }
    cv::Mat u,w,vt;

    //A=U*W*Vt
    cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);

    return vt.row(8).reshape(0, 3);
}

  接下来我们来看看currentScore = CheckHomography(H21i, H12i, vbCurrentInliers, mSigma);函数的细节吧,orbslam2中采用了双向重投影误差,计算公式如下:
$$score=\sum _{i=1}^N(2\cdot th-\frac{{\Vert \begin{array}{c}{p}_2^1-p_1^1\end{array}\Vert }^2+{\Vert \begin{array}{c}{p}_2^2-p_1^2\end{array}\Vert }^2}{{\sigma }^2})$$
$$\begin{gathered} if\frac{{\Vert \begin{array}{c}{p}_2-p_1\end{array}\Vert }^2}{{\sigma }^2}\le th \\ then,该点为inlines,否则为outliners且不算入上述score计算 \end{gathered}$$
其中,$p_2^1$表示帧2中的匹配点经过H矩阵投影在帧1中的点,$p_1^1$表示帧1中的原特征点,以此类推.实现代码如下:

/** 利用H矩阵计算reprojection error 
    score=the sum of all matches(2*th-(||p2-p1||^2+ ||p1-p2||^2)/sigma^2)
    if ||p2-p1||^2/sigma^2 or ||p1-p2||^2/sigma^2 > th
    then set the point outliners
    return score
**/
float Initializer::CheckHomography(const cv::Mat &H21, const cv::Mat &H12, vector<bool> &vbMatchesInliers, float sigma)
{   
    const int N = mvMatches12.size();

    const float h11 = H21.at<float>(0,0);
    const float h12 = H21.at<float>(0,1);
    const float h13 = H21.at<float>(0,2);
    const float h21 = H21.at<float>(1,0);
    const float h22 = H21.at<float>(1,1);
    const float h23 = H21.at<float>(1,2);
    const float h31 = H21.at<float>(2,0);
    const float h32 = H21.at<float>(2,1);
    const float h33 = H21.at<float>(2,2);

    const float h11inv = H12.at<float>(0,0);
    const float h12inv = H12.at<float>(0,1);
    const float h13inv = H12.at<float>(0,2);
    const float h21inv = H12.at<float>(1,0);
    const float h22inv = H12.at<float>(1,1);
    const float h23inv = H12.at<float>(1,2);
    const float h31inv = H12.at<float>(2,0);
    const float h32inv = H12.at<float>(2,1);
    const float h33inv = H12.at<float>(2,2);

    vbMatchesInliers.resize(N);

    float score = 0;

    const float th = 5.991;

    const float invSigmaSquare = 1.0/(sigma*sigma);

    for(int i=0; i<N; i++)
    {
        bool bIn = true;

        const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
        const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];

        const float u1 = kp1.pt.x;
        const float v1 = kp1.pt.y;
        const float u2 = kp2.pt.x;
        const float v2 = kp2.pt.y;

        // Reprojection error in first image
        // x2in1 = H12*x2

        const float w2in1inv = 1.0/(h31inv*u2+h32inv*v2+h33inv);
        const float u2in1 = (h11inv*u2+h12inv*v2+h13inv)*w2in1inv;
        const float v2in1 = (h21inv*u2+h22inv*v2+h23inv)*w2in1inv;

        const float squareDist1 = (u1-u2in1)*(u1-u2in1)+(v1-v2in1)*(v1-v2in1);//2范数的平方

        const float chiSquare1 = squareDist1*invSigmaSquare;

        if(chiSquare1>th)
            bIn = false;
        else
            score += th - chiSquare1;

        // Reprojection error in second image
        // x1in2 = H21*x1

        const float w1in2inv = 1.0/(h31*u1+h32*v1+h33);
        const float u1in2 = (h11*u1+h12*v1+h13)*w1in2inv;
        const float v1in2 = (h21*u1+h22*v1+h23)*w1in2inv;

        const float squareDist2 = (u2-u1in2)*(u2-u1in2)+(v2-v1in2)*(v2-v1in2);

        const float chiSquare2 = squareDist2*invSigmaSquare;

        if(chiSquare2>th)
            bIn = false;
        else
            score += th - chiSquare2;

        if(bIn)
            vbMatchesInliers[i]=true;
        else
            vbMatchesInliers[i]=false;
    }

    return score;
}

至于基础矩阵F的求解过程与单应矩阵求解类似,主要说说两者之间的不同.

1. 单应矩阵由于投影过去是一个点,所以双向重投影误差算的是两点之间的距离,而基础矩阵一个点投影过去得到是一条极线,因此双向重投影误差算的是点到线之间的距离.
2. 单应矩阵的th是5.991,而基础矩阵的th是3.841,但是最终在计算分数时都是统一使用5.991,这当然是为了让结果有可比性.
3. 由于基础矩阵具有特征值为:$[\sigma ,\sigma ,0{]}^T$的内在性质,所以计算出来的F矩阵会进行奇异值分解,并且调整特征值的大小,源码中是直接让最后一位奇异值为0,虽然也可以这样$[\frac{{\sigma }_1+{\sigma }_2}{2},\frac{{\sigma }_1+{\sigma }_2}{2},0{]}^T$
4. 基础矩阵的分数计算公式:
   $$score=\sum _{i=1}^N(2\cdot th-\frac{{\Vert \begin{array}{c}\frac{a_2{u}_2+b_2{v}_2+c_2}{\sqrt{a_2^2+b_2^2}}\end{array}\Vert }^2+{\Vert \begin{array}{c}\frac{a_1{u}_1+b_1{v}_1+c_1}{\sqrt{a_1^2+b_1^2}}\end{array}\Vert }^2}{{\sigma }^2})$$

其中${\Vert \begin{array}{c}\frac{a_1{u}_1+b_1{v}_1+c_1}{\sqrt{a_1^2+b_1^2}}\end{array}\Vert }^2$不正是点到线距离的计算公式么?第四点的分数部分计算源码如下:

        const float u1 = kp1.pt.x;
        const float v1 = kp1.pt.y;
        const float u2 = kp2.pt.x;
        const float v2 = kp2.pt.y;

        // Reprojection error in second image
        // l2=F21x1=(a2,b2,c2)

        const float a2 = f11*u1+f12*v1+f13;
        const float b2 = f21*u1+f22*v1+f23;
        const float c2 = f31*u1+f32*v1+f33;

        const float num2 = a2*u2+b2*v2+c2;

        const float squareDist1 = num2*num2/(a2*a2+b2*b2);//p2点到直线F21*p1的距离的平方

至此,我们已经讲解完单目初始化的绝大部分内容,除了初始地图构建,关键帧插入,该部分内容留到下章继续讲解~~

---

总结

1. 该章节主要是对源码进行解说,其中包括:F矩阵的求解,H矩阵的求解
2. RANSAC随机采样一致性算法源码实现
3. score计算方式源码实现

参考文献:

1. ORB-SLAM a Versatile and Accurate Monocular SLAM System
2. 高翔–视觉SLAM十四讲
3. 吴博-ORB-SLAM代码详细解读
4. 其他博主的文章:https://blog.csdn.net/hzwwpgmwy/article/details/83578694

PS:

1. 如果您觉得我的博客对您有所帮助，欢迎关注我的博客。此外，欢迎转载我的文章，但请注明出处链接。
2. 本博客仅代表个人观点,不一定完全正确,如有出错之处,也欢迎批评指正.
   

 
 
上一章节:一步步带你看懂orbslam2源码–单应矩阵/基础矩阵,求解R,t(四)
下一章节:一步步带你看懂orbslam2源码–地图初始化\关键帧插入(六)–待更新…