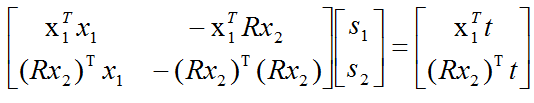第十二讲 单目稠密重建

#include 
#include 
#include 
using namespace std;
#include 

// for sophus
#include  //这里使用了sophus这个工具，使用SE3
using Sophus::SE3;

// for eigen
#include 
#include 
using namespace Eigen;

#include 
#include 
#include 

using namespace cv;
// ------------------------------------------------------------------
// parameters
const int boarder = 20;     // 边缘宽度
const int width = 640;      // 宽度
const int height = 480;     // 高度
const double fx = 481.2f;   // 相机内参
const double fy = -480.0f;
const double cx = 319.5f;
const double cy = 239.5f;
const int ncc_window_size = 2;  // NCC 取的窗口半宽度
const int ncc_area = (2*ncc_window_size+1)*(2*ncc_window_size+1); // NCC窗口面积
const double min_cov = 0.1; // 收敛判定：最小方差
const double max_cov = 10;  // 发散判定：最大方差

// ------------------------------------------------------------------
// 重要的函数
// 从 REMODE 数据集读取数据
bool readDatasetFiles(
    const string& path,
    vector<string>& color_image_files,
    vector& poses
)；
// 根据新的图像更新深度估计
bool update(
    const Mat& ref,
    const Mat& curr,
    const SE3& T_C_R,
    Mat& depth,
    Mat& depth_cov
);
// 极线搜索
bool epipolarSearch(
    const Mat& ref,
    const Mat& curr,
    const SE3& T_C_R,
    const Vector2d& pt_ref,
    const double& depth_mu,
    const double& depth_cov,
    Vector2d& pt_curr
);
// 更新深度滤波器
bool updateDepthFilter(
    const Vector2d& pt_ref,
    const Vector2d& pt_curr,
    const SE3& T_C_R,
    Mat& depth,
    Mat& depth_cov
);
// 计算 NCC 评分
double NCC( const Mat& ref, const Mat& curr, const Vector2d& pt_ref, const Vector2d& pt_curr );
// 双线性灰度插值
inline double getBilinearInterpolatedValue( const Mat& img, const Vector2d& pt ) {
    uchar* d = & img.data[ int(pt(1,0))*img.step+int(pt(0,0)) ];
    double xx = pt(0,0) - floor(pt(0,0));
    double yy = pt(1,0) - floor(pt(1,0));
    return  (( 1-xx ) * ( 1-yy ) * double(d[0]) +
            xx* ( 1-yy ) * double(d[1]) +
            ( 1-xx ) *yy* double(d[img.step]) +
            xx*yy*double(d[img.step+1]))/255.0;
}

// ------------------------------------------------------------------
// 一些小工具
// 显示估计的深度图
bool plotDepth( const Mat& depth );
// 像素到相机坐标系
inline Vector3d px2cam ( const Vector2d px ) {
    return Vector3d (
        (px(0,0) - cx)/fx,
        (px(1,0) - cy)/fy,
        1
    );
}
// 相机坐标系到像素
inline Vector2d cam2px ( const Vector3d p_cam ) {
    return Vector2d (
        p_cam(0,0)*fx/p_cam(2,0) + cx,
        p_cam(1,0)*fy/p_cam(2,0) + cy
    );
}
// 检测一个点是否在图像边框内
inline bool inside( const Vector2d& pt ) {
    return pt(0,0) >= boarder && pt(1,0)>=boarder
        && pt(0,0)+boarder1,0)+boarder<=height;
}
// 显示极线匹配
void showEpipolarMatch( const Mat& ref, const Mat& curr, const Vector2d& px_ref, const Vector2d& px_curr );
// 显示极线
void showEpipolarLine( const Mat& ref, const Mat& curr, const Vector2d& px_ref, const Vector2d& px_min_curr, const Vector2d& px_max_curr );
// ------------------------------------------------------------------
int main( int argc, char** argv )
{
    // 从数据集读取数据
    vector<string> color_image_files;
    vector poses_TWC;
    //该函数的功能是将图片名和位姿从文件中提取出来并进行存储
    //其中“/home/.../data”是存放文件的路径
    bool ret = readDatasetFiles(“/home/.../data”, color_image_files, poses_TWC );
    if ( ret==false )
    {
        cout<<"Reading image files failed!"<return -1;
    }
    cout<<"read total "<" files."<// 第一张图
    Mat ref = imread( color_image_files[0], 0 );               // gray-scale image
    SE3 pose_ref_TWC = poses_TWC[0];
    double init_depth   = 3.0;    // 深度初始值
    double init_cov2    = 3.0;    // 方差初始值
    Mat depth( height, width, CV_64F, init_depth );             // 深度图
    Mat depth_cov( height, width, CV_64F, init_cov2 );          // 深度图方差

    for ( int index=1; indexcout<<"*** loop "<" ***"<0 );
        if (curr.data == nullptr) continue;
        SE3 pose_curr_TWC = poses_TWC[index];
        SE3 pose_T_C_R = pose_curr_TWC.inverse() * pose_ref_TWC; // 坐标转换关系： T_C_W * T_W_R = T_C_R
        update( ref, curr, pose_T_C_R, depth, depth_cov );
        plotDepth( depth );
        imshow("image", curr);
        waitKey(1);
    }

    cout<<"estimation returns, saving depth map ..."<"depth.png", depth );
    cout<<"done."<return 0;
}

bool readDatasetFiles(
    const string& path,
    vector< string >& color_image_files,
    std::vector& poses
)
{
    ifstream fin( path+"/first_200_frames_traj_over_table_input_sequence.txt");
    if ( !fin ) return false;
    while ( !fin.eof() )
    {
    // 数据格式：图像文件名 tx, ty, tz, qx, qy, qz, qw ，注意是 TWC 而非 TCW
        string image;
        fin>>image;
        double data[7];//大小为7，0-6
        for ( double& d:data ) fin>>d;//用for auto 遍历data并复制给d

        color_image_files.push_back( path+string("/images/")+image );
        poses.push_back(
            SE3( Quaterniond(data[6], data[3], data[4], data[5]),
                 Vector3d(data[0], data[1], data[2]))
        );
        if ( !fin.good() ) break;
    }
    return true;
}

// 对整个深度图进行更新
bool update(const Mat& ref, const Mat& curr, const SE3& T_C_R, Mat& depth, Mat& depth_cov )
{
#pragma omp parallel for
    for ( int x=boarder; x从边界开始到小于宽度减去边界
#pragma omp parallel for
        for ( int y=boarder; y// 遍历每个像素
            if ( depth_cov.ptr<double>(y)[x] < min_cov || depth_cov.ptr<double>(y)[x] > max_cov ) //min_cov，max_cov 收敛和发散判定最上面定义的 深度已收敛或发散
                continue;
            // 在极线上搜索 (x,y) 的匹配
            Vector2d pt_curr;
            bool ret = epipolarSearch (
                ref,
                curr,
                T_C_R,
                Vector2d(x,y),
                depth.ptr<double>(y)[x],
                sqrt(depth_cov.ptr<double>(y)[x]),//sqrt平方根
                pt_curr
            );

            if ( ret == false ) // 匹配失败
                continue;

      // 取消该注释以显示匹配
            // showEpipolarMatch( ref, curr, Vector2d(x,y), pt_curr );

            // 匹配成功，更新深度图
            updateDepthFilter( Vector2d(x,y), pt_curr, T_C_R, depth, depth_cov );
        }
}

// 极线搜索
bool epipolarSearch(
    const Mat& ref, const Mat& curr,
    const SE3& T_C_R, const Vector2d& pt_ref,
    const double& depth_mu, const double& depth_cov,
    Vector2d& pt_curr )
{
    Vector3d f_ref = px2cam( pt_ref );//像素坐标系到相机坐标系
    f_ref.normalize();//归一化
    Vector3d P_ref = f_ref*depth_mu;    // 参考帧的 P 向量(p的相机坐标）,depth_mu?????
//T_C_R参考帧到当前帧，T_R_C当前帧到参考帧
    Vector2d px_mean_curr = cam2px( T_C_R*P_ref ); // 按深度均值投影的像素，p的相机坐标经过位姿变换投影到第二帧像素坐标系
    double d_min = depth_mu-3*depth_cov, d_max = depth_mu+3*depth_cov;//depth从文件读进来的
    if ( d_min<0.1 ) d_min = 0.1;
    Vector2d px_min_curr = cam2px( T_C_R*(f_ref*d_min) );   // 按最小深度投影的像素
    Vector2d px_max_curr = cam2px( T_C_R*(f_ref*d_max) );   // 按最大深度投影的像素

    Vector2d epipolar_line = px_max_curr - px_min_curr; // 极线（线段形式）
    Vector2d epipolar_direction = epipolar_line;        // 极线方向
    epipolar_direction.normalize();
    double half_length = 0.5*epipolar_line.norm();  // 极线线段的半长度
    if ( half_length>100 ) half_length = 100;   // 我们不希望搜索太多东西

  // 取消此句注释以显示极线（线段）
    // showEpipolarLine( ref, curr, pt_ref, px_min_curr, px_max_curr );

    // 在极线上搜索，以深度均值点为中心，左右各取半长度
    double best_ncc = -1.0;
    Vector2d best_px_curr;
    for ( double l=-half_length; l<=half_length; l+=0.7 )  // l+=sqrt(2)
    {
        Vector2d px_curr = px_mean_curr + l*epipolar_direction;  // 待匹配点
        if ( !inside(px_curr) )
            continue;
        // 计算待匹配点与参考帧的 NCC
        double ncc = NCC( ref, curr, pt_ref, px_curr );
        if ( ncc>best_ncc )
        {
            best_ncc = ncc;
            best_px_curr = px_curr;
        }
    }
    if ( best_ncc < 0.85f )      // 只相信 NCC 很高的匹配
        return false;
    pt_curr = best_px_curr;
    return true;
}

double NCC (
    const Mat& ref, const Mat& curr,
    const Vector2d& pt_ref, const Vector2d& pt_curr
)
{
    // 零均值-归一化互相关
    // 先算均值
    double mean_ref = 0, mean_curr = 0;
    vector<double> values_ref, values_curr; // 参考帧和当前帧的均值
    for ( int x=-ncc_window_size; x<=ncc_window_size; x++ )
        for ( int y=-ncc_window_size; y<=ncc_window_size; y++ )
        {//pt_ref(1,0)为y,pt_ref(0,0)为X
            double value_ref = double(ref.ptr( int(y+pt_ref(1,0)) )[ int(x+pt_ref(0,0)) ])/255.0;
            mean_ref += value_ref;

            double value_curr = getBilinearInterpolatedValue( curr, pt_curr+Vector2d(x,y) );//双线性灰度插值
            mean_curr += value_curr;

            values_ref.push_back(value_ref);
            values_curr.push_back(value_curr);
        }

    mean_ref /= ncc_area;
    mean_curr /= ncc_area;

  // 计算 Zero mean NCC
    double numerator = 0, demoniator1 = 0, demoniator2 = 0;
    for ( int i=0; idouble n = (values_ref[i]-mean_ref) * (values_curr[i]-mean_curr);
        numerator += n;
        demoniator1 += (values_ref[i]-mean_ref)*(values_ref[i]-mean_ref);
        demoniator2 += (values_curr[i]-mean_curr)*(values_curr[i]-mean_curr);
    }
    return numerator / sqrt( demoniator1*demoniator2+1e-10 );   // 防止分母出现零
}

bool updateDepthFilter(
    const Vector2d& pt_ref,
    const Vector2d& pt_curr,
    const SE3& T_C_R,
    Mat& depth,
    Mat& depth_cov
)
{
    // 我是一只喵
    // 不知道这段还有没有人看
    // 用三角化计算深度
    SE3 T_R_C = T_C_R.inverse();//正交矩阵转置等于逆
    Vector3d f_ref = px2cam( pt_ref );
    f_ref.normalize();
    Vector3d f_curr = px2cam( pt_curr );
    f_curr.normalize();

    // 方程
    // d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC  s1*x1=s2*(R*x2+t)   // => [ f_ref^T f_ref, -f_ref^T f_cur ] [d_ref] = [f_ref^T t]    //    [ f_cur^T f_ref, -f_cur^T f_cur ] [d_cur] = [f_cur^T t]

三角化公式

按照对极几何中的定义，设x₁, x₂为两个特征点的归一化坐标，则它们满足：

s₁x₁ = s₂Rx₂ + t                                                                公式(1)

=> s₁x₁ - s₂Rx₂ = t                                                            公式(2)

对公式(2)左右两侧分别乘以x_1^T，得：

s₁x₁^Tx₁ - s₂x₁^TRx₂ = x₁^T t                                                  公式(3)

对公式(2)左右两侧分别乘以(Rx₂)^_T，得：

s₁(Rx₂)^Tx₁ - s₂(Rx₂)^TRx₂ = (Rx₂)^T t                                     公式(4)

由公式(3)和公式(4)可以联立得到一个一元二次线性方程组，然后可以利用Cramer‘s法则（参见线性代数书）进行求解。

x1=f_ref x2=f_cur s1=d_ref s2=d_cur // 二阶方程用克莱默法则求解并解之 Vector3d t = T_R_C.translation(); Vector3d f2 = T_R_C.rotation_matrix() * f_curr; Vector2d b = Vector2d ( t.dot ( f_ref ), t.dot ( f2 ) );// 例如Vector3d v(1, 2, 3); Vector3d w(0, 1, 2); 那么v.dot(w) 得到的结果是8 double A[4]; A[ 0] = f_ref.dot ( f_ref ); A[ 2] = f_ref.dot ( f2 ); A[ 1] = -A[ 2]; A[ 3] = - f2.dot ( f2 ); double d = A[ 0]*A[ 3]-A[ 1]*A[ 2];// 行列式的值 Vector2d lambdavec = Vector2d ( A[ 3] * b ( 0, 0 ) - A[ 1] * b ( 1, 0 ), -A[ 2] * b ( 0, 0 ) + A[ 0] * b ( 1, 0 )) /d;// A*b/d Vector3d xm = lambdavec ( 0, 0 ) * f_ref; Vector3d xn = t + lambdavec ( 1, 0 ) * f2; Vector3d d_esti = ( xm+xn ) / 2.0; // 三角化算得的深度向量 double depth_estimation = d_esti.norm(); // 深度值 // 计算不确定性（以一个像素为误差）p326公式 Vector3d p = f_ref*depth_estimation; Vector3d a = p - t; double t_norm = t.norm(); double a_norm = a.norm(); double alpha = acos( f_ref.dot(t)/t_norm ); double beta = acos( -a.dot(t)/(a_norm*t_norm)); double beta_prime = beta + atan( 1/fx); double gamma = M_PI - alpha - beta_prime; double p_prime = t_norm * sin(beta_prime) / sin(gamma); double d_cov = p_prime - depth_estimation; double d_cov2 = d_cov*d_cov; // 高斯融合 double mu = depth.ptr< double>( int(pt_ref( 1, 0)) )[ int(pt_ref( 0, 0)) ];//已有的 double sigma2 = depth_cov.ptr< double>( int(pt_ref( 1, 0)) )[ int(pt_ref( 0, 0)) ];//跟新的 double mu_fuse = (d_cov2*mu+sigma2*depth_estimation) / ( sigma2+d_cov2);//式16.3 double sigma_fuse2 = ( sigma2 * d_cov2 ) / ( sigma2 + d_cov2 ); depth.ptr< double>( int(pt_ref( 1, 0)) )[ int(pt_ref( 0, 0)) ] = mu_fuse;//更新 depth_cov.ptr< double>( int(pt_ref( 1, 0)) )[ int(pt_ref( 0, 0)) ] = sigma_fuse2; return true; } bool plotDepth( const Mat& depth) { imshow( "depth", depth* 0.4 ); waitKey( 1); } void showEpipolarMatch(const Mat& ref, const Mat& curr, const Vector2d& px_ref, const Vector2d& px_curr) {     Mat ref_show, curr_show;     cv::cvtColor( ref, ref_show, CV_GRAY2BGR );     cv::cvtColor( curr, curr_show, CV_GRAY2BGR );          cv::circle( ref_show, cv::Point2f(px_ref(0,0), px_ref(1,0)), 5, cv::Scalar(0,0,250), 2);     cv::circle( curr_show, cv::Point2f(px_curr(0,0), px_curr(1,0)), 5, cv::Scalar(0,0,250), 2);          imshow("ref", ref_show );     imshow("curr", curr_show );     waitKey(1); } void showEpipolarLine(const Mat& ref, const Mat& curr, const Vector2d& px_ref, const Vector2d& px_min_curr, const Vector2d& px_max_curr) {     Mat ref_show, curr_show;     cv::cvtColor( ref, ref_show, CV_GRAY2BGR );     cv::cvtColor( curr, curr_show, CV_GRAY2BGR );          cv::circle( ref_show, cv::Point2f(px_ref(0,0), px_ref(1,0)), 5, cv::Scalar(0,255,0), 2);     cv::circle( curr_show, cv::Point2f(px_min_curr(0,0), px_min_curr(1,0)), 5, cv::Scalar(0,255,0), 2);     cv::circle( curr_show, cv::Point2f(px_max_curr(0,0), px_max_curr(1,0)), 5, cv::Scalar(0,255,0), 2);     cv::line( curr_show, Point2f(px_min_curr(0,0), px_min_curr(1,0)), Point2f(px_max_curr(0,0), px_max_curr(1,0)), Scalar(0,255,0), 1);          imshow("ref", ref_show );     imshow("curr", curr_show );     waitKey(1); }

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83
• 84
• 85
• 86
• 87
• 88
• 89
• 90
• 91
• 92
• 93
• 94
• 95
• 96
• 97
• 98
• 99
• 100
• 101
• 102
• 103
• 104
• 105
• 106
• 107
• 108
• 109
• 110
• 111
• 112
• 113
• 114
• 115
• 116
• 117
• 118
• 119
• 120
• 121
• 122
• 123
• 124
• 125
• 126
• 127
• 128
• 129
• 130
• 131
• 132
• 133
• 134
• 135
• 136
• 137
• 138
• 139
• 140
• 141
• 142
• 143
• 144
• 145
• 146
• 147
• 148
• 149
• 150
• 151
• 152
• 153
• 154
• 155
• 156
• 157
• 158
• 159
• 160
• 161
• 162
• 163
• 164
• 165
• 166
• 167
• 168
• 169
• 170
• 171
• 172
• 173
• 174
• 175
• 176
• 177
• 178
• 179
• 180
• 181
• 182
• 183
• 184
• 185
• 186
• 187
• 188
• 189
• 190
• 191
• 192
• 193
• 194
• 195
• 196
• 197
• 198
• 199
• 200
• 201
• 202
• 203
• 204
• 205
• 206
• 207
• 208
• 209
• 210
• 211
• 212
• 213
• 214
• 215
• 216
• 217
• 218
• 219
• 220
• 221
• 222
• 223
• 224
• 225
• 226
• 227
• 228
• 229
• 230
• 231
• 232
• 233
• 234
• 235
• 236
• 237
• 238
• 239
• 240
• 241
• 242
• 243
• 244
• 245
• 246
• 247
• 248
• 249
• 250
• 251
• 252
• 253
• 254
• 255
• 256
• 257
• 258
• 259
• 260
• 261
• 262
• 263
• 264
• 265
• 266
• 267
• 268
• 269
• 270
• 271
• 272
• 273
• 274
• 275
• 276
• 277
• 278
• 279
• 280
• 281
• 282
• 283
• 284
• 285
• 286
• 287
• 288
• 289
• 290
• 291
• 292
• 293
• 294
• 295
• 296
• 297
• 298
• 299
• 300
• 301
• 302
• 303
• 304
• 305
• 306
• 307
• 308
• 309
• 310
• 311
• 312
• 313
• 314
• 315
• 316
• 317
• 318
• 319
• 320
• 321
• 322
• 323
• 324
• 325
• 326
• 327
• 328
• 329
• 330
• 331
• 332
• 333
• 334
• 335
• 336
• 337
• 338
• 339
• 340
• 341
• 342
• 343
• 344
• 345
• 346
• 347
• 348
• 349
• 350
• 351
• 352
• 353
• 354
• 355
• 356
• 357
• 358
• 359
• 360
• 361
• 362
• 363
• 364
• 365
• 366
• 367