2020牛客寒假算法基础集训营1 解题报告 Apare_xzc
2020牛客寒假算法基础集训营1 解题报告 Apare_xzc
比赛链接：2020牛客寒假算法基础集训营1<–
2020-02-04 13:00:00 至 2020-02-04 18:00:00
时长: 5小时
已有3952人报名
官方题解：【题解】牛客寒假集训营第一场 <–
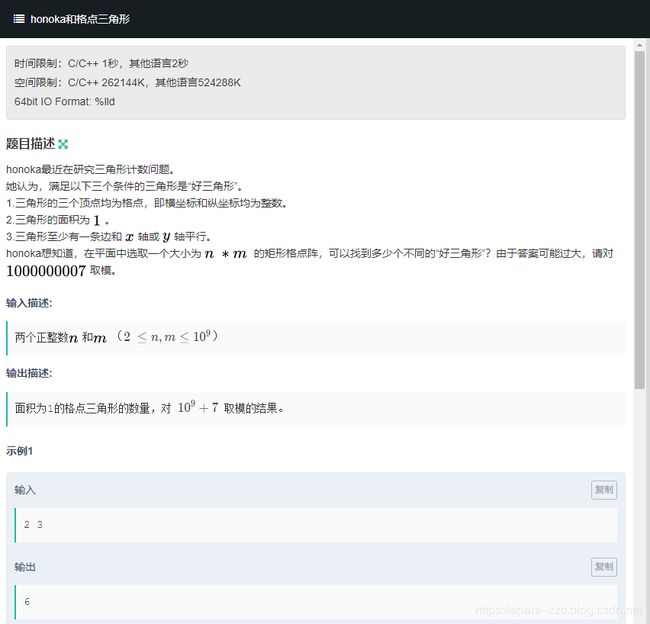
A. honoka和格点三角形
题目链接
分析：
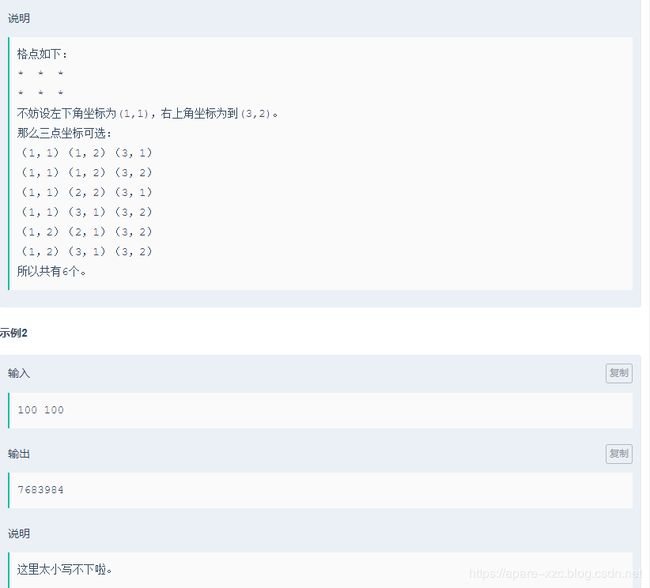
求格点内能连成的面积为1的三角形的个数，要求三角形至少有一条边与x轴或y轴平行。
满足条件的三角形的总数ans = 有一条边与x轴平行的三角形个数 ans1 有一条边与y轴平行的三角形的个数 ans2 - 直角三角形的个数ans3
计算的方法都相同，以平行于x轴的三角形为例。三角形面积为1，一定是底为1高为2，或者底为2，高为1。那么必然有两个点的纵坐标相同，他们在纵坐标一定的时候，横坐标的范围是1到m, 于是底为1的两点有m-1种取法，每种取法可以改变纵坐标，上下移动，可知横坐标确定了的有一边平行于x轴的三角形第三个点的纵坐标有(n-2)*2种，纵坐标确定之后，三角形的高确定，第三个点有m中取法(直角三角形有2种)。
其它的情况都类似，互换m,n即可。具体公式见代码。
我的代码：
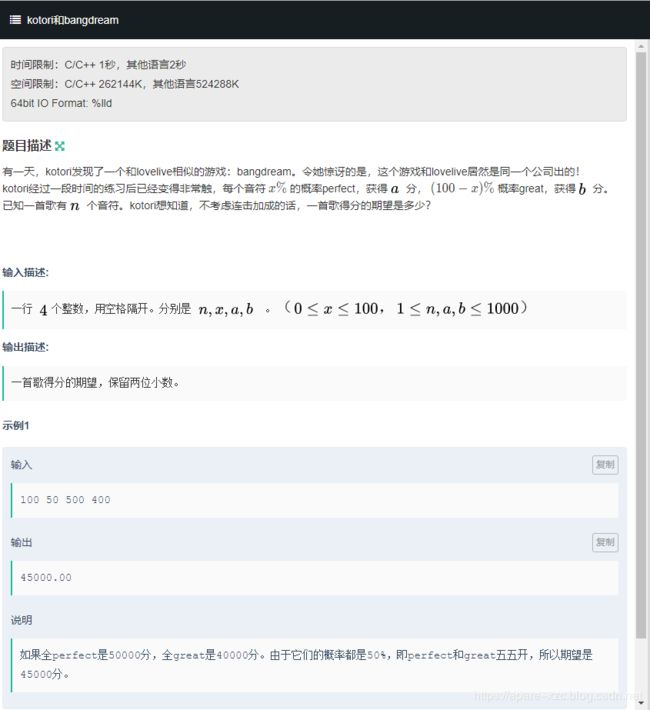
#include 
B. kotori和bangdream
题目链接
分析：
签到题，期望 = 1.0xa/100 1.0b(100-x)/100*n
代码
#include C. umi和弓道
题目链接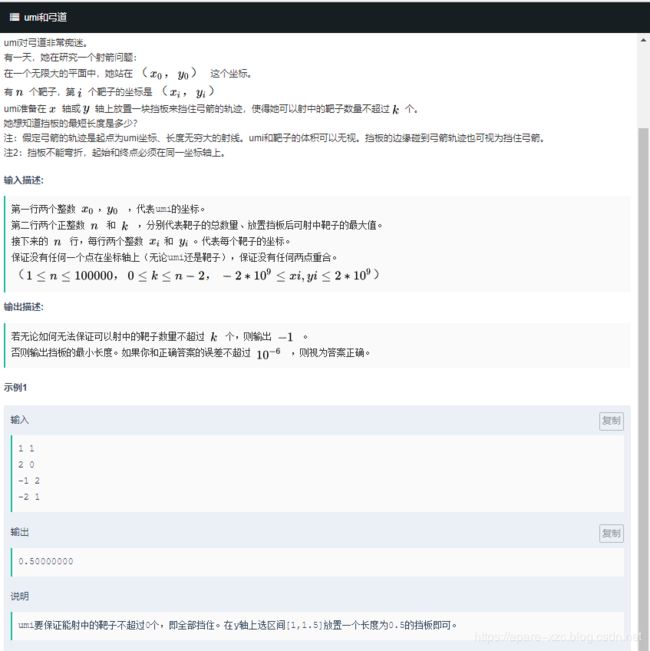 
不想写计算几何，这题没写，跳过吧…
D. hanayo和米饭
题目链接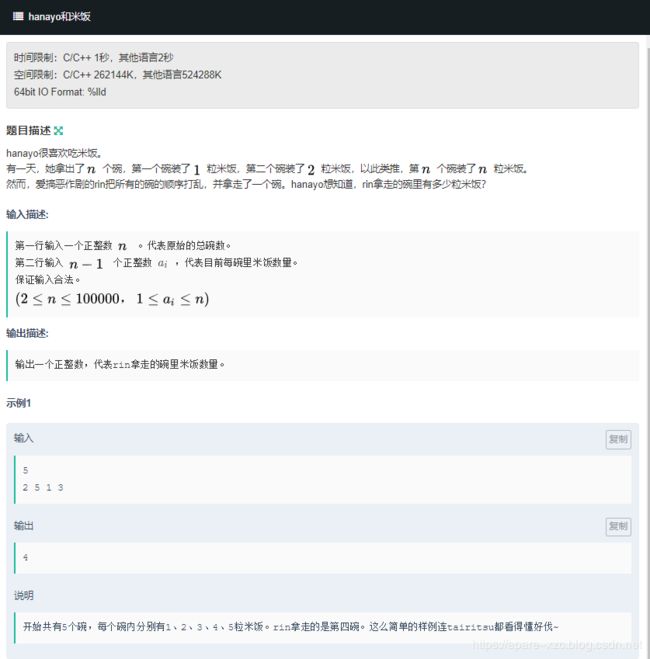 
分析：
1到n的数列少了一个，给n-1个，求少的那一个。直接 (1 n)*n/2 - sum(arr) 即可。用n个数的和减去n-1个数的和
#include E. rin和快速迭代
题目链接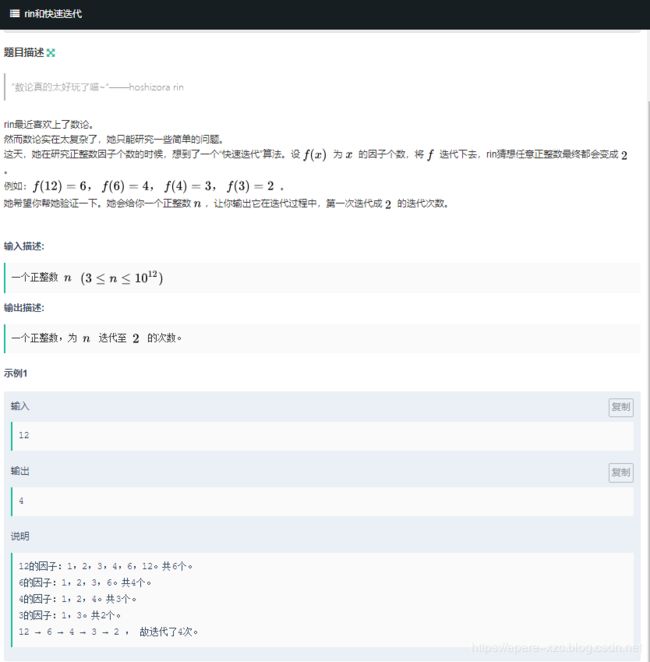
分析：
也没有找到什么规律或者公式。那就按题意模拟吧。我们只需要进行迭代，每次用f(x)代替x，直到x变为2。求迭代了多少次。如何求x因数的个数呢？我们先对x进行分解质因数，得到
x = P1^C1 * P2^C2 * ... * Pk^Ck
其中P1,P2...Pk均为质数
那么每个质因数Pi的次数可以选{0,1,2…Ci}，共有Ci 1种选法，那么根据乘法原理，因数的个数就是Ci 1的乘积。
我们可以先筛出1E6之内的质数，加快分解因式的速度。
我用的是欧拉线性筛，复杂度为O(n), 分解质因数的复杂度大约为根号n
我的代码
#include F. maki和tree
题目链接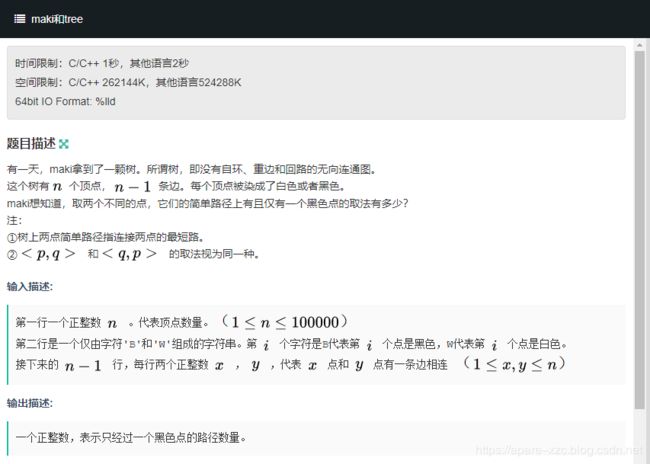 
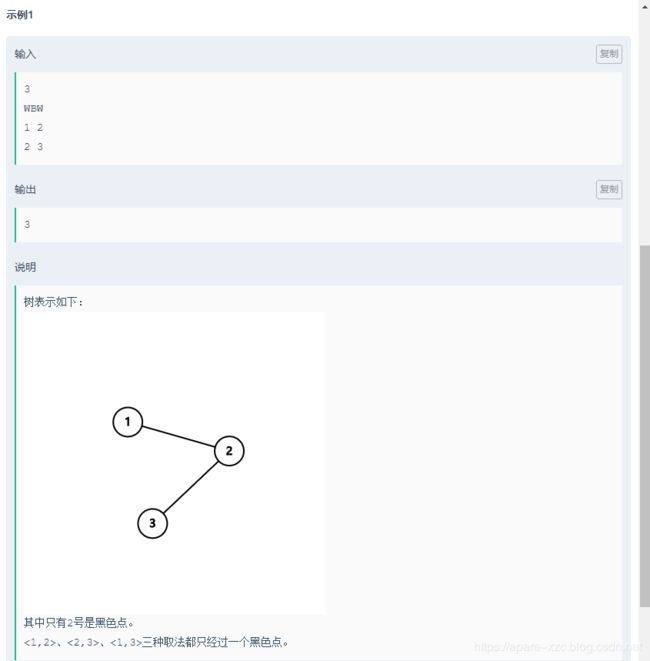
分析：
求树上两点间路径只有一个黑色节点的对数。我们只需要对每一个黑色节点dfs，求出包含该黑色节点的路径数(点的对数)相加即可。
每个黑节点有若干个白色节点与之相连，相互不经过黑色节点可达的白色节点看成是一个连通的整体，我们dfs求出这些连通的整体中白色节点的个数，记录这些个数v0,v1,v2… 可以存在一个vector之中。那么，如果黑色节点是点对两点中的某一点，路径的数目为v0,v1,v2…之和，也就是黑色节点不经过其它黑色节点可达的白色节点的个数之和。如果黑色节点不是点对中的某一点，那么两个点一定在不同的连通整体中，这样的路径数位v0,v1,v2… 这些数两两相乘相加之和。
我的代码：
#include G. eli和字符串
题目链接 
分析：
我们可以每个小写字母开一个vector，记录该字母在字符串中出现的所有位置，是一个递增的序列。然后我们每个字母从v[i]开始，v[i k-1]结束的这一段含有k个相同的字母，用v[i k-1] - v[i] 1更新答案即可
我的代码：
#include H. nozomi和字符串
题目链接
分析：
在K次操作之内，求最大的数字相同的子串的长度。数字都相同，无非只有两种情况，一种是全部为0，一种是全部为1。
我们可以二分答案，枚举子串的起点，二分子串的长度。如果是全1串，我们需要求得串中0的个数，来判断是否能在K次操作之内都变为1。我们可以维护一个0的个数的前缀和(1同理) ，于是我们可以O(1)check。起点一定的话，0或1的个数也随着长度的增加单调非递减，满足二分的性质。
我的代码：
#include I. nico和niconiconi
题目链接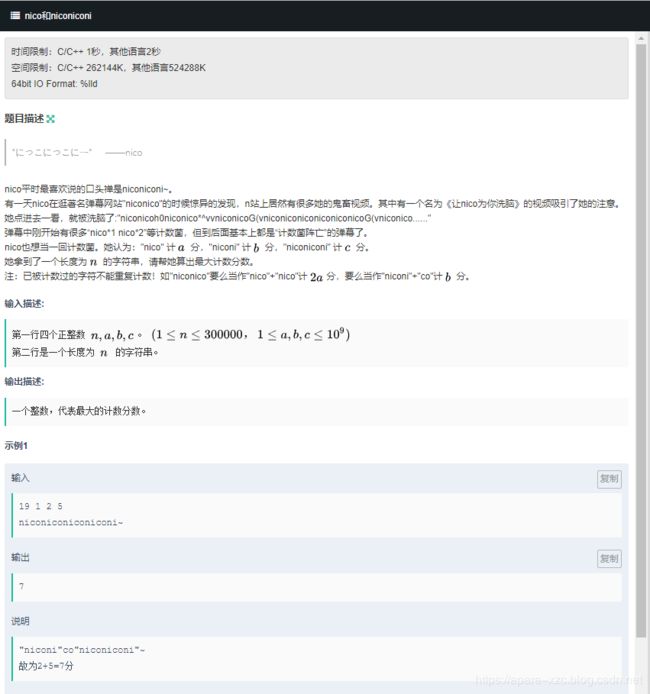
分析：
简单dp,官方题解说的很明白
我的代码：
#include J. u’s的影响力
题目链接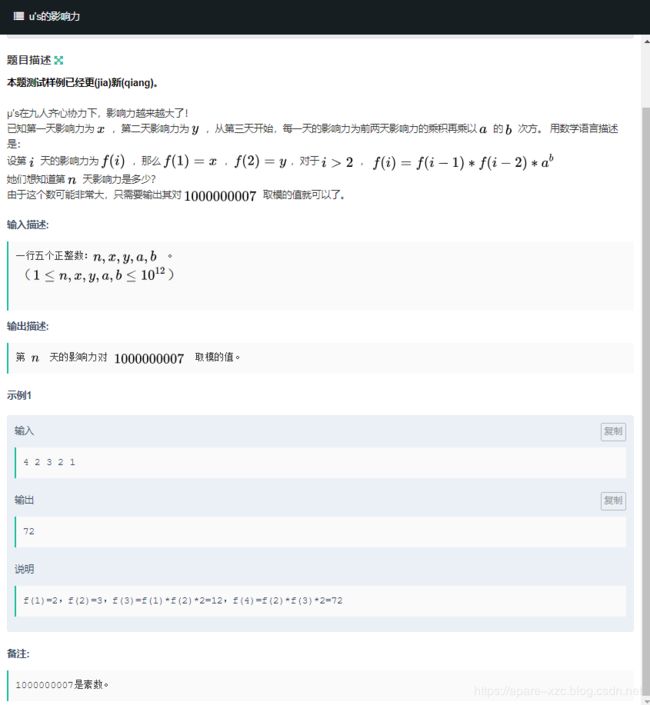
分析：
如果n<=2,直接输出x或y，如果n>=3,可以发现x和y的指数都是斐波那契数列的某一项，a^b的系数是也是某一项-1
Pab[i] = Pab[i-1] Pab[i-2] 1,一开始我直接退出一个三乘三的系数矩阵
// x[i 2] = x[i 1] x[i] 1
// |x[i 2]| |1 1 1| |x[i 1]| 0 x2 X[n 1]
// |x[i 1]| = |1 0 0| * |x[i 0]| 0 x1 -- n-1次 --> X[n]
// | 1 | |0 0 1| | 1 | 1
后来发现就是Feibonaci(n 1)-1
x的系数为Fei(n-1), y的系数为Fei(n) 如果像下面这样定义的话
// id 1 2 3 4 5 6 7 8 9
//Fei 0 1 1 2 3 5 8 13 21
//x 1 0 1 1 2 3 5 8 13 Fei(n-1)
//y 0 1 1 2 3 5 8 13 21 Fei(n )
//a^(b) 0 0 1 2 4 7 12 20 33 Fei(n 1)-1
我们可以用费马小定理，计算Fei[n]的时候用1000000007的欧拉函数作为模数。由于1E9 7是质数，质数的欧拉函数等于它自己减一，所以求Fei的时候对1E9 6取模即可。
由于x,y,a^b这三个底数可能是1E9 7的倍数，结果一定为0，要注意一下。
如果指数对1000000006取模后变为0，那么x^0 返回1，就会出错，所以建议快速幂这么写：
#define LL long long
LL fast_pow(LL a,LL b,LL mod)
{
if(a==0) return 0; //加一个特判以防万一
LL ans = 1;
while(b)
{
if(b&1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
求斐波那契额数列的第n项可以用矩阵快速幂，系数矩阵如下：
// fei[n ] = |1 1|^n-2 |fei[2]| 1
// fei[n-1] |0 1| * |fei[1]| 0
我的代码：
#include xzc
2020.2.6 1:08