数据结构与算法—最小生成树(Prim算法和Kruskal算法算法详解)
前言
在数据结构与算法的图论中,(生成)最小生成树算法是一种常用并且和生活贴切比较近的一种算法。但是可能很多人对概念不是很清楚。我们看下百度百科对于最小生成树定义:
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。 最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
通俗易懂的讲就是最小生成树包含原图的所有节点而只用最少的边和最小的权值距离。因为n个节点最少需要n-1个边联通,而距离就需要采取某种策略选择恰当的边。
从定义上分析,最小生成树其实是一种可以看作是树的结构。而最小生成树的结构来源于图(尤其是有环情况)。通过这个图我们使用某种算法形成最小生成树的算法就可以叫做最小生成树算法。具体实现上有两种实现方法、策略分别为kruskal算法和prim算法。
学习最小生成树实现算法之前我们要先高清最小生成树的结构和意义所在。咱么首先根据一些图更好的祝你理解。
一个故事
在中国城市道路规划中,是一门很需要科学的研究(只是假设学习不必当真)。城市道路铺设可能经历以下几个阶段。
- 初始,各个城市没有高速公路(铁路)。城市没有!
- 政府打算各个城市铺设公路(铁路),每个城市都想成为交通枢纽,快速到达其他城市!但是这种情况下国家集体资源跟不上、造价太昂贵。并且造成巨大浪费!
- 最终国家选择一些主要城市进行联通,有个别城市只能稍微绕道而行,而绕道太远的、人流量多的国家考虑新建公路(铁路)。适当提高效率。
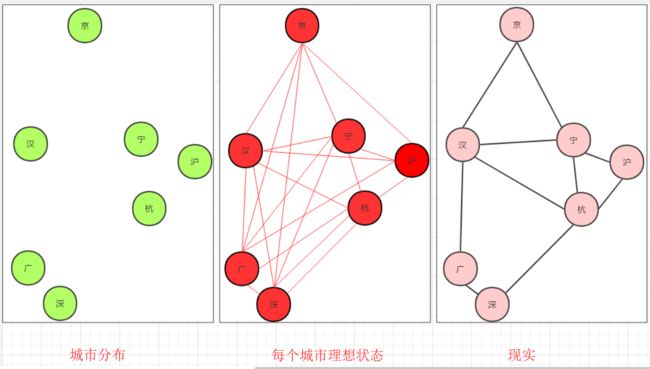
而随着国家科技互联网的进步,需要铺设高科技黄金外嵌光缆管道 (黄金夸张)联通整个国家使得信息能够快速传统、联通。(注意,咱们的通道是黄金的)对于有些可能重复的环。势必造成浪费。
所以我们要从有环图中选取代价和最小的路线一方面代价最小(总距离最小最省黄金)另一方面联通所有城市。
- 问题的
主要矛盾对问题起着决定性作用。主要矛盾次要矛盾相互影响,相互渗透,一定程度可以相互转化。故我们看问题要抓关键、找核心。 - 在公路时代城市联通的主要矛盾是时间慢,而造价相比运输时间是次要矛盾。所以在公路时代我们尽量使得城市能够直接联通,缩短城市联系时间。而稍微考虑建路成本!随着科技发展、信息传输相比公路运输很快,从而事件的主要矛盾从运输时间转变为造价成本。所以我们会关注联通所有点的路程(最短)。这就用到最小生成树算法。
而类似的还有局部区域岛屿联通修桥,海底通道这些高成本的都多多少少会运用。
Kruskal算法
上面介绍了最小生成树是什么,但是我们需要掌握和理解最小生成树如何形成。给你一个图,生成一个最小生成树,当然需要一定规则。而在实现最小生成树方面有prim和kruskal算法,这两种算法的策略有所区别,但是时间复杂度一致。
百度百科定义的基本思想:
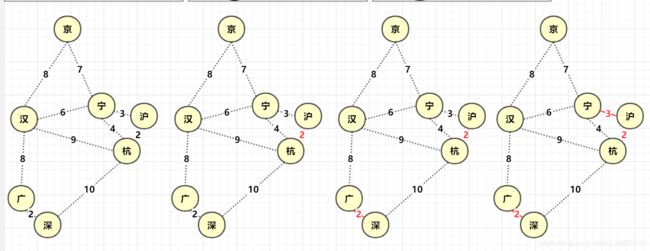
先构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直到森林中只有一棵树,也即子图中含有 n-1 条边为止。
简而言之,Kruskal算法进行调度的单位是边,它的信仰为:所有边能小则小,算法的实现方面和并查集(不相交集合)很像,要用到并查集判断两点是否在同一集合。
而算法的具体步骤为:
- 将边(以及2顶点)的对象依次加入集合(优先队列)
q1中。初始所有点相互独立。 - 取出当前
q1最小边,判断边的两点是否联通。 - 如果联通,跳过,如果不连通,则使用
union(并查集合并)将两个顶点合并。这条边被使用(可以储存或者计算数值)。 - 重复2,3操作直到集合(优先队列)
q1为空。此时被选择的边构成最小生成树。
Prim算法
除了Kruskal算法以外,普里姆算法(Prim算法)也是常用的最小生成树算法。虽然在效率上差不多。但是贪心的方式和Kruskal完全不同。prim算法的核心信仰是:从已知扩散寻找最小。它的实现方式和Dijkstra算法相似但稍微有所区别,Dijkstra是求单源最短路径。而每计算一个点需要对这个点从新更新距离。而prim甚至不用更新距离。直接找已知点的邻边最小加入即可!
对于具体算法具体步骤,大致为:
- 寻找图中任意点,以它为起点,它的所有边V加入集合(优先队列)
q1,设置一个boolean数组bool[]标记该位置已经确定。 - 从集合q1找到距离最小的那个边
v1并判断边另一点p是否被标记(访问),如果p被标记说明已经确定那么跳过,如果未被标(访问)记那么标记该点p,并且与p相连的未知点(未被标记)构成的边加入集合q1,边v1(可以进行计算距离之类,该边构成最小生成树) . - 重复1,2直到q1为空,构成最小生成树 !
大体步骤图解为:
因为prim从开始到结束一直是一个整体在扩散,所以不需要考虑两棵树合并的问题,在这一点实现上稍微方便了一点。
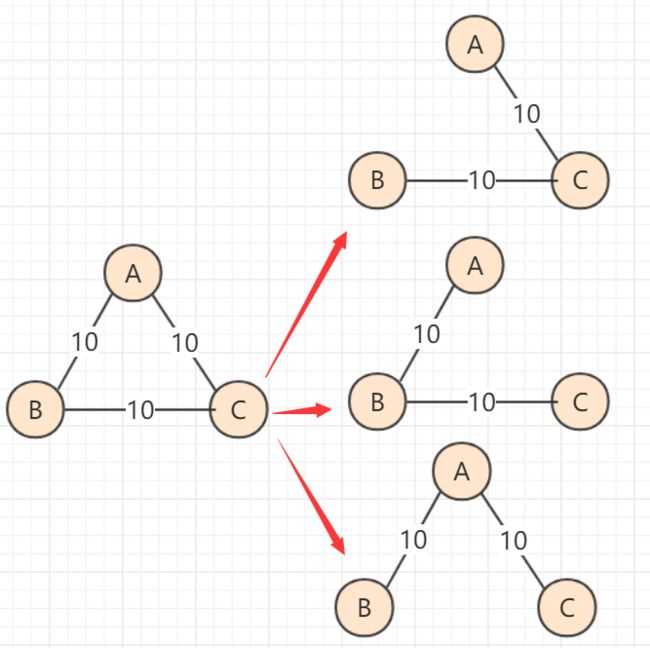
当然,要注意的是最小生成树并不唯一,甚至同一种算法生成的最小生成树都可能有所不同,但是相同的是无论生成怎样的最小生成树:
代码实现
上面分析了逻辑实现。下面我们用代码简单实现上述的算法。
prim
package 图论;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
public class prim {
public static void main(String[] args) {
int minlength=0;//最小生成树的最短路径长度
int max=66666;
String cityname[]= {"北京","武汉","南京","上海","杭州","广州","深圳"};
int city[][]= {
{ max, 8, 7, max, max, max, max }, //北京和武汉南京联通
{ 8, max,6, max,9, 8,max }, //武汉——北京、南京、杭州、广州
{ 7, 6, max, 3,4, max,max }, //南京——北京、武汉、上海、杭州
{ max, max,3, max,2, max,max }, //上海——南京、杭州
{ max, 9,4, 2,max, max,10 }, //杭州——武汉、南京、上海、深圳
{ max, 8,max, max,max, max,2 }, //广州——武汉、深圳
{ max, max,max, max,10,2,max }//深圳——杭州、广州
};// 地图
boolean istrue[]=new boolean[7];
//南京
Queue<side>q1=new PriorityQueue<side>(new Comparator<side>() {
public int compare(side o1, side o2) {
// TODO Auto-generated method stub
return o1.lenth-o2.lenth;
}
});
for(int i=0;i<7;i++)
{
if(city[2][i]!=max)
{
istrue[2]=true;
q1.add(new side(city[2][i], 2, i));
}
}
while(!q1.isEmpty())
{
side newside=q1.poll();//抛出
if(istrue[newside.point1]&&istrue[newside.point2])
{
continue;
}
else {
if(!istrue[newside.point1])
{
istrue[newside.point1]=true;
minlength+=city[newside.point1][newside.point2];
System.out.println(cityname[newside.point1]+" "+cityname[newside.point2]+" 联通");
for(int i=0;i<7;i++)
{
if(!istrue[i])
{
q1.add(new side(city[newside.point1][i],newside.point1,i));
}
}
}
else {
istrue[newside.point2]=true;
minlength+=city[newside.point1][newside.point2];
System.out.println(cityname[newside.point2]+" "+cityname[newside.point1]+" 联通");
for(int i=0;i<7;i++)
{
if(!istrue[i])
{
q1.add(new side(city[newside.point2][i],newside.point2,i));
}
}
}
}
}
System.out.println(minlength);
}
static class side//边
{
int lenth;
int point1;
int point2;
public side(int lenth,int p1,int p2) {
this.lenth=lenth;
this.point1=p1;
this.point2=p2;
}
}
}
Kruskal:
package 图论;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
import 图论.prim.side;
/*
* 作者:bigsai(公众号)
*/
public class kruskal {
static int tree[]=new int[10];//bing查集
public static void init() {
for(int i=0;i<10;i++)//初始
{
tree[i]=-1;
}
}
public static int search(int a)//返回头节点的数值
{
if(tree[a]>0)//说明是子节点
{
return tree[a]=search(tree[a]);//路径压缩
}
else
return a;
}
public static void union(int a,int b)//表示 a,b所在的树合并小树合并大树(不重要)
{
int a1=search(a);//a根
int b1=search(b);//b根
if(a1==b1) {//System.out.println(a+"和"+b+"已经在一棵树上");
}
else {
if(tree[a1]<tree[b1])//这个是负数,为了简单减少计算,不在调用value函数
{
tree[a1]+=tree[b1];//个数相加 注意是负数相加
tree[b1]=a1; //b树成为a的子树,直接指向a;
}
else
{
tree[b1]+=tree[a1];//个数相加 注意是负数相加
tree[a1]=b1; //b树成为a的子树,直接指向a;
}
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
init();
int minlength=0;//最小生成树的最短路径长度
int max=66666;
String cityname[]= {"北京","武汉","南京","上海","杭州","广州","深圳"};
boolean jud[][]=new boolean[7][7];//加入边需要防止重复 比如 ba和ab等价的
int city[][]= {
{ max, 8, 7, max, max, max, max },
{ 8, max,6, max,9, 8,max },
{ 7, 6, max, 3,4, max,max },
{ max, max,3, max,2, max,max },
{ max, 9,4, 2,max, max,10 },
{ max, 8,max, max,max, max,2 },
{ max, max,max, max,10,2,max }
};// 地图
boolean istrue[]=new boolean[7];
//南京
Queue<side>q1=new PriorityQueue<side>(new Comparator<side>() {//优先队列存边+
public int compare(side o1, side o2) {
// TODO Auto-generated method stub
return o1.lenth-o2.lenth;
}
});
for(int i=0;i<7;i++)
{
for(int j=0;j<7;j++)
{
if(!jud[i][j]&&city[i][j]!=max)//是否加入队列
{
jud[i][j]=true;jud[j][i]=true;
q1.add(new side(city[i][j], i, j));
}
}
}
while(!q1.isEmpty())//执行算法
{
side newside=q1.poll();
int p1=newside.point1;
int p2=newside.point2;
if(search(p1)!=search(p2))
{
union(p1, p2);
System.out.println(cityname[p1]+" "+cityname[p2]+" 联通");
minlength+=newside.lenth;
}
}
System.out.println(minlength);
}
static class side//边
{
int lenth;
int point1;
int point2;
public side(int lenth,int p1,int p2) {
this.lenth=lenth;
this.point1=p1;
this.point2=p2;
}
}
}
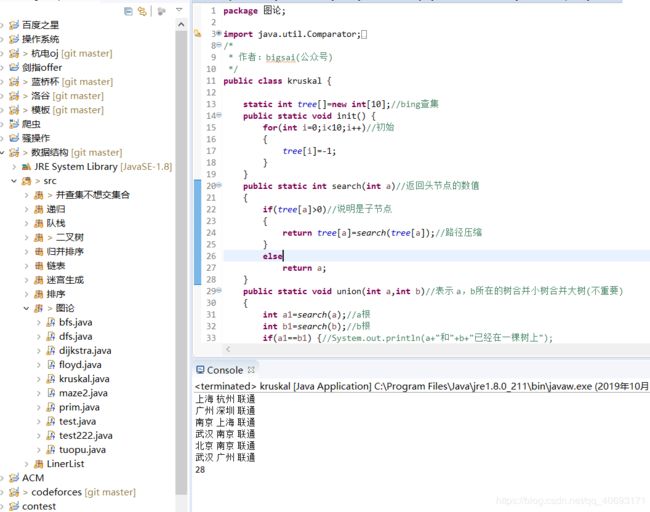
kruskal
总结
最小生成树算法理解起来也相对简单,实现起来也不是很难。Kruskal和Prim主要是贪心算法的两种角度。一个从整体开始找最小边,遇到关联不断合并,另一个从局部开始扩散找身边的最小不断扩散直到生成最小生成树。在学习最小生成树之前最好学习一下dijkstra算法和并查集,这样在实现起来能够快一点,清晰一点。
最后,如果你那天真的获得一大笔资金去修建这么一条昂贵的黄金路线,可以适当采取此方法,另外剩下的大批,,苟富贵,勿相忘。。
如果感觉还行,还请点个赞,关注一下吧,关注笔者公众号: bigsai回复数据结构即可获得数据结构的学习资料和视频一份!
![]()