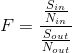通信系统指标解析

1 噪声

噪声通常是由器件和材料中的电荷或载流子的随机运行所产生的。根据产生机制的不同分为热噪声、散粒噪声、闪烁噪声、等离子噪声、量子噪声等。

1.1 噪声功率

                                                                                

式中

k-波尔兹曼常数 1. 380x10^-23 J/K;

T一热力学温度(K);

B-系统的带宽(Hz)。

在很多实际情况下，通常用等效噪声温度来表征噪声功率。

                                                                           

1.2噪声系数

噪声系数是对系统的输入和输出之间的信噪比递降的一种衡量度。

                                                                         

将噪声系数转化为等效噪声温度。

                                                                                 ---290K

 

在级联情况下，整个系统的噪声系数及等效噪声温度为:

                                                                   

                                                                  

2 灵敏度

在=290K的情况下，1Hz 带宽产生的噪声功率为:

     

            = -204dBW

            = -174dBm

而接收机的灵敏度计算为:

                                       S = -174dBm + NF + SNR + 10log(BW)

式中

NF-接收机噪声系数;

SNR -满足一定条件误码率所需的最低信噪比;

BW-接收机工作带宽。

3 线性度

系统的线性度一-般用1dB增益压缩点(PldB) 和三阶交截点(IP3) 来描述。

3.1 1dB增益压缩点（P1dB）

在实际系统中,输出响应严格正比于输人激励的理想化线性系统并不存在，一般的系统可以简单地描述成：

                                          

当输入信号为x(t) = Acos(wt)，系统的输出为：

                                 

因此，基频信号的系统增益为：

                               

对于大多数系统，a1和a3的符号相反，系统增益随着信号幅度A的增加而下降。如果用对数来表示系统的输人和输出信号幅度，可以清楚地看到输出功率随输人功率增大而偏离线性关系的情况。当输出功率与理想的线性情况偏离达到1dB时，系统的增益也下降了1dB，此时的输入信号功率值称为1dB增益压缩点(P1dB)如图所示。在PIdB点，信号幅度计算公式为：

     

                                            

                                                                         

                                                                        

                                                                       

3.2 三阶交截点（IP3）/ TOI

当系统输人两个频率靠得很近的信号时，在系统输出中除了会产生基波及其各次谐波外，还会产生频率之间的交调成分。假设输人信号为:

                                                                        

将信号代入：

                                                                      

得到系统的信号输出：

         

        

       从以上输出信号可以看出,在双音输人的情况下，系统输出产生了二阶、三阶及更高阶的产物，由于偶数阶交调产物离基频比较远，可以很方便地通过滤波器滤除，而奇数阶产物通常在滤波器通带内，很难滤除，尤其是以三阶产物幅度最大。因此，系统重点考虑的是三阶交调的影响。

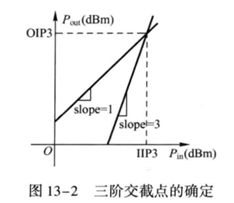
以dB为单位的坐标中，基频信号和三阶交调信号的斜率不同。因此，随着信号幅度A的增加，两条线必有一个交点，这个点就是三阶交截点(IP3)， 可以用输人功率表示(IIP3)或输出功率表示(OIP3)，如图所示。

在三阶交截点上，输人信号幅度的计算公式为：

                                                                                  

                                                                                

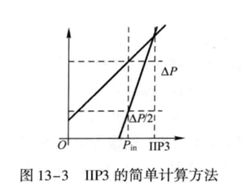
在实际系统中，可以根据下图所示计算方法推导出IIP3的简单计算公式为：

                                                                                 

上面的推导是基于两个输人信号的幅度相等的前提。在实际系统中，经常发生的一种情况是有用信号的幅度很小，而频率相差很近的干扰信号的幅度很大，这样会产生大信号阻塞。当输人信号为,其中，则系统输出信号为:

                                        

通常情况下，和符号相反，又因为，所以的值将变得很小，也就是基频的系统增益会急剧减小，即有用信号将被干扰信号阻塞了。

在级联情况下，整个系统的IP3计算公式为：

                                                           

对于复杂调制下的系统，除了上面的指标表现其线性度外，还有如邻道功率比( ACPR:信道带宽内信号功率和距中心频率△f处△B带宽内泄露或扩散的信号功率)和噪声功率比(NPR:测量非线性形成的带内干扰)等。

4 动态范围

受噪声和交调失真的影响，系统的工作范围限制在- -定范围内，输人功率的低端必须大于噪声电平，高端应该在交调失真限制极限以下。根据应用范围的不同，动态范围的定义也分为多种形式。

4.1 线性动态范围（LDR）

在噪声功率和1dB增益压缩点之间的范围定义为线性动态范围。
                                                                  

4.2 无寄生动态范围

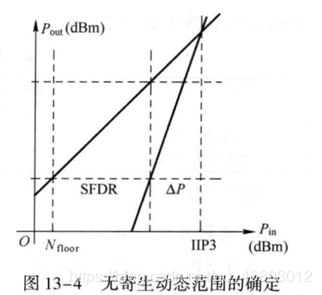
无寄生动态范围的定义为三阶交调功率与输出噪声相等时，输人信号与等效输人噪声之比，即在该范围内交调产物的功率值- -直小于噪声值，可以认为没有交调产物,交调产物也可以看作是寄生产物，这也是无寄生动态范围的物理意义。如图是无寄生动态范围的确定。

无寄生动态范围的确定，计算公式为：