2019中国大学生程序设计竞赛(CCPC) - 网络选拔赛 解题报告
1001 ^&^
Problem Description
Bit operation is a common computing method in computer science ,Now we have two positive integers A and B ,Please find a positive integer C that minimize the value of the formula (A xor C) & (B xor C) .Sometimes we can find a lot of C to do this ,So you need to find the smallest C that meets the criteria .
For example ,Let's say A is equal to 5 and B is equal to 3 ,we can choose C=1,3.... ,so the answer we're looking for C is equal to 1.
If the value of the expression is 0 when C=0, please print 1.
Input
The input file contains T test samples.(1<=T<=100)
The first line of input file is an integer T.
Then the T lines contains 2 positive integers, A and B, (1≤A,B<2^32)
Output
For each test case,you should output the answer and a line for each answer.
Sample Input
1
3 5Sample Output
1题意分析:
找出最小的值c使(a^c)&(b^c)最小。
#include
#include
using namespace std;
int main()
{
long long a, b, c;
int t;
scanf("%d", &t);
while(t--)
{
scanf("%lld%lld", &a, &b);
if((a&b)==0)
printf("1\n");
else
printf("%lld\n", a&b);
}
return 0;
} 1006 Shuffle Card(栈模拟)
Problem Description
A deck of card consists of n cards. Each card is different, numbered from 1 to n. At first, the cards were ordered from 1 to n. We complete the shuffle process in the following way, In each operation, we will draw a card and put it in the position of the first card, and repeat this operation for m times.
Please output the order of cards after m operations.
Input
The first line of input contains two positive integers n and m.(1<=n,m<=105)
The second line of the input file has n Numbers, a sequence of 1 through n.
Next there are m rows, each of which has a positive integer si, representing the card number extracted by the i-th operation.
Output
Please output the order of cards after m operations. (There should be one space after each number.)
Sample Input
5 3
1 2 3 4 5
3
4
3Sample Output
3 4 1 2 5题意分析:
最开始给出一个排列,然后m次操作,把a移动到最前面,求最后的排列
解题思路:
模拟栈,每次把给出的数放到栈顶,输出的时候记录一下如果已经输出过就不用再输出。比较坑的就是末尾不能输出换,否则PE。
#include
#include
#include
const int N = 1e5+10;
using namespace std;
bool book[N];
int a[N];
stacks;
int main()
{
int n, m, u;
while(scanf("%d%d", &n, &m)!=EOF)
{
for(int i=1; i<=n; i++)
scanf("%d", &a[i]);
for(int i=n; i>=1; i--)
s.push(a[i]);
while(m--)
{
scanf("%d", &u);
s.push(u);
}
memset(book, false, sizeof(book));
while(!s.empty())
{
u=s.top();
s.pop();
if(book[u]==false)
{
printf("%d ", u);
book[u]=true;
}
}
}
return 0;
} 1007 Windows Of CCPC(递归)
Problem Description
In recent years, CCPC has developed rapidly and gained a large number of competitors .One contestant designed a design called CCPC Windows .The 1-st order CCPC window is shown in the figure:
And the 2-nd order CCPC window is shown in the figure:
We can easily find that the window of CCPC of order k is generated by taking the window of CCPC of order k−1 as C of order k, and the result of inverting C/P in the window of CCPC of order k−1 as P of order k.
And now I have an order k ,please output k-order CCPC Windows , The CCPC window of order k is a 2k∗2k matrix.
Input
The input file contains T test samples.(1<=T<=10)
The first line of input file is an integer T.
Then the T lines contains a positive integers k , (1≤k≤10)
Output
For each test case,you should output the answer .
Sample Input
3
1
2
3Sample Output
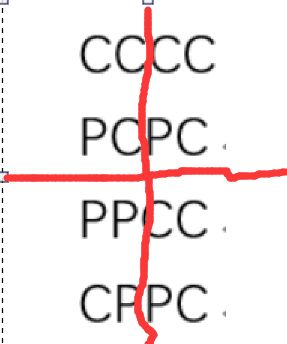
CC
PC
CCCC
PCPC
PPCC
CPPC
CCCCCCCC
PCPCPCPC
PPCCPPCC
CPPCCPPC
PPPPCCCC
CPCPPCPC
CCPPPPCC
PCCPCPPC题意分析:
用最初的可以拼成第2个,把第2个分成4部分,左下角和第一个相反,也就是P变为C,C变为P,其余相同。
解题思路:
一共要输出2^n行,那么可以一行一行的输出,假设我要输出总行为8行,现在要输出第1行,
那么其实是输出总行为4行的第1行输出两遍,
当输出左下角的部分时,这是总行为4行的相应行相反输出1遍,在输出1遍相同的。
#include
#include
void f(int n, int s, int t)
{
if(n==2)
{
if(t==1) {
if(s==1)
printf("CC");
else printf("PC");
}
else {
if(s==1)
printf("PP");
else printf("CP");
}
return ;
}
int x=s%(n/2);
if(x==0)
x=n/2;
if(t==1)
{
if(s>n*1.0/2)
f(n/2, x, 0);
else f(n/2, x, 1);
f(n/2, x, 1);
}
else if(t==0){
if(s>n*1.0/2)
f(n/2, x, 1);
else f(n/2, x, 0);
f(n/2, x, 0);
}
}
int main()
{
int t, n;
scanf("%d", &t);
while(t--)
{
scanf("%d", &n);
n=pow(2, n);
for(int i=1; i<=n; i++) {
f(n, i, 1);
printf("\n");
}
}
return 0;
}
1008 Fishing Master(优先队列+贪心)
Problem Description
Heard that eom is a fishing MASTER, you want to acknowledge him as your mentor. As everybody knows, if you want to be a MASTER's apprentice, you should pass the trial. So when you find fishing MASTER eom, the trial is as follow:
There are n fish in the pool. For the i - th fish, it takes at least ti minutes to stew(overcook is acceptable). To simplify this problem, the time spent catching a fish is k minutes. You can catch fish one at a time and because there is only one pot, only one fish can be stewed in the pot at a time. While you are catching a fish, you can not put a raw fish you have caught into the pot, that means if you begin to catch a fish, you can't stop until after k minutes; when you are not catching fish, you can take a cooked fish (stewed for no less than ti) out of the pot or put a raw fish into the pot, these two operations take no time. Note that if the fish stewed in the pot is not stewed for enough time, you cannot take it out, but you can go to catch another fish or just wait for a while doing nothing until it is sufficiently stewed.
Now eom wants you to catch and stew all the fish as soon as possible (you definitely know that a fish can be eaten only after sufficiently stewed), so that he can have a satisfying meal. If you can complete that in the shortest possible time, eom will accept you as his apprentice and say "I am done! I am full!". If you can't, eom will not accept you and say "You are done! You are fool!".
So what's the shortest time to pass the trial if you arrange the time optimally?
Input
The first line of input consists of a single integer T(1≤T≤20), denoting the number of test cases.
For each test case, the first line contains two integers n(1≤n≤10^5),k(1≤k≤10^9), denoting the number of fish in the pool and the time needed to catch a fish.
the second line contains n integers, t1,t2,…,tn(1≤ti≤10^9) ,denoting the least time needed to cook the i - th fish.
Output
For each test case, print a single integer in one line, denoting the shortest time to pass the trial.
Sample Input
2
3 5
5 5 8
2 4
3 3Sample Output
23
11Hint
Case 1: Catch the 3rd fish (5 mins), put the 3rd fish in, catch the 1st fish (5 mins), wait (3 mins), take the 3rd fish out, put the 1st fish in, catch the 2nd fish(5 mins), take the 1st fish out, put the 2nd fish in, wait (5 mins), take the 2nd fish out. Case 2: Catch the 1st fish (4 mins), put the 1st fish in, catch the 2nd fish (4 mins), take the 1st fish out, put the 2nd fish in, wait (3 mins), take the 2nd fish out.
题意分析:
有n条鱼,每条鱼要煮相应的时间才能吃,捕一条鱼的时间是相同的,在捕鱼的时间内不能做其他事,可以捕多条鱼,求把所有的鱼都煮熟需要多少时间。
解题思路:
抓第一条鱼的耗时是无法避免的,抓鱼应该从烹饪时间最长的开始抓起,这样才可以用烹饪时间去抓更多的鱼,而剩下的不够抓一条鱼的烹饪时间应该存下来,后面在抓鱼的时候从这些时间中选出最大的x,抓鱼的时间会和烹饪的时间重合最多,这样可以使时间(k-x)最小。
#include
#include
#include
const int N = 1e5+10;
using namespace std;
long long a[N];
int cmp(long long a, long long b)
{
return bq;
scanf("%d", &t);
long long sum;
while(t--) {
while(!q.empty())
q.pop();
scanf("%d%lld", &n, &k);
for(i=0; i0) {
t--;
sum+=a[i];
t+=a[i]/k;
if(a[i]%k)
q.push(a[i]%k);
}
else {
break;
}
}
for(; i