线性回归(Linear Regression)
线性回归(Linear Regression)
- 前置知识
- 回归平均
- 拟合
- 损失函数
- 算法原理
- 数学推导(可跳过)
- 算法实现
- 向量化
- s c i k i t − l e a r n scikit-learn scikit−learn调包实现
- 线性回归衡量指标
- MSE
- RMSE
- MAE
- R Squared
- 多元线性回归
- 线性回归总结
前置知识
前置知识:回归效应、拟合、损失函数。
回归平均
1877年,高尔顿(达尔文的表弟)在英国皇家科学院做了一个演示报告:回归平均。
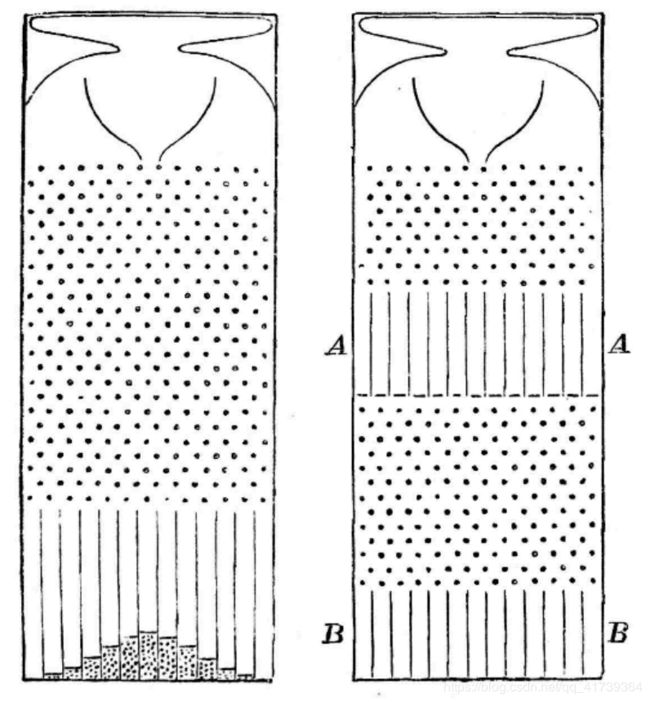
高尔顿这次演示的东西,被后世称为“高尔顿板”。

它是一个平板,下部有很多垂直的槽,槽上面是一些排列成三角形的小格挡。
让一个小球从最上方掉下去,它会经过各个隔挡的阻碍,最终落到一个竖槽里。每个小球在进入竖槽之前的运动都是随机的,但是当你放了很多很多小球之后,它们就会在竖槽上呈现一个明显有规律的分布:一条钟形曲线。
这就是正态分布。高尔顿板演示的是人的遗传。比如身高和智商,可能受多个遗传因素的影响 —— 就好像高尔顿板上的那些隔挡 —— 这些因素综合起来一起作用,结果就一定是正态分布。
事实上人的身高和智商的确就是正态分布。可以想象上面图中横坐标代表身高,纵坐标代表每个身高值上的人数,正态分布是说,身高特别高和特别矮的人都很少。
高尔顿说如果我在竖槽下面再放上一些隔挡,然后隔挡下面再放上第二排竖槽,就如同下图中右边那样,会是什么样的情景?
这就模拟了两代人的身高。第一排,也就是竖槽 A A A,代表第一代人的身高分布,我们知道是正态分布。那么第一代人再遗传一次,到达竖槽 B B B,会是什么分布?
是更加宽广的正太分布,可真实世界的变换并没有这样。
现实里,有一批身高特别高的人,如果他们生的孩子是在他们的身高基础上进一步随机演化的话,其中应该有一半人的身高比父辈高。
但是这并没有发生,真实世界里牛人的第二代并没有一半的机会比牛人强。
那个时候,人们都只知道:因果关系,并没有什么相关性。
高尔顿也深陷因果思维,所以思考 父代与子代之间的关系 时一直想了 12 12 12 个年头。
他考察英国男子的身高和手臂之间的关系,发现身高特别高的人,手臂也都很长 —— 但是他们的手臂并不是最长的。
这就好像最聪明的父亲没有生出最聪明的儿子一样。手臂相对于身高,也出现了回归平庸。
父亲跟儿子之间也许有因果关系,身高跟手臂之间似乎不太可能有因果关系啊。
更进一步,父亲相对于儿子,也有一个回归平均!
如果先看儿子身高,那些最高的儿子,他们的父亲的身高也不是最高的。显然儿子身高并不能决定父亲的身高,这个关系肯定不是因果关系!
高尔顿把这种关系叫“相关”。这就是“相关性”这个概念的起源。高尔顿是第一个意识到“相关不是因果”的人。
儿子出生的时候父亲已经成年了,儿子身高总不可能影响父亲的身高,所以绝对不可能有一种什么神秘力量,决定了从儿子到父亲的回归平均。
具体到身高来说,我们的身高有一部分是直接继承了父母的基因,还有一部分是遗传基因的排列组合、跟环境的相互作用影响到基因表达,这些过程中发生的一些运气。
高个父亲不但有好基因,而且有好运气。基因可以遗传,可是运气不能遗传。好运气总是非常罕见的,所以大概率下,儿子不会有那么好的运气 —— 所以儿子的身高就不如父亲。
这种回归效应,是大自然将人类身高的分布约束在相对稳定而不产生俩极分化的整体水平,数据向平均值靠拢…。生活里,有很多事情都有回归效应的:
- 从长期来讲,股票的价格会回归其价值。
高尔顿不得不把高尔顿板做了一个改进,把一些竖槽变成斜槽,才能体现这个回归效应:

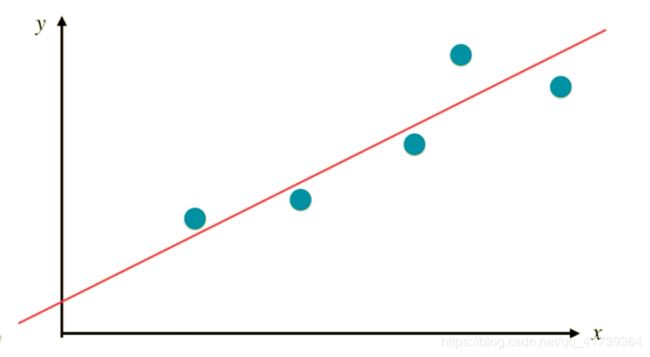
在分析了 1078 1078 1078 对父子的身高之后,发现这些数据的散点图大致呈直线状态,就可以把这俩个变量之间具有的线性相关的关系,这条直线称为回归直线(regression line)。
如果能够求出这条回归直线方程,就可以清楚的了解 变量 x x x 与 变量 y y y 之间的相关性,如同平均数可以作为一个变量的数据的代表一样,这条直线也可以作为俩个变量具有线性相关关系的代表。
高尔顿推导出了一个线性回归的表达式: y = 0.516 x + 33.73 y=0.516x+33.73 y=0.516x+33.73。
- x x x:父代身高
- y y y:子代身高
后来,人们把由一个变量的变化去推测另一个变量的变化的方法,称为“线性回归”。
线性回归是假设数据有线性相关的关系,要找到一条直线,最好的拟合所有的样本点。
拟合
-
什么叫拟合?
在散点图上,画直线发现趋势的这个动作,就叫“拟合”。
-
什么叫过拟合?
画的线(实际上是曲线)经过散点图上的每一个点,就是“过拟合”。
一丝不苟地反映已知的所有数据,那对未知数据的预测能力就会非常差。
这是因为所谓的“已知”数据,都是有误差的!精准的拟合会把数据的误差给放大 ——拟合得越精确,并不代表预测结果就越准确,拟合得过度精确后反而结果更加糟糕。
-
什么叫最好的拟合?
如果用数学语言表达:损失函数最小。
损失函数的公式把这两个点相减平方求和以后得到的是,每个真实值与预测值差距的平方和,这个值衡量了我们的预测值和真实值之间的差距,越小越好。
损失函数
-
什么叫损失函数?
损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。不同的模型用的损失函数一般也不一样,所以损失函数有好多好多种。
我们现在对这个问题只是求一下最小平方损失,这是我们的损失函数。我们为什么不用 3 、 4 3、4 3、4 次方,不用绝对值做损失呢。因为这个平方损失是我们假设 y y y 的观测值存在一个正态分布的误差,我们最大似然 y y y 的概率来的,在概率上有实际意义的支持。
似然估计就不介绍了,因为学习机器学习时更应关心的特定问题下,人们是如何设计损失函数的… …还有名词太多,把小白绕晕了咋办!
算法原理
假定,我们预测房屋价格是线性关系,变量 x x x 是 房屋面积,变量 y y y 是 房屋价格。
我们收集了一组数据:
| x | y |
|---|---|
| 3.60 | 1.00 |
| 3.70 | 0.90 |
| 3.80 | 0.90 |
| 3.90 | 0.81 |
| 4.00 | 0.60 |
| 4.10 | 0.56 |
| 4.20 | 0.35 |
P.S. 数据并不真实,关注思想即可,别太关注数据的细节,小心过度拟合!

将散点图上的数据连起来的趋势,接近一条直线,故用 y = a x + b y=ax+b y=ax+b 表示,可以将上面的数值代入表达式:
- 3.6 a + b − 1.00 = 0 3.6a+b-1.00=0 3.6a+b−1.00=0
- 3.7 a + b − 0.90 = 0 3.7a+b-0.90=0 3.7a+b−0.90=0
- 3.8 a + b − 0.90 = 0 3.8a+b-0.90=0 3.8a+b−0.90=0
- 3.9 a + b − 0.81 = 0 3.9a+b-0.81=0 3.9a+b−0.81=0
- 4.0 a + b − 0.60 = 0 4.0a+b-0.60=0 4.0a+b−0.60=0
- 4.1 a + b − 0.56 = 0 4.1a+b-0.56=0 4.1a+b−0.56=0
- 4.2 a + b − 0.35 = 0 4.2a+b-0.35=0 4.2a+b−0.35=0
由于直线只有俩个未知数 a , b a, ~b a, b,理论上只需要俩个方程就能得解… …但实际不可能,因为所有点并没有真正的位于同一条直线上,因此不可能所有的数值都满足:
- a x + b − y = 0 ax+b-y=0 ax+b−y=0
所以,我们不需要真实的 a , b a,~b a, b,只需要找到一对合理的 a , b a,~b a, b,误差最小即可。
而后,我们就会使用损失函数。
- 损失函数: ∑ ( y i − a x i − b ) 2 = ( y 0 − a x 0 − b ) 2 + ( y 1 − a x 1 − b ) 2 + . . . + ( y n − a x n − b ) 2 \sum(y_{i}-ax_{i}-b)^{2}=(y_{0}-ax_{0}-b)^{2}+(y_{1}-ax_{1}-b)^{2}+...+(y_{n}-ax_{n}-b)^{2} ∑(yi−axi−b)2=(y0−ax0−b)2+(y1−ax1−b)2+...+(yn−axn−b)2
损失函数里的 − ( a x i + b ) -(ax_{i}+b) −(axi+b) 是预测的合理的值 y i ′ y_{i}' yi′,损失函数里的 y i y_{i} yi 才是真实的值。
那损失函数就是使 ( 真 值 − 预 测 的 值 ) 2 (真值 - 预测的值)^{2} (真值−预测的值)2 最小(没拟合的部分最少),误差的平方也叫二乘方,故名“最小二乘法”,二乘即误差,代表最小化误差的平方。
几乎所有参数学习算法都是这样的套路:
- 通过分析问题,确定问题的损失函数,接着最优化损失函数,获得机器学习的模型。
- 有线性回归、多项式回归、逻辑回归、SVM、神经网络等等。
通过最小二乘法,求解出 a , b a,~b a, b 都有直接的数学表达式:

- x ˉ , y ˉ \bar{x}, \bar{y} xˉ,yˉ 是均值
具体的推导,看不看随意,因为知道最后的数学表达式就可以写程序了。
数学推导(可跳过)
算法实现
先把数据部分准备好:
import numpy as np
import matplotlib.pyplot as plt
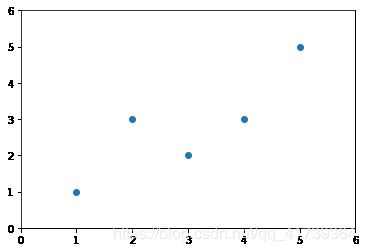
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])
plt.scatter(x, y)
plt.axis([0, 6, 0, 6])
plt.show()
# 获取平均值
x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0
d = 0.0
# 模拟a
for x_i, y_i in zip(x, y):
num += (x_i - x_mean) * (y_i - y_mean)
d += (x_i - x_mean) ** 2
a = num/d
# 模拟b
b = y_mean - a * x_mean
# 绘制直线
y_hat = a * x + b
# 可视化
plt.scatter(x, y)
plt.plot(x, y_hat, color='r')
plt.axis([0, 6, 0, 6])
plt.show()
# 新x
x_predict = 6
# 预测y
y_predict = a * x_predict + b
print(y_predict) # 输出:5.2000000000000002
封装为一个类,完整代码:
import numpy as np
class LinearRegression:
def __init__(self):
"""初始化 Linear Regression 模型"""
self.a_ = None
self.b_ = None
def fit(self, x_train, y_train):
"""根据训练 数据集x_train, y_train 训练 Linear Regression 模型"""
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
num = 0.0
d = 0.0
for x, y in zip(x_train, y_train):
num += (x - x_mean) * (y - y_mean)
d += (x - x_mean) ** 2
self.a_ = num / d
self.b_ = y_mean - self.a_ * x_mean
return self
def predict(self, x_predict):
"""给定待预测 数据集x_predict,返回表示 x_predict 的结果向量"""
return np.array([self._predict(x) for x in x_predict])
def _predict(self, x_single):
"""给定单个待预测 变量x,返回 x 的预测结果值"""
return self.a_ * x_single + self.b_
def __repr__(self):
return "LinearRegression()"
向量化
s c i k i t − l e a r n scikit-learn scikit−learn调包实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LinearRegression # 线性回归在 linear_model
from sklearn.model_selection import train_test_split
# 从 sklearn 的 datasets 中导入波士顿房价数据集
boston = datasets.load_boston()
X_data = boston.data
y_data = boston.target
# 划分数据集,一部分用于训练,另一部分用来做测试,sklearn中自然也有相应的方法可以直接实现,其中random_state是一个随机种子,可以是任意一个数
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size = 0.3, random_state = 42)
model = LinearRegression()
model.fit(X_train, y_train)
# 已经训练好了一个线性回归模型,调用model.predict可以预测某一个或者某一些输入值相应的输出
print( model.score(X_test, y_test )
线性回归衡量指标
MSE
RMSE
MAE
R Squared
多元线性回归
线性回归总结
线性回归的可解释性好,所以是一个可以学习到知识的算法。
线性回归用于预测线性关系越强的数据,线性回归的效果就越好。
量化交易的回报一般取决于两个因素:
- 数学模型的好坏;
- 是否能找到别人不知道的信号。
为了让自己的数学模型比竞争对手好,对冲基金从来是最先尝试新技术的一族,我们今天说的各种机器学习的算法, 20 20 20 年前对冲基金早就尝试使用了。
今天很多人学了点机器学习的方法,就试图自己用模型炒股,那是过高估计自己的能力了,这些人在用真金白银炒股时,应该先了解一下这个行业的现状。
不要学了一些机器学习的算法,就兴冲冲的梦想发大财。
现在人工智能算法这么牛,华尔街里面高盛的很多交易员都被解雇了,那是不是将来 AI 就会控制我们的整个投资行业?
至少在现在这个阶段,AI 的算法我觉得是不能够取代人类的,当然存在个别 AI 算法能够比我们的投资策略好,这都是特例,没有什么普遍性的意义。
为什么 AI 现在不一定能行呢?
一个最重要的原因是因为,如果用人工智能,它很容易过度拟合。
一般用这些 AI 算法是怎么做的呢?
先找一堆数据,很多数据有很多变量,用这些变量去预测股票将来的收益率,都是先在一个样本里面去做。
因为数据量特别多,这些算法也比较复杂,容易过度拟合,这是什么意思呢?
是指找到统计上的一些假象,这个训练本来 X X X和 Y Y Y的收益率是没有关系的,只不过是碰运气碰上关系了,但却用这个东西去做策略,真的在实操的时候可能这个变量就没有用了。
因为过度拟合这个问题,所以说 机器学习 不一定能战胜人类。
但是这当然不意味着 机器学习 是没有用的,至少用的是比较高级的回归分析方法,它肯定比正常的线性回归会有用,只要用得好。比如说:
- 有 100 100 100个信号,每个信号的频率是不一样的,那怎么把这 100 100 100 个信号组合起来?
其实这个时候一些算法比我们平时用标准的线性回归方法可以组合得更好,它确实会有用,只不过没有想象中的那么有用。比如说:
- 那 100 100 100 个信号还是先从最基础的心理学、经济学原理选出来的,选出来之后再用这些算法去做可能会更好一点,但是你直接让 AI 去选信号,是容易产生过度拟合的问题。
所以,千万不要认为一些基金的名字里面加个“AI”、加个“人工智能”,你就觉得它特别牛,你就去买这个基金… …还不如买指数妥妥的。