机器学习系列笔记十三: 集成学习/模型聚合
机器学习系列笔记十三: 集成学习/模型聚合
文章目录
- 机器学习系列笔记十三: 集成学习/模型聚合
- 什么是集成学习
- Voting
- Hard Voting
- 模拟实现Hard Voting 集成学习
- 使用Voting Classifier
- Soft Voting
- 使用Soft Voting实现集成学习
- Bagging
- 对Bagging的使用
- OOB与关于Bagging的更多讨论
- 随机森林与Extra-Trees
- 随机森林
- 使用随机森林
- Extra-Trees
- 使用Extra-Trees
- 集成学习解决回归问题
- Boosting
- AdaBoost
- 使用Ada Boosting
- Gradient Boosting
- 使用Gradient Boosting
- Stacking
- Stacking的使用
- 总结
- 参考致谢
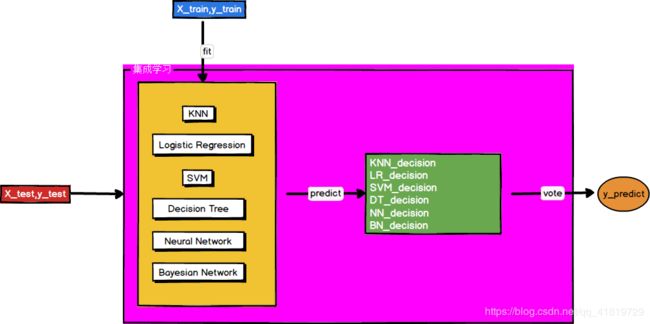
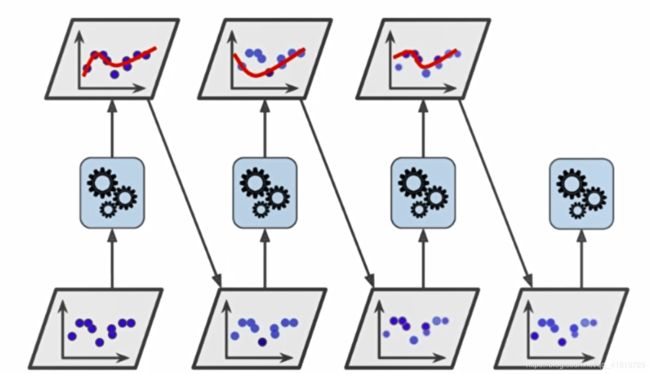
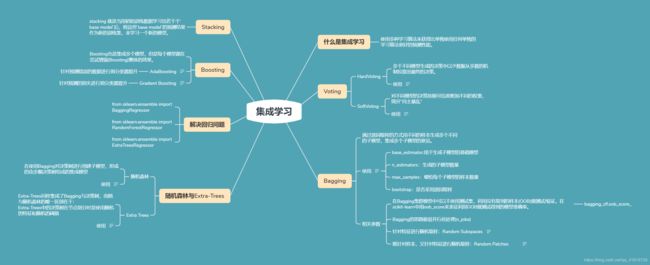
什么是集成学习
维基百科定义
在统计学和机器学习中,集成学习方法使用多种学习算法来获得比单独使用任何单独的学习算法更好的预测性能。
评估集成学习的预测通常需要比评估单个模型的预测更多的计算,因此集成可以被认为是通过执行大量额外计算来补偿差的学习算法的方式。诸如决策树之类的快速算法通常用于**方法(如随机森林),尽管较慢的算法也可以从集成方法中受益。
通过类比,集成技术也已用于无监督学习场景中,如共识聚类或异常检测。
集成学习本身是一种监督学习算法,因为它可以被训练然后用于进行预测。因此,训练后的集成模型代表了一个假设,但这个假设不一定被包含在构建它的模型的假设空间内。因此,可以证明集成学习在它们可以表示的功能方面具有更大的灵活性。理论上,这种灵活性使他们能够比单一模型更多地过拟合训练数据,但在实践中,一些集成算法(如Bagging算法)倾向于减少对训练数据过拟合相关的问题。
Voting
生活中的Voting集成学习
- 从豆瓣评分中寻找好看的电影
- 从购买评价中决定是否购买该物品
- 疑难病情专家会诊
通过Voting方式的集成学习,我们可以从多个决策中以少数服从多数的机制投票出最终的决策。
在scikit-learn中给我们提供了Voting Classfier接口来实现集成学习。
Hard Voting
模拟实现Hard Voting 集成学习
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
from sklearn import datasets
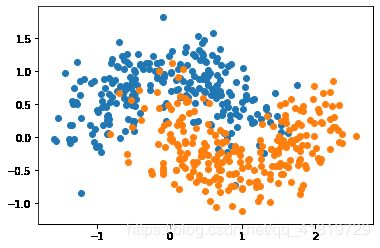
X,y = datasets.make_moons(n_samples=500,noise=0.3,random_state=42)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
切割数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42)
首先看看逻辑回归模型的效果
from sklearn.linear_model import LogisticRegression
log_clf = LogisticRegression()
log_clf.fit(X_train,y_train)
log_clf.score(X_test,y_test)
0.864
看看SVM模型的效果
from sklearn.svm import SVC
svm_clf = SVC()
svm_clf.fit(X_train,y_train)
svm_clf.score(X_test,y_test)
0.888
看看决策树模型的效果
from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier()
dt_clf.fit(X_train,y_train)
dt_clf.score(X_test,y_test)
0.84
得到上面三个模型对同一个测试集的预测结果
y_predict1 = log_clf.predict(X_test)
y_predict2 = svm_clf.predict(X_test)
y_predict3 = dt_clf.predict(X_test)
通过少数服从多数的原则,投票出最终的预测结果
y_predict = np.array((y_predict1+y_predict2+y_predict3)>=2,dtype=int)
y_predict[:10]
array([1, 0, 0, 1, 1, 1, 0, 0, 0, 0])
看看这个预测结果的准确率如何
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_predict)
0.896
可以看到相比前面三个模型单独预测,集成后提高了预测结果的准确度
使用Voting Classifier
from sklearn.ensemble import VotingClassifier
voting_clf = VotingClassifier(estimators=[
('log_clf',LogisticRegression()),
('svm_clf',SVC()),
('dt_clf',DecisionTreeClassifier())
],voting="hard")
通过管道的方式给estimators赋值(各种模型),这里voting="hard"表示采用少数服从多数的机制得到最终决策
voting_clf.fit(X_train,y_train)
voting_clf.score(X_test,y_test)
0.904
Soft Voting
在前面对Voting Classifier的使用中,传入了voting="hard",采用少数服从多数(一人一票)的机制得到最终决策。
而这样的选举机制其实是不合理的,如果有了解过社会学的同志们都知道一个词叫民主暴政,当年苏格拉底好像就是被希腊的公民门一人一票给投死的。所以,为避免这种情况的发生,就不应该采用一人一票的投票机制,换言之,应该在投票的基础上为各个选票赋予权重,对于更精英、更专业的人士的投票应该加重权值,对更normal,更普通的边缘人士的投票应该减少权值。
这样的选举(投票)机制就称之为Soft Voting

对Soft Voting的实现要求参与集成学习各个模型都能估计预测结果的概率判定门限。
-
逻辑回归本身就是基于概率模型的
-
KNN 算法也可支持计算概率(decision_neighbors/n_neighbors)
-
决策树算法支持计算概率(占比例最大的数据点数量/叶子节点中所有的数据点的数量)
-
SVM 算法可以通过一些改进手段使得其支持计算概率
-
probability: bool, default=False
Whether to enable probability estimates. This must be enabled prior to calling
fit, will slow down that method as it internally uses 5-fold cross-validation, andpredict_probamay be inconsistent withpredict. Read more in the User Guide.
-
使用Soft Voting实现集成学习
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
from sklearn import datasets
from sklearn.model_selection import train_test_split
X,y = datasets.make_moons(n_samples=500,noise=0.3,random_state=42)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
Hard Voting Classifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import VotingClassifier
voting_clf = VotingClassifier(estimators=[
('log_reg',LogisticRegression()),
('svm_clf',SVC()),
('dt_clf',DecisionTreeClassifier(random_state=666))
],voting="hard")
voting_clf.fit(X_train,y_train)
voting_clf.score(X_test,y_test)
0.896
Soft Voting Classifier
voting_clf2 = VotingClassifier(estimators=[
('log_reg',LogisticRegression()),
('svm_clf',SVC(probability=True)),
('dt_clf',DecisionTreeClassifier(random_state=666))
],voting="soft")
voting_clf2.fit(X_train,y_train)
voting_clf2.score(X_test,y_test)
0.912
可以看到在大多数情况下Soft Voting Classifier的效果是要比Hard Voting Classifier好的
Bagging
采用上面描述的方式进行集成学习存在一个问题:
- 虽然有很多机器学习方法,但是从投票的角度来看,仍然不够多
解决方案:
- 创建更多的子模型,集成更多子模型的意见。
- 子模型之间不能一致,子模型之间要有差异性。
如何创建差异性:
-
每个子模型只看样本数据的一部分。
例如:一共500个样本,每个子模型只看哈希生成的100个样本数据 -
每个子模型不需要太高的准确率
例如:如果每个子模型只有51%的准确率,-
此时如果只有一个子模型,整体准确率为51%,
-
如果我们有3个子模型,整体准确率为 0.5 1 3 + C 1 3 ∗ 0.5 1 2 ∗ 0.49 = 51.5 % 0.51^3+C_1^3*0.51^2*0.49=51.5\% 0.513+C13∗0.512∗0.49=51.5%
-
如果我们有500个子模型,整体准确率为 ∑ i = 251 500 C 500 i ⋅ 0.5 1 i ⋅ 0.4 9 500 − i = 65.6 % \sum^{500}_{i=251}C_{500}^i \cdot 0.51^i\cdot0.49^{500-i}=65.6\% ∑i=251500C500i⋅0.51i⋅0.49500−i=65.6%
-
在创建差异性,使得每个子模型只看样本数据的一部分时,通常由两种方案:
- 放回取样:Bagging(更常用)
- 在统计学中的放回取样:bootstrap
- 不放回取样:Pasting
Bootstrap聚合(Bootstrap Aggregating,Bagging)使集成模型中的每个模型在投票时具有相同的权重。为了减小模型方差,Baging使用随机抽取的子训练集训练集成中的每个模型。例如,随机森林算法将随机决策树与Bagging相结合,以实现更高的分类准确度。
对Bagging的使用
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
from sklearn import datasets
from sklearn.model_selection import train_test_split
X,y = datasets.make_moons(n_samples=500,noise=0.3,random_state=42)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
使用Bagging
class sklearn.ensemble.BaggingClassifier(base_estimator=None, n_estimators=10, *, max_samples=1.0, max_features=1.0, bootstrap=True, bootstrap_features=False, oob_score=False, warm_start=False, n_jobs=None, random_state=None, verbose=0)
BaggingClassifier的参数含义:
- base_estimator:用于生成子模型的基础模型
- n_estimators:生成的子模型数量
- max_samples:喂给每个子模型的样本数量
- bootstrap:是否采用放回取样
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),n_estimators=10,max_samples=100,bootstrap=True)
bagging_clf.fit(X_train,y_train)
bagging_clf.score(X_test,y_test)
0.88
生成100个子模型
bagging_clf2 = BaggingClassifier(DecisionTreeClassifier(),n_estimators=100,max_samples=100,bootstrap=True)
bagging_clf2.fit(X_train,y_train)
bagging_clf2.score(X_test,y_test)
0.912
OOB与关于Bagging的更多讨论
OOB :Out-Of-Bag,放回取样导致一部分样本很有可能没有取到,平均大约有37%的样本没有取到,而这些没有被取到的样本就称之为OOB。
所以可以不使用测试集,利用这部分没有取到的样本(OOB)做测试/验证。在scikit-learn中用oob_score来表征利用OOB做测试得到的模型准确率。
oob_score_
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
n_estimators=500,
max_samples=100,
bootstrap=True,
oob_score=True)
bagging_clf.fit(X,y)
BaggingClassifier(base_estimator=DecisionTreeClassifier(class_weight=None,
criterion='gini',
max_depth=None,
max_features=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
presort=False,
random_state=None,
splitter='best'),
bootstrap=True, bootstrap_features=False, max_features=1.0,
max_samples=100, n_estimators=500, n_jobs=None,
oob_score=True, random_state=None, verbose=0,
warm_start=False)
bagging_clf.oob_score_
0.92
Bagging的思路极易并行化处理(n_jobs)
%%time
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
n_estimators=5000,
max_samples=100,
bootstrap=True,
oob_score=True)
bagging_clf.fit(X,y)
Wall time: 3.45 s
%%time
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
n_estimators=5000,
max_samples=100,
bootstrap=True,
oob_score=True,
n_jobs=-1)
bagging_clf.fit(X,y)
Wall time: 1.86 s
bootstrap_features
针对特征进行随机取样:Random Subspaces
random_subspaces_clf = BaggingClassifier(DecisionTreeClassifier(),
n_estimators=500,
max_samples=500, # 数据集样本为500
bootstrap=True,
oob_score=True,
n_jobs=-1,
max_features=1,bootstrap_features=True) # 设置取样的特征个数为1,并且取样后放回
random_subspaces_clf.fit(X,y)
random_subspaces_clf.oob_score_
0.83
既针对样本,又针对特征进行随机取样:Random Patches
random_patches_clf = BaggingClassifier(DecisionTreeClassifier(),
n_estimators=500,
max_samples=100, # 数据集样本为500
bootstrap=True,
oob_score=True,
n_jobs=-1,
max_features=1,bootstrap_features=True) # 设置取样的特征个数为1,并且取样后放回
random_patches_clf.fit(X,y)
random_patches_clf.oob_score_
0.856
随机森林与Extra-Trees
随机森林
在使用Bagging对决策树进行创建子模型,形成了由多颗决策树组成的集成模型:
BaggingClassifier(base_estimator=DecisionTreeClassifier())
在机器学习领域称之为随机森林,随机森林也克服了决策树的诸多缺陷比如过拟合等等。
随机森林中的决策树在节点划分时是在随机的特征子集上寻找最优划分特征。
使用随机森林
from sklearn.ensemble import RandomForestClassifier
rf_clf = RandomForestClassifier(n_estimators=500,random_state=666,oob_score=True,n_jobs=-1)
rf_clf.fit(X,y)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=500,
n_jobs=-1, oob_score=True, random_state=666, verbose=0,
warm_start=False)
从控制台打印的随机森林对象参数可以看出,对于随机森林,其参数主要是由决策树与Bagging的超参数构成
rf_clf.oob_score_
0.892
rf_clf2 = RandomForestClassifier(n_estimators=500,random_state=666,oob_score=True,n_jobs=-1,
max_leaf_nodes=16)
rf_clf2.fit(X,y)
rf_clf2.oob_score_
0.906
Extra-Trees
在上述比较normal的随机森林的基础上衍生出了Extra-Trees算法,Extra-Trees同样集成了Bagging与决策树,而她与随机森林的唯一区别在于:
Extra-Trees中的决策树在节点划分时是使用随机的特征和随机的阈值
提供了额外的随机性,抑制过拟合(方差),但增大了bias(偏差)
与此同时由于随机给定划分规则,所以拥有更快的训练速度
使用Extra-Trees
from sklearn.ensemble import ExtraTreesClassifier
et_clf = ExtraTreesClassifier(n_estimators=500,bootstrap=True,oob_score=True,random_state=666)
et_clf.fit(X,y)
ExtraTreesClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=500,
n_jobs=None, oob_score=True, random_state=666, verbose=0,
warm_start=False)
et_clf.oob_score_
0.892
集成学习解决回归问题
from sklearn.ensemble import BaggingRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import ExtraTreesRegressor
boston = datasets.load_boston()
X = boston.data
y = boston.target
X.shape
(506, 13)
BaggingRegressor
from sklearn.tree import DecisionTreeRegressor
bagging_reg = BaggingRegressor(DecisionTreeRegressor(),
n_estimators=500,
max_samples=100,
bootstrap=True,
oob_score=True,
n_jobs=-1)
bagging_reg.fit(X,y)
bagging_reg.oob_score_
0.8378693232167963
RandomForestRegressor
rf_reg = RandomForestRegressor(n_estimators=500,
bootstrap=True,
oob_score=True,
n_jobs=-1)
rf_reg.fit(X,y)
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=500, n_jobs=-1,
oob_score=True, random_state=None, verbose=0,
warm_start=False)
rf_reg.oob_score_
0.8806454682864159
ExtraTreesRegressor
et_reg = ExtraTreesRegressor(n_estimators=500,
bootstrap=True,
oob_score=True,
n_jobs=-1)
et_reg.fit(X,y)
ExtraTreesRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=500, n_jobs=-1,
oob_score=True, random_state=None, verbose=0,
warm_start=False)
et_reg.oob_score_
0.8795443696121401
Boosting
除了Bagging的那种集成方式,在集成学习中还有一类非常重要的集成方式:Boosting
Boosting也是集成多个模型,但是每个模型都在尝试增强(Boosting)整体的效果。
维基百科定义
Boosting(提升算法):是一种可以用来减小监督式学习中偏差的机器学习算法。面对的问题是迈可·肯斯(Michael Kearns)提出的:[1]一组“弱学习者”的**能否生成一个“强学习者”?弱学习者一般是指一个分类器,它的结果只比随机分类好一点点;强学习者指分类器的结果非常接近真值。
Boosting通过在训练新模型实例时更注重先前模型错误分类的实例来增量构建集成模型。在某些情况下Boosting已被证明比Bagging可以得到更好的准确率,不过它也更倾向于对训练数据过拟合。目前比较常见的增强实现有AdaBoost等算法。
大多数Boosting算法包括由迭代使用弱学习分类器组成,并将其结果加入一个最终的成强学习分类器。加入的过程中,通常根据它们的分类准确率给予不同的权重。加和弱学习者之后,数据通常会被重新加权,来强化对之前分类错误数据点的分类。
一个经典的提升算法例子是AdaBoost。一些最近的例子包括LPBoost、TotalBoost、BrownBoost、MadaBoost及LogitBoost。许多提升方法可以在AnyBoost框架下解释为在函数空间利用一个凸的误差函数作梯度下降。
AdaBoost
该算法其实是一个简单的弱分类算法提升过程,这个过程通过不断的训练,可以提高对数据的分类能力。整个过程如下所示:
-
先通过对N个训练样本的学习得到第一个弱分类器;
-
将分错的样本和其他的新数据一起构成一个新的N个的训练样本,通过对这个样本的学习得到第二个弱分类器
-
将1和2都分错了的样本加上其他的新样本构成另一个新的N个的训练样本,通过对这个样本的学习得到第三个弱分类器;
-
最终经过提升的强分类器。即某个数据被分为哪一类要由各分类器权值决定。
由Adaboost算法的描述过程可知,该算法在实现过程中根据训练集的大小初始化样本权值,使其满足均匀分布,在后续操作中通过公式来改变和规范化算法迭代后样本的权值。样本被错误分类导致权值增大,反之权值相应减小,这表示被错分的训练样本集包括一个更高的权重。这就会使在下轮时训练样本集更注重于难以识别的样本,针对被错分样本的进一步学习来得到下一个弱分类器,直到样本被正确分类。在达到规定的迭代次数或者预期的误差率时,则强分类器构建完成。
AdaBoost算法流程
- begin initial D={x1,y1,…,xn,yn}, k m a x k_{max} kmax(最大循环次数), W k ( i ) = 1 / n , i = 1 , . . . , n Wk(i)=1/n,i=1,...,n Wk(i)=1/n,i=1,...,n,
- k ← 0
- do k ← k+1
- 训练使用按照Wk(i)采样的D的弱学习器 C k C_k Ck
- Ek ←对使用Wk(i)的D测量的 C k C_k Ck 的训练误差
- α k ← 1 2 ln 1 − E k E k ! [ α k ← 1 2 ln 1 − E k E k ] {\displaystyle \alpha _{k}\gets {\tfrac {1}{2}}\ln {\frac {1-E_{k}}{E_{k}}}}![\alpha _{{k}}\gets {\tfrac {1}{2}}\ln {\frac {1-E_{{k}}}{E_{{k}}}}] αk←21lnEk1−Ek![αk←21lnEk1−Ek]
- KaTeX parse error: Undefined control sequence: \mbox at position 98: …\alpha _{k}},&{\̲m̲b̲o̲x̲{if }}h_{k}(x^{…
- until k = k m a x k=k_{max} k=kmax
- return C k C_k Ck和 α k α_k αk,k=1,…,kmax(带权值分类器的总体)
- end
使用Ada Boosting
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
from sklearn import datasets
from sklearn.model_selection import train_test_split
X,y = datasets.make_moons(n_samples=500,noise=0.3,random_state=666)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
ada_clf = AdaBoostClassifier(
base_estimator=DecisionTreeClassifier(max_depth=3),
n_estimators=500
)
ada_clf.fit(X_train,y_train)
AdaBoostClassifier(algorithm='SAMME.R',
base_estimator=DecisionTreeClassifier(class_weight=None,
criterion='gini',
max_depth=3,
max_features=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
presort=False,
random_state=None,
splitter='best'),
learning_rate=1.0, n_estimators=500, random_state=None)
ada_clf.score(X_test,y_test)
0.864
Gradient Boosting
之前说的AdaBoost中每一轮基学习器训练过后都会更新样本权重,再训练下一个学习器,最后将所有的基学习器加权组合。AdaBoost使用的是指数损失,这个损失函数的缺点是对于异常点非常敏感,因而通常在噪音比较多的数据集上表现不佳。
Gradient Boosting在这方面进行了改进,使得可以使用任何损失函数 (只要损失函数是连续可导的)这样一些比较robust(健壮)的损失函数就能得以应用,使模型抗噪音能力更强。
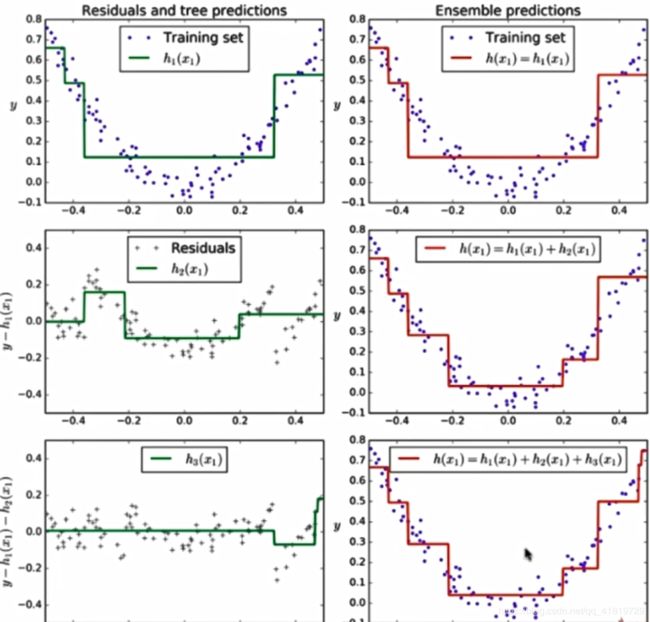
Gradient Boosting工作流程
-
训练一个模型m1,产生错误e1
-
针对e1训练第二个模型m2,产生错误e2
-
针对e2训练第三个模型m3,产生错误e3…
-
最终预测结果是:m1+m2+m3+…
使用Gradient Boosting
from sklearn.ensemble import GradientBoostingClassifier
gb_clf = GradientBoostingClassifier(max_depth=3,n_estimators=30) # Grandient Boosting默认是以决策树为基础模型的
gb_clf.fit(X_train,y_train)
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.1, loss='deviance', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=30,
n_iter_no_change=None, presort='auto',
random_state=None, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0,
warm_start=False)
gb_clf.score(X_test,y_test)
0.888
Stacking
在Voting集成学习机制的基础上,稍作改进就有了一种新的集成学习机制:Stacking
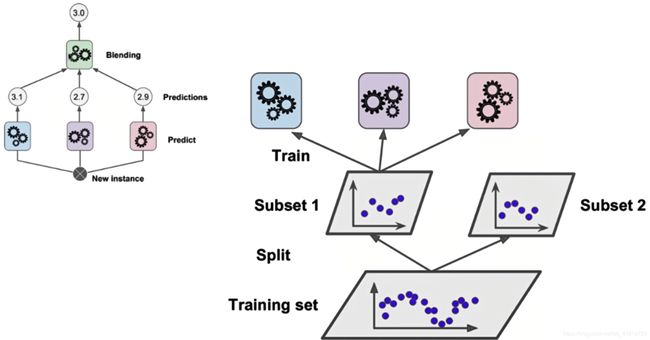
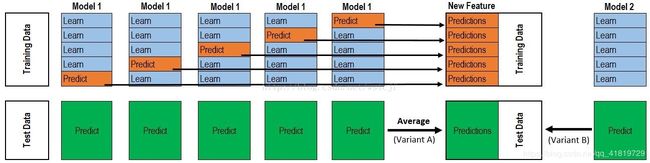
stacking 就是当用初始训练数据学习出若干个base model后,将这些base model的预测结果作为新的训练集,来学习一个新的模型。
下图提供了stacking实现过程更为详细的解释:
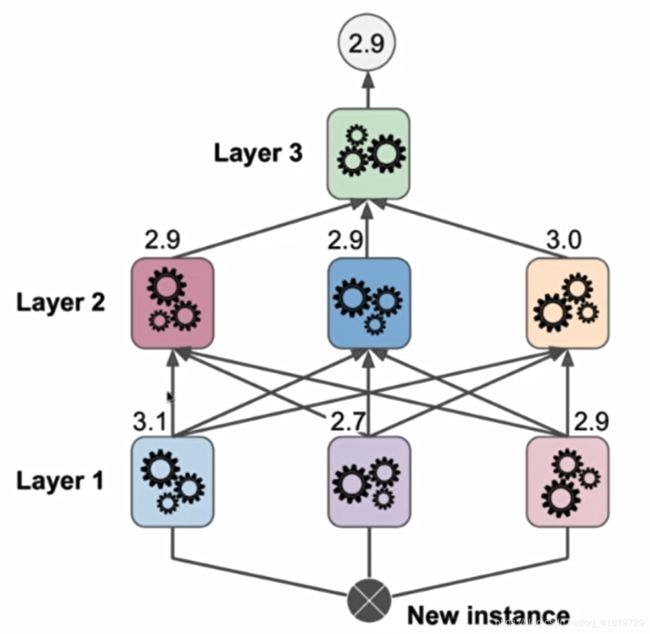
stacking模型可以有多层:
其实Stacking模型非常近似为神经网络,只不过对于神经网络的每一个神经元相应的不是一个全新的算法,而只是计算一个函数的值而已。
Stacking的使用
scikit-learn中并未提供Stacking的相关实现,因而,开发者Artem Golubin在heamy库中实现了Stacking,还提供了许多计算优化,比如缓存等等。
文档:https://heamy.readthedocs.io/en/latest/estimator.html#regressor
总结
集成学习是一种非常强大的学习方法,背后有许多丰富的数学理论基础,也是作为各大机器学习竞赛保命神器,所以还是非常重要滴。
参考致谢
liuyubobo: https://github.com/liuyubobobo/Play-with-Machine-Learning-Algorithms
liuyubobo:https://coding.imooc.com/class/169.html
维基百科:
知乎:https://zhuanlan.zhihu.com/p/41536315