PCL-点云处理(二)
PCL—点云处理(二)
- PCL—低层次视觉—点云分割(最小割算法)
- 1.点云分割的精度
- 2.最小割算法
- 3. 点云 “图”
- 4. PCL对最小割算法的实现
- PCL—点云滤波(基于点云频率)-低
- 1. 点云的频率
- 2. 基于点云频率的滤波方法
- 3. PCL对该算法的实现
- PCL—点云分割(超体聚类)-低
- 1. 超体聚类——一种来自图像的分割方法
- 2. 超体聚类的实现步骤
- 3. PCL对超体聚类的实现
- PCL—点云分割(基于形态学) 低层次点云处理
- 1. 航空测量与点云的形态学
- 2. 三维形态学算子
- 3. PCL对本算法的实现
- PCL—点云分割(基于凹凸性)-低
- 1.图像分割的两条思路
- 2.LCCP方法
- 3. CPC方法
- 3.2 PCL的实现
- PCL—关键点检测(rangeImage)
- 1.关键点,线,面
- 2. 来自点云的降维打击
- 3. 基于PCL的点云-深度图转换
- PCL—关键点检测(NARF)
- 1. 边缘提取
- 2. 关键点提取
- 3. 关于特征点提取的一些思考
- PCL—关键点检测(Harris)
- 1.Harris 算法
- 2. 矩阵的方向性
- 3. 3DHarris
- 4.PCL对Harris算法的实现
- PCL—关键点检测(iss&Trajkovic)
- 1. ISS算法
- 2. Trajkovic关键点检测算法
PCL—低层次视觉—点云分割(最小割算法)
1.点云分割的精度
基于采样一致的点云分割算法显然是意识流的,它只能割出大概的点云(可能是杯子的一部分,但杯把儿肯定没分割出来)。基于欧式算法的点云分割面对有牵连的点云就无力了(比如风筝和人,在不用三维形态学去掉中间的线之前,是无法分割风筝和人的)。基于法线等信息的区域生长算法则对平面更有效,没法靠它来分割桌上的碗和杯子。也就是说,上述算法更关注能不能分割,除此之外,我们还需要一个方法来解决分割的“好不好”这个问题。也就是说,有没有哪种方法,可以在一个点不多,一个点不少的情况下,把目标和“其他”分开。
答案是有,也就是这篇博文要解决的最小割算法。
2.最小割算法
最小割(min-cut)并不是一个什么很新鲜的东西。它早就用在网络规划,求解桥问题,图像分割等领域,被移植到点云分割上也不足为奇。最小割算法是图论中的一个概念,其作用是以某种方式,将两个点分开,当然这两个点中间可能是通过无数的点再相连的。如图所示。
最小割(min-cut)并不是一个什么很新鲜的东西。它早就用在网络规划,求解桥问题,图像分割等领域,被移植到点云分割上也不足为奇。最小割算法是图论中的一个概念,其作用是以某种方式,将两个点分开,当然这两个点中间可能是通过无数的点再相连的。如图所示。

如果要分开最左边的点和最右边的点,红绿两种割法都是可行的,但是红线跨过了三条线,绿线只跨过了两条。单从跨线数量上来论可以得出绿线这种切割方法更优的结论。但假设线上有不同的权值,那么最优切割则和权值有关了。它到底是怎么找到那条绿线的暂且不论。总而言之,就是有那么一个算法,当你给出了点之间的 “图” (广义的),以及连线的权值时,最小割算法就能按照你的要求把图分开。
3. 点云 “图”
显而易见,切割有两个非常重要的因素,第一个是获得点与点之间的拓扑关系,也就是生成一张“图”。第二个是给图中的连线赋予合适的权值。只要这两个要素合适,最小割算法就会办好剩下的事情。点云是一种非常适合分割的对象(我第三次强调这个事情了),点云有天然分开的点。有了点之后,只要把点云中所有的点连起来就可以了。连接算法如下:
1、找到每个点最近的n个点
2、将这n个点和父点连接
3、找到距离最小的两个块(A块中某点与B块中某点距离最小),并连接
4、重复3,直至只剩一个块
现在已经有了“图”,只要给图附上合适的权值,就完成了所有任务。物体分割给人一个直观印象就是属于该物体的点,应该相互之间不会太远。也就是说,可以用点与点之间的欧式距离来构造权值。所有线的权值可映射为线长的函数。
貌似我们现在已经搞定一切了,其实不然。分割总是有一个目标的,而这种精准打击的算法,显然你要告诉我打击对象是谁,打击范围多大——目标需要人为指定(center),尺寸需要提前给出(radius)。
OK,我们现在有了打击对象了(指定了目标物体上的一个点),接下来要做的,就是让除此对象之外的物体被保护起来,不受到打击。保护的方法就是认为加重目标范围之外的权值(罚函数)。
上述过程其实看起来还不够智能,如果有办法让我只需要点一下鼠标,选中要分割的物体,接下来电脑替我操心其他事情,那就太好了。这其实是可以实现的,称为AutoMatic Regime.但PCL并没有封装这个算法,忽略不表。
4. PCL对最小割算法的实现
//生成分割器
pcl::MinCutSegmentation<pcl::PointXYZ> seg;
//分割输入分割目标
seg.setInputCloud (cloud);
//指定打击目标(目标点)
pcl::PointCloud<pcl::PointXYZ>::Ptr foreground_points(new pcl::PointCloud<pcl::PointXYZ> ());
pcl::PointXYZ point;
point.x = 68.97; point.y = -18.55; point.z = 0.57; foreground_points->points.push_back(point); seg.setForegroundPoints (foreground_points);
//指定权函数sigma
seg.setSigma (0.25);
//物体大概范围
seg.setRadius (3.0433856);
//用多少生成图
seg.setNumberOfNeighbours (14);
//和目标点相连点的权值(至少有14个)
seg.setSourceWeight (0.8);
//分割结果
std::vector <pcl::PointIndices> clusters;
seg.extract (clusters);显然,最小割算法更注重分割的精确性而不是分割自动进行。最小割算法用于半自动分割识别有着巨大的优势,适合用于计算机视觉,城市场景点云分析一类。但对机器人来说,或许和特征点检测算法联合起来能获得较好的效果。
图中显示,最小割算法成功找到了靠的很近的汽车。显然欧式算法r取太大则无法区分左右汽车,r取太小则无法区分车头和车身(玻璃不反光,是没有点云的)。
PCL—点云滤波(基于点云频率)-低
1. 点云的频率
点云表达的是三维空间中的一种信息,这种信息本身并没有一一对应的函数值。故点云本身并没有在讲诉一种变化的信号。但在抽象意义上,点云必然是在表达某种信号的,虽然没有明确的时间关系,但应该会存在某种空间关系(例如LiDar点云)。我们可以人为的指定点云空间中的一个点(例如Scan的重心或LiDar的“源”),基于此点来讨论点云在各个方向上所谓的频率。
在传统的信号处理中,高频信号一般指信号变化快,低频信号一般指信号变化缓慢。在图像处理中,高低频的概念被引申至不同方向上图像灰度的变化,傅里叶变换可以用于提取图像的周期成分滤除布纹噪声。在点云处理中,定义:点云法线向量差为点云所表达的信号。换言之,如果某处点云曲率大,则点云表达的是一个变化的信号。如果点云曲率小,则其表达的是一个不变的信号。这和我们的直观感受也是相近的,地面曲率小,它表达的信息量也小;人的五官部分曲率大,其表达了整个Scan中最大的信息量。
2. 基于点云频率的滤波方法
虽然点云频率之前并没有被讨论,但使用频率信息的思想已经被广泛的应用在了各个方面,最著名的莫过于DoN算法。DoN算法被作者归类于点云分割算法中,但我认为并不准确,本质上DoN只是一种前处理,应该算是一种比较先进的点云滤波算法。分割本质上还是由欧式分割算法完成的。DoN 是 Difference of Normal 的简写。算法的目的是在去除点云低频滤波,低频信息(例如建筑物墙面,地面)往往会对分割产生干扰,高频信息(例如建筑物窗框,路面障碍锥)往往尺度上很小,直接采用 基于临近信息 的滤波器会将此类信息合并至墙面或路面中。所以DoN算法利用了多尺度空间的思想,算法如下:
1、在小尺度上计算点云法线1
2、在大尺度上计算点云法线2
3、法线1-法线2
4、滤去3中值较小的点
5、欧式分割
显然,在小尺度上是可以对高频信息进行检测的,此算法可以很好的小尺度高频信息。其在大规模点云(如LiDar点云)中优势尤其明显。
3. PCL对该算法的实现
算法实现过程可表示为:
// Create a search tree, use KDTreee for non-organized data.
pcl::search::Search<PointXYZRGB>::Ptr tree;
if (cloud->isOrganized ())
{
tree.reset (new pcl::search::OrganizedNeighbor<PointXYZRGB> ());
}else
{
tree.reset (new pcl::search::KdTree<PointXYZRGB> (false));
}
// Set the input pointcloud for the search tree
tree->setInputCloud (cloud);
//生成法线估计器(OMP是并行计算,忽略)
pcl::NormalEstimationOMP<PointXYZRGB, PointNormal> ne;ne.setInputCloud (cloud);
ne.setSearchMethod (tree);
//设定法线方向(要做差,同向很重要)
ne.setViewPoint (std::numeric_limits<float>::max (), std::numeric_limits<float>::max (), std::numeric_limits<float>::max ());
//计算小尺度法线
pcl::PointCloud<PointNormal>::Ptr normals_large_scale (new pcl::PointCloud<PointNormal>); ne.setRadiusSearch (scale2); ne.compute (*normals_large_scale);
//计算大尺度法线
pcl::PointCloud<PointNormal>::Ptr normals_large_scale (new pcl::PointCloud<PointNormal>); ne.setRadiusSearch (scale2); ne.compute (*normals_large_scale);
//生成DoN分割器
pcl::DifferenceOfNormalsEstimation<PointXYZRGB, PointNormal, PointNormal> don; don.setInputCloud (cloud); don.setNormalScaleLarge (normals_large_scale); don.setNormalScaleSmall (normals_small_scale);
//计算法线差
PointCloud<PointNormal>::Ptr doncloud (new pcl::PointCloud<PointNormal>); copyPointCloud<PointXYZRGB, PointNormal>(*cloud, *doncloud); don.computeFeature (*doncloud);
//生成滤波条件:把法线差和阈值比
pcl::ConditionOr<PointNormal>::Ptr range_cond (new pcl::ConditionOr<PointNormal> () );range_cond->addComparison (pcl::FieldComparison<PointNormal>::ConstPtr (new pcl::FieldComparison<PointNormal> ("curvature", pcl::ComparisonOps::GT, threshold)) );
//生成条件滤波器,输入滤波条件和点云
pcl::ConditionalRemoval<PointNormal> condrem (range_cond); condrem.setInputCloud (doncloud);
//导出滤波结果
pcl::PointCloud<PointNormal>::Ptr doncloud_filtered (new pcl::PointCloud<PointNormal>); condrem.filter (*doncloud_filtered);
//欧式聚类PCL—点云分割(超体聚类)-低
参考博客:https://www.bbsmax.com/A/nAJvX6gwdr/
1. 超体聚类——一种来自图像的分割方法
超体(supervoxel)是一种集合,集合的元素是“体”。与体素滤波器中的体类似,其本质是一个个的小方块。与之前提到的所有分割手段不同,超体聚类的目的并不是分割出某种特定物体,其对点云实施过分割(over segmentation),将场景点云化成很多小块,并研究每个小块之间的关系。这种将更小单元合并的分割思路已经出现了有些年份了,在图像分割中,像素聚类形成超像素,以超像素关系来理解图像已经广为研究。本质上这种方法是对局部的一种总结,纹理,材质,颜色类似的部分会被自动的分割成一块,有利于后续识别工作。比如对人的识别,如果能将头发,面部,四肢,躯干分开,则能更好的对各种姿态,性别的人进行识别。
点云和图像不一样,其不存在像素邻接关系。所以,超体聚类之前,必须以八叉树对点云进行划分,获得不同点团之间的邻接关系。与图像相似点云的邻接关系也有很多,如面邻接,线邻接,点邻接。其具体解释如下图:
2. 超体聚类的实现步骤
举个简单的例子来体会下超体聚类,其过程和结晶类似。但不是水结晶成冰,而是盐溶液过饱和状态下的多晶核结晶。所有的晶核(seed)同时开始生长,最终填满整个空间,使物质具有晶体结构。 超体聚类实际上是一种特殊的区域生长算法,和无限制的生长不同,超体聚类首先需要规律的布置区域生长“晶核”。晶核在空间中实际上是均匀分布的,并指定晶核距离(Rseed)。再指定粒子距离(Rvoxel)。再指定最小晶粒(MOV),过小的晶粒需要融入最近的大晶粒。关系如图所示:

有了晶粒和结晶范围之后,我们只需要控制结晶过程,就能将整个空间划分开了。结晶过程的本质就是不断吸纳类似的粒子(八分空间)。类似是一个比较模糊的概念,关于类似的定义有以下公式:

公式中的Dc,表示颜色上的差异,Dn表示法线上的差异,Ds代表点距离上的差异。w_*表示一系列权重。用于控制结晶形状。在晶核周围寻找一圈,D最小的体素被认为是下一个“被发展的党员”。需要注意的是,结晶过程并不是长完一个晶核再长下一个,二是所有的晶核同时开始生长(虽然计算机计算时必然有先后,但从层次上来说是同时的)。其生长顺序如下图所示:
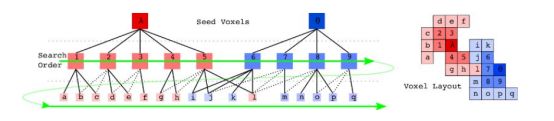
接下来所有晶核继续公平竞争,发展第二个“党员”,以此循环,最终所有晶体应该几乎同时完成生长。整个点云也被晶格所分割开来。并且保证了一个晶包里的粒子都是类似的。
3. PCL对超体聚类的实现
//设定结晶参数
float voxel_resolution = 0.008f;
float seed_resolution = 0.1f;
float color_importance = 0.2f;
float spatial_importance = 0.4f;
float normal_importance = 1.0f;
//生成结晶器
pcl::SupervoxelClustering<PointT> super (voxel_resolution, seed_resolution);
//和点云形式有关
if (disable_transform)
super.setUseSingleCameraTransform (false);
//输入点云及结晶参数
super.setInputCloud (cloud);
super.setColorImportance (color_importance);
super.setSpatialImportance (spatial_importance);
super.setNormalImportance (normal_importance);
//输出结晶分割结果:结果是一个映射表
std::map <uint32_t, pcl::Supervoxel<PointT>::Ptr > supervoxel_clusters;super.extract (supervoxel_clusters);
//获得晶体中心
PointCloudT::Ptr voxel_centroid_cloud = super.getVoxelCentroidCloud ();
//获得晶体
PointLCloudT::Ptr labeled_voxel_cloud = super.getLabeledVoxelCloud ();执行上诉过程后,会将晶体映射成一系列数。数代表的是指向各个晶体的指针。可以通过getter函数,把晶体有关的信息拖出来。拖出来的是点云。
//将相连的晶体中心连起来并显示
std::multimap<uint32_t, uint32_t> supervoxel_adjacency;super.getSupervoxelAdjacency (supervoxel_adjacency);std::multimap<uint32_t,uint32_t>::iterator label_itr = supervoxel_adjacency.begin ();
for ( ; label_itr != supervoxel_adjacency.end (); )
{
//First get the label
uint32_t supervoxel_label = label_itr->first;
//Now get the supervoxel corresponding to the label
pcl::Supervoxel<PointT>::Ptr supervoxel = supervoxel_clusters.at (supervoxel_label);
//Now we need to iterate through the adjacent supervoxels and make a point cloud of themPointCloudT
adjacent_supervoxel_centers;std::multimap<uint32_t,uint32_t>::iterator adjacent_itr = supervoxel_adjacency.equal_range (supervoxel_label).first;for ( ; adjacent_itr! =supervoxel_adjacency.equal_range (supervoxel_label).second; ++adjacent_itr){pcl::Supervoxel<PointT>::Ptr neighbor_supervoxel = supervoxel_clusters.at (adjacent_itr->second);adjacent_supervoxel_centers.push_back (neighbor_supervoxel->centroid_);}
//Now we make a name for this polygon
std::stringstream ss;ss << "supervoxel_" << supervoxel_label;
//This function is shown below, but is beyond the scope of this tutorial - basically it just generates a "star" polygon mesh from the points givenaddSupervoxelConnectionsToViewer
(supervoxel->centroid_, adjacent_supervoxel_centers, ss.str (), viewer);
//Move iterator forward to next
labellabel_itr = supervoxel_adjacency.upper_bound (supervoxel_label);}至此,生成了不同的晶体之间的邻接关系。结果如下所示(不同晶核距离0.1m,0.05m)

此方法主要为识别做前期准备,但我认为,这种东西用在三维视觉+有限元倒是极好的。可以在不使用应变片的前提下对物体各个部分应变进行直接测量。在已知力的情况下可以建立物体刚度和应变的关系,貌似钢包回转台的手里分析可以这样解决。蛋疼的是实际工业机械哪有那么多花花绿绿的给你分割,很难形成有效的对应点匹配。
PCL—点云分割(基于形态学) 低层次点云处理
1. 航空测量与点云的形态学
航空测量是对地形地貌进行测量的一种高效手段。生成地形三维形貌一直是地球学,测量学的研究重点。但对于城市,森林,等独特地形来说,航空测量会受到影响。因为土地表面的树,地面上的房子都认为的改变了地貌,可以认为是地貌上的噪声点。设计一种有效的手段去除地面噪声对地形测量的影响显得非常重要。这种工作可以认为是一种特殊的点云分割,一般情况下点云分割的目标是去除地面,而这种方法需要在不使用地面平整假设的前提下获得地面。
形态学是图像处理中非常重要的概念,对二值图像而言,可由简单的膨胀运算和腐蚀运算组成一个完整的图像处理族。但是想要将这个算法移植到三维点云上是比较难的,首先一般的点云没有明显的映射值,也没有清晰的定义域,很难设计形态学处理的基理。但是LIDAR点云例外。由于LIDAR点云由飞机获得,飞机距离地面相对较远,且测量方向和地面垂直。这就形成了比较完整的xy->z映射(z方向的范围远远小于xy方向),z方向代表地面物体的高度,x,y方向为平行与地面且相互垂直的两个轴。有了明确的定义域以及单值映射关系就有了设计形态学算法的基本要素。实际上除了形态学算法之外,许多图像处理算法都可以用来分割LIDAR点云了,本质上这就是一幅大图像。
2. 三维形态学算子
对于图像而言,形态学运算一般是针对二值图像而言的。当然也有针对灰度的形态学运算,其原理应该和针对点云的形态学运算类似(我猜的)。形态学算子的设计实际上非常简单,只要能设计出基础的膨胀和腐蚀算子就可以组合得到一系列的处理。

其中,d表示膨胀算子,e表示腐蚀算子。算子的原理有些像中值滤波,通过选取一个窗w中最高点或最低点来完成图像的膨胀和腐蚀,其效果如下图所示:
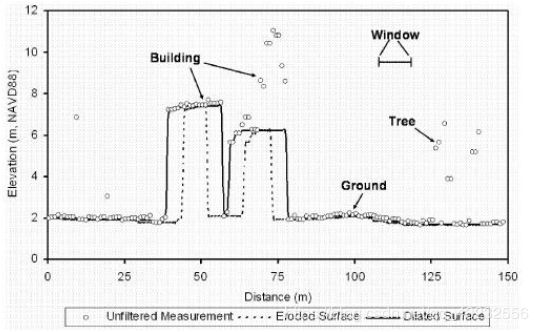
在航拍图的横截面上可以很清楚的看出膨胀与腐蚀的效果。对于房子和树可以用不同尺度窗(从小到大)先腐蚀至地面。但是这会导致一个巨大的问题。。。如果地面上有个土包(比如秦始皇陵),那么这个土包也会在一次次的腐蚀中被消耗。那岂不是秦始皇陵就发现不了?所以还有一个补偿算法用于解决这个问题,称为线性补偿算法。
建筑物和土包有一个巨大的区别,建筑物往往相对比较陡峭,而土包却是变化比较平缓的。这个可以作为一个判据,用于判断物体是否需要被腐蚀,也作为窗收敛的判据。wk = 2kb + 1
式中k称为斜率,代表下一个窗的大小是上一个窗的2^k倍
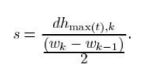
s是一个因子
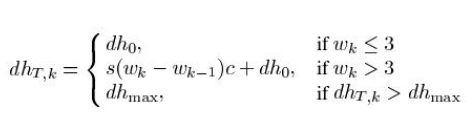
dh是切深判据,每一次腐蚀大于切深判据才认为是有效的,小于切深判据则是土包。所有材料都被收录于文章:A Progressive Morphological Filter for Removing Nonground Measurements From Airborne LIDAR Data
3. PCL对本算法的实现
//生成形态滤波器
pcl::ProgressiveMorphologicalFilter<pcl::PointXYZ> pmf; pmf.setInputCloud (cloud);
//设置窗的大小以及切深,斜率信息
pmf.setMaxWindowSize (20);
pmf.setSlope (1.0f);
pmf.setInitialDistance (0.5f);
pmf.setMaxDistance (3.0f);
//提取地面
pmf.extract (ground->indices);
// 从标号到点云
pcl::ExtractIndices<pcl::PointXYZ> extract;
extract.setInputCloud (cloud);
extract.setIndices (ground);
extract.filter (*cloud_filtered);PCL—点云分割(基于凹凸性)-低
1.图像分割的两条思路
场景分割时机器视觉中的重要任务,尤其对家庭机器人而言,优秀的场景分割算法是实现复杂功能的基础。但是大家搞了几十年也还没搞定——不是我说的,是接下来要介绍的这篇论文说的。图像分割的搞法大概有两种:剑宗——自低向上:先将图像聚类成小的像素团再慢慢合并,气宗——自顶向下:用多尺度模板分割图像,再进一步将图像优化分割成不同物体。当然,还有将二者合而为一的方法:training with data set. 这第三种方法也不好,太依赖于已知的物体而失去了灵活性。家庭机器人面对家里越来越多的东西需要一种非训练且效果很好的分割法。 Object Partitioning using Local Convexity 一文的作者从古籍中(也不老,1960s左右吧),找到了一种基于凹凸性的分割方法。实际上基于凹凸的图像理解在之前是被研究过的,但是随着神经网络的出现,渐渐这种从明确物理意义入手的图像"理解"方法就被淹没了。对于二维图像而言,其凹凸性较难描述,但对于三维图像而言,凹凸几乎是与生俱来的性质。
2.LCCP方法
LCCP是Locally Convex Connected Patches的缩写,翻译成中文叫做 ”局部凸连接打包一波带走“~~~算法大致可以分成两个部分:1.基于超体聚类的过分割。2.在超体聚类的基础上再聚类。超体聚类作为一种过分割方法,在理想情况下是不会引入错误信息的,也就是说适合在此基础上再进行处理。关于超体聚类相关内容见我的博文:超体聚类。 LCCP方法并不依赖于点云颜色,所以只使用空间信息和法线信息,wc=0。ws=1,wn=4。
2.1算法理论
点云完成超体聚类之后,对于过分割的点云需要计算不同的块之间凹凸关系。凹凸关系通过 CC(Extended Convexity Criterion) 和 SC (Sanity criterion)判据来进行判断。其中 CC 利用相邻两片中心连线向量与法向量夹角来判断两片是凹是凸。显然,如果图中a1>a2则为凹,反之则为凸。

考虑到测量噪声等因素,需要在实际使用过程中引入门限值(a1需要比a2大出一定量)来滤出较小的凹凸误判。此外,为去除一些小噪声引起的误判,还需要引入“第三方验证”,如果某块和相邻两块都相交,则其凹凸关系必相同。CC 判据最终如CCe:

如果相邻两面中,有一个面是单独的,cc判据是无法将其分开的。举个简单的例子,两本厚度不同的书并排放置,视觉算法应该将两本书分割开。如果是台阶,则视觉算法应该将台阶作为一个整体。本质上就是因为厚度不同的书存在surface-singularities。为此需要引入SC判据,来对此进行区分。
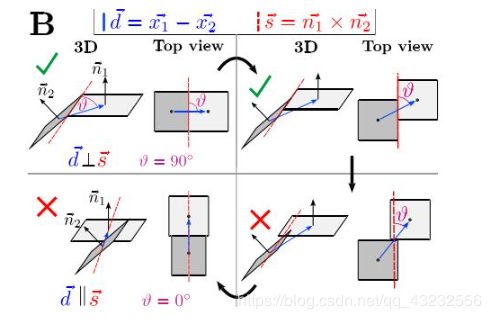
如图所示,相邻两面是否真正联通,是否存在单独面,与θ角有关,θ角越大,则两面真的形成凸关系的可能性就越大。据此,可以设计SC判据:

其中S(向量)为两平面法向量的叉积。最终,两相邻面之间凸边判据为:

在标记完各个小区域的凹凸关系后,则采用区域增长算法将小区域聚类成较大的物体。此区域增长算法受到小区域凹凸性限制。只允许区域跨越凸边增长。
至此,分割完成,在滤去多余噪声后既获得点云分割结果。此外:考虑到RGB-D图像随深度增加而离散,难以确定八叉树尺寸,故在z方向使用对数变换以提高精度。分割结果如图:


从图中可知,纠缠在一起,颜色形状相近的物体完全被分割开了,如果是图像分割要达到这个效果,那就比较难了。
2.2 PCL的实现
1.超体聚类
//设定结晶参数
float voxel_resolution = 0.008f; float seed_resolution = 0.1f; float color_importance = 0.2f; float spatial_importance = 0.4f; float normal_importance = 1.0f;
//生成结晶器
pcl::SupervoxelClustering<PointT> super (voxel_resolution, seed_resolution);
//和点云形式有关
if (disable_transform)
super.setUseSingleCameraTransform (false);
//输入点云及结晶参数
super.setInputCloud (cloud);
super.setColorImportance (color_importance); super.setSpatialImportance (spatial_importance); super.setNormalImportance (normal_importance);
//输出结晶分割结果:结果是一个映射表
std::map <uint32_t, pcl::Supervoxel<PointT>::Ptr > supervoxel_clusters; super.extract (supervoxel_clusters); std::multimap<uint32_t, uint32_t> supervoxel_adjacency; super.getSupervoxelAdjacency (supervoxel_adjacency);- LCCP
//生成LCCP分割器
pcl::LCCPSegmentation<PointT>::LCCPSegmentation LCCPseg;
//输入超体聚类结果
seg.setInputSupervoxels(supervoxel_clusters,supervoxel_adjacency);
//CC效验beta值
seg.setConcavityToleranceThreshold (concavity_tolerance_threshold);
//CC效验的k邻点
seg.setKFactor (k_factor_arg)seg.setSmoothnessCheck (bool_use_smoothness_check_arg,voxel_res_arg,seed_res_arg,smoothness_threshold_arg = 0.1);
//SC效验
seg.setSanityCheck (bool_use_sanity_criterion_arg);
//最小分割尺寸
seg.setMinSegmentSize (min_segment_size_arg)seg.segment();
seg.relabelCloud (pcl::PointCloud<pcl::PointXYZL> &labeled_cloud_arg);综上所述,LCCP算法在相似物体场景分割方面有着较好的表现,对于颜色类似但棱角分明的物体可使用该算法。(比如X同学仓库里那一堆纸箱)
3. CPC方法
CPC方法的全称为Constrained Planar Cuts,出自论文:Constrained Planar Cuts - Object Partitioning for Point Clouds 。和LCCP方法不同,此方法的分割对象是object。此方法能够将物体分成有意义的块:比如人的肢体等。CPC方法可作为AI的前处理,作为RobotVision还是显得有些不合适。但此方法不需要额外训练,自底向上的将三维图像分割 成有明确意义部分,是非常admirable的。3.1 CPC方法原理
和其他基于凹凸性的方法相同,本方法也需要先进行超体聚类。在完成超体聚类之后,采用和LCCP相同的凹凸性判据获得各个块之间的凹凸关系。在获得凹凸性之后,CPC方法所采取的措施是不同的。其操作称为 半全局分割 。
在分割之前,首先需要生成 EEC(Euclidean edge cloud), EEC的想法比较神奇,因为凹凸性定义在相邻两个”片“上,换言之,定义在连接相邻两“片”的edge上。将每个edge抽象成一个点云,则得到了附带凹凸信息的点云。如图所示,左图是普通点云,但附带了邻接和凹凸信息。右边是EEC,对凹边赋权值1,其他为0。
此方法称作 weighted RanSac

显而易见,某处如果蓝色的点多,那么就越 凹,就越应该切开(所谓切开实际上是用平面划分)。问题就转化为利用蓝点求平面了。利用点云求一个最可能的平面当然需要请出我们的老朋友 RanSaC . 但此处引入一个评价函数,用于评价此次分割的 优良程度Sm,Pm 是EEC中的点.
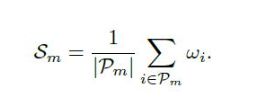
单纯的weighted RanSac算法并不够。其会导致对某些图形的错误分割,所以作者对此做了第一次“修补".错误的分割如下图所示
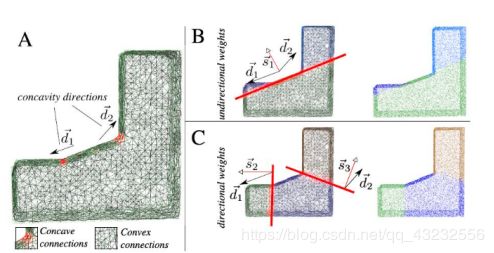
此修补方法称作 directional weighted RanSac
方法的原理很简单,垂直于凹边表面的点具有更高的权重,显然,对于EEC中的凹点,只要取其少量邻点即可估计垂直方向。
这种修补后还有一个问题,如果这个分割面过长的情况下,有可能会误伤。如图所示:
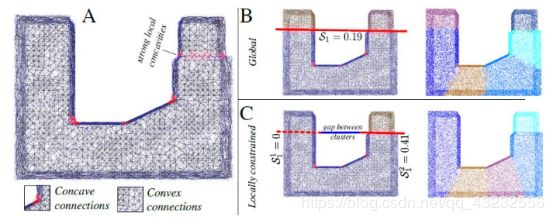
于是有了第二种修补方法,称为:Locally constrained cutting
这种修补方法的原理就更加简单粗暴了,对凹点先进行欧式分割(限制增长上限),之后再分割所得的子域里进行分割。在修修补补之后,CPC算法终于可以投入使用了,从测试集的结果来看,效果还是很好的。
3.2 PCL的实现
在PCL中CPC类继承自 LCCP 类,但是这个继承我觉得不好,这两个类之间并不存在抽象与具体的关系,只是存在某些函数相同而已。不如多设一个 凹凸分割类 作为CPC类与LCCP类的父类,所有的输入接口等都由凹凸分割类提供。由CPC算法和LCCP算法继承凹凸类,作为 凹凸分割 的具体实现。毕竟和 凹凸分割 有关的算法多半是对整体进行分割,和其他点云分割算法区别较大。
//生成CPC分割器
pcl::CPCSegmentation<PointT>::CPCSegmentation seg;
//输入超体聚类结果
seg.setInputSupervoxels(supervoxel_clusters,supervoxel_adjacency);
//设置分割参数
setCutting (max_cuts = 20,
cutting_min_segments = 0,
cutting_min_score = 0.16,
locally_constrained = true,
directed_cutting = true,
clean_cutting = false);
seg.setRANSACIterations (ransac_iterations);
seg.segment();
seg.relabelCloud (pcl::PointCloud<pcl::PointXYZL> &labeled_cloud_arg);PCL—关键点检测(rangeImage)
关键点又称为感兴趣的点,是低层次视觉通往高层次视觉的捷径,抑或是高层次感知对低层次处理手段的妥协。
1.关键点,线,面
关键点=特征点;
关键线=边缘;
关键面=foreground;
上述三个概念在信息学中几乎占据了统治地位。比如1维的函数(信号),有各种手段去得到某个所谓的关键点,有极值点,拐点…二维的图像,特征点提取算法是标定算法的核心(harris),边缘提取算法更是备受瞩目(canny,LOG…),当然,对二维的图像也有区域所谓的前景分割算法用于提取感兴趣的区域,但那属于较高层次的视觉,本文不讨论。 由此可以推断,三维视觉应该同时具备:关键点,关键线,关键面三种算法。本质上,关键面算法就是我们之前一文中讨论的分割算法(三维点云不是实心的)。关于关键点更多的信息可以参考:特征检测。
ok,在这里我们了解到了,要在n维信息中提取n-1维信息是简单的,但n-2维信息会比n-1维要不稳定或者复杂的多。很容易想象,图像的边缘处理算法所得到的结果一般大同小异,但关键点提取算法的结果可以是千差万别的。主要原因是降维过大后,特征的定义很模糊,很难描述清楚对一幅图像来说,到底怎样的点才是关键点。所以,对3维点云来说,关键点的描述就更难了。点云也有1维边缘检测算法,本文不做讨论。单说说关键点提取。
2. 来自点云的降维打击
图像的Harris角点算子将图像的关键点定义为角点。角点也就是物体边缘的交点,harris算子利用角点在两个方向的灰度协方差矩阵响应都很大,来定义角点。既然关键点在二维图像中已经被成功定义且使用了,看来在三维点云中可以沿用二维图像的定义…不过今天要讲的是另外一种思路,简单粗暴,直接把三维的点云投射成二维的图像不就好了。这种投射方法叫做range_image.
首先放上一张range_imge和点云图像的合照:

看起来像个眼睛的那玩意就是range_image. 至于它为什么像个眼睛,就要从它的出生开始说起了。三维点云有多种采集方式,最为著名的是结构光,飞秒相机,双目视觉。简而言之,采集都离不开相机。用相机拍照当然就存在相机的光心坐标原点 Oc 以及主光轴方向 Z. 从这个点,有一种办法可以将三维数据映射到2维平面上。首先,将某点到光心Oc的距离映射成深度图的灰度或颜色(灰度只有256级但颜色却可接近连续变化)。除此之外,再定义一下怎样将点云映射到图像的横纵坐标上就可以了。
任意一点都要和光心进行连线…这么听起来很熟悉…好像有点像球坐标的意思。球坐标长下面这张图这样。在数学里,球坐标系(英语:Spherical coordinate system)是一种利用球坐标(r, θ,φ)表示一个点 p 在三维空间的位置的三维正交坐标系。右图显示了球坐标的几何意义:原点与点 P 之间的径向距离 r ,原点到点 P 的连线与正 z-轴之间的天顶角θ,以及原点到点 P 的连线,在 xy-平面的投影线,与正 x-轴之间的方位角φ 。
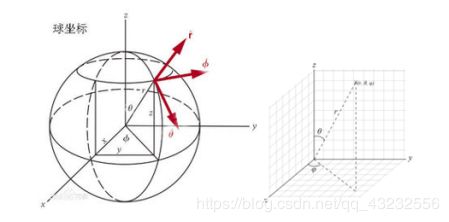
深度图中的横,纵坐标实际上是θ和φ,如果要保证沿着场景中某条直线移动,φ线性变化θ却先增大后减小。这也就造成了深度图像一个眼睛一样。但这并不妨碍什么,φ没有定义的地方可以使用深度无限大来代替。
这样做显然是有好处的,首先,这是一种除了八叉树,kd_tree之外,能够将点云的空间关系表达出来的手段。每个点云都有了横,纵,深,三个坐标,并且这种坐标原点的设定方式,在理论上是不会存在干涉的(从原点出发的一条线理论上不会遇到多余1个点)。于是点云的空间关系就自然的被编码与深度图中。
显然,图像中的关键点检测算子就可以被移植到点云特征点求取中来了。
3. 基于PCL的点云-深度图转换
//rangeImage也是PCL的基本数据结构
pcl::RangeImage rangeImage;
//角分辨率
float angularResolution = (float) ( 1.0f * (M_PI/180.0f));
// 1.0 degree in radians
//phi可以取360°
float maxAngleWidth = (float) (360.0f * (M_PI/180.0f));
// 360.0 degree in radians
//a取180°
float maxAngleHeight = (float) (180.0f * (M_PI/180.0f));
// 180.0 degree in radians
//半圆扫一圈就是整个图像了
//传感器朝向
Eigen::Affine3f sensorPose = (Eigen::Affine3f)Eigen::Translation3f(0.0f, 0.0f, 0.0f);
//除了三维相机模式还可以选结构光模式
pcl::RangeImage::CoordinateFrame coordinate_frame = pcl::RangeImage::CAMERA_FRAME;
//noise level表示的是容差率,因为1°X1°的空间内很可能不止一个点,noise level = 0则表示去最近点的距离作为像素值,如果=0.05则表示在最近点及其后5cm范围内求个平均距离
float noiseLevel=0.00;
//minRange表示深度最小值,如果=0则表示取1°X1°的空间内最远点,近的都忽略
float minRange = 0.0f;
//bordersieze表示图像周边点
int borderSize = 1;
//基本数据结构直接打印是ok的
std::cout << rangeImage << "\n";PCL—关键点检测(NARF)
关键点检测本质上来说,并不是一个独立的部分,它往往和特征描述联系在一起,再将特征描述和识别、寻物联系在一起。关键点检测可以说是通往高层次视觉的重要基础。但本章节仅在低层次视觉上讨论点云处理问题,故所有讨论都在关键点检测上点到为止。NARF 算法实际上可以分成两个部分,第一个部分是关键点提取,第二个部分是关键点信息描述,本文仅涉及第一个部分。
在文章开始之前,有非常重要的一点要说明,点云中任意一点,都有一定概率作为关键点。关键点也是来自原始点云中的一个元素。和图像的边缘提取或者关键点检测算法追求n次插值,最终求的亚像素坐标不同,点云的关键点只在乎找到那个点。
1. 边缘提取
首先声明本文所有思想算法公式均来自:Point Feature Extraction on 3D Range Scans Taking into Account Object Boundaries
在正式开始关键点提取之前,有必要先进行边缘提取。原因是相对于其他点,边缘上的点更有可能是关键点。和图像的边缘不同(灰度明显变化),点云的边缘有更明确的物理意义。对点云而言,场景的边缘代表前景物体和背景物体的分界线。所以,点云的边缘又分为三种:前景边缘,背景边缘,阴影边缘。
rangeImage 是一个天然适合用于边缘提取的框架。在这里需要做一些假设:每个rangeImage像素中假设都只有一个点(显然在生成rangeImage的时候点云是被压缩了的,压缩了多少和rangeImage的分辨率有关,分辨率不能太小,否则rangeImage上会有"洞”,分辨率太大则丢失很多信息)。
三维点云的边缘有个很重要的特征,就是点a 和点b 如果在 rangImage 上是相邻的,然而在三维距离上却很远,那么多半这里就有边缘。由于三维点云的规模和稀疏性,“很远”这个概念很难描述清楚。到底多远算远?这里引入一个横向的比较是合适的。这种比较方法可以自适应点云的稀疏性。所谓的横向比较就是和 某点周围的点相比较。 这个周围有多大?不管多大,反正就是在某点pi的rangeImage 上取一个方窗。假设像素边长为s. 那么一共就取了s^2个点。接下来分三种情况来讨论所谓的边缘:
1.这个点在某个平面上,边长为 s 的方窗没有涉及到边缘
2.这个点恰好在某条边缘上,边长 s 的方窗一半在边缘左边,一半在右边
3.这个点恰好处于某个角点上,边长 s 的方窗可能只有 1/4 与 pi 处于同一个平面
如果将 pi 与不同点距离进行排序,得到一系列的距离,d0 表示与 pi 距离最近的点,显然是 pi 自己。 ds^2 是与pi 最远的点,这就有可能是跨越边缘的点了。 选择一个dm,作为与m同平面,但距离最远的点。也就是说,如果d0~ds^2是一个连续递增的数列,那么dm可以取平均值。如果这个数列存在某个阶跃跳动(可能会形成类似阶跃信号)那么则发生阶跃的地方应该是有边缘存在,不妨取阶跃点为dm(距离较小的按个阶跃点)原文并未如此表述此段落,原文取s=5, m=9 作为m点的一个合理估计。
对任意一个点,进行打分,来判断该点作为边缘点有多大可能性。首先,边缘可能会在某点的:上,下,左,右四个方向。
所以只要把pi 和 pi 右边的点求相对距离。 并把这个相对距离和dm进行比较,就可以判断边缘是不是在该点右边。如果距离远大于dm,显然该点右边的邻点就和pi不是同一个平面了。
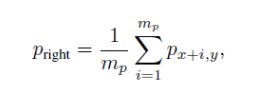
为了增加对噪声的适应能力,取右边的点为右边几个点的平均数。接下来依据此信息对该点进行打分。
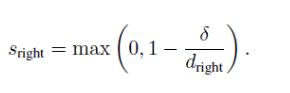
其中deta 就是dm. dright = || pi pright ||. 最后再取大于0.8的Sright,并进行非极大值抑制。就可以得到物体的边缘了。
2. 关键点提取
在提取关键点时,边缘应该作为一个重要的参考依据。但一定不是唯一的依据。对于某个物体来说关键点应该是表达了某些特征的点,而不仅仅是边缘点。所以在设计关键点提取算法时,需要考虑到以下一些因素:
i) it must take information about borders and the surface structure into account;边缘和曲面结构都要考虑进去
ii) it must select positions that can be reliably detected even if the object is observed from another perspective; 关键点要能重复
iii) the points must be on positions that provide stable areas for normal estimation or the descriptor calculation in general.关键点最好落在比较稳定的区域,方便提取法线
对于点云构成的曲面而言,某处的曲率无疑是一个非常重要的结构描述因素。某点的曲率越大,则该点处曲面变化越剧烈。在2D rangeImage 上,去 pi 点及其周边与之距离小于2deta的点,进行PCA主成分分析。可以得到一个 主方向v,以及曲率值 lamda. 注意, v 必然是一个三维向量。
那么对于边缘点,可以取其 权重 w 为1 , v 为边缘方向。
对于其他点,取权重 w 为 1-(1-lamda)^3 , 方向为 v 在平面 p上的投影。 平面 p 垂直于 pi 与原点连线。
到此位置,每个点都有了两个量,一个权重,一个方向。将权重与方向带入下列式子 I 就是某点 为特征点的可能性。

最后进行极大值抑制,就可以得到一些特征点了。
3. 关于特征点提取的一些思考
点云的特征点提取应该与后面的特征描述是松耦合的。确实不得不承认,针对不同的点云:稀疏的,致密的,有序的,无序的,有遮挡的,高精测量的…设计不同的关键点提取算法也无可厚非。总结出的关键点提取算法原则就是要尺度不变,鲁棒性好,至于是否一定要存在于平坦区域,我觉得并不一定。不同的关键点提取算法可以和不同的特征描述算法进行组合,最终得到一个较好的效果。如果非要把关键点提取算法和特征描述算法紧耦合,那势必会失去一部分灵活性。
最后还有一点想要吐槽的是,点云中的点为什么不应该自带是否是关键点的性质,而需要我们来进行检测?这显然不符合面向对象的设计原则…我觉的应该有某种点云采集方法,得到的点云可以有以下性质:point.is_key_point = 1/0.
PCL—关键点检测(Harris)
除去NARF这种和特征检测联系比较紧密的方法外,一般来说特征检测都会对曲率变化比较剧烈的点更敏感。Harris算法是图像检测识别算法中非常重要的一个算法,其对物体姿态变化鲁棒性好,对旋转不敏感,可以很好的检测出物体的角点。甚至对于标定算法而言,HARRIS角点检测是使之能成功进行的基础。
HARRIS算法的思想还是很有意思的。很聪明也很trick.
1.Harris 算法
其思想及数学推导大致如下:
1.在图像中取一个窗 w (矩形窗,高斯窗,XX窗,各种窗,某师姐要改标定算法不就可以从选Harris的窗开始做起么。。。。。)
2.获得在该窗下的灰度 I
3.移动该窗,则灰度会发生变化,平坦区域灰度变化不大,边缘区域沿边缘方向灰度变化剧烈,角点处各个方向灰度变化均剧烈
4.依据3中条件选出角点
当然啦,如果Harris算子的实现也和它的思想这么平淡那我就不表扬他聪明了,Harris算子的具体实现方法,利用的是图像偏微分方程的思想。
先给出抽象数学表达式(不要问我为什么这么淡,我也不知道):
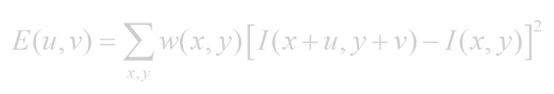
其中 w 代表窗函数,某个x,y为图像坐标,u,v是一个移动向量(既反应移动方向,也反应移动大小)
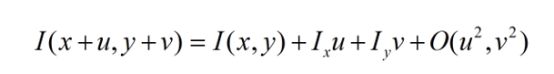
Ix表示图像沿x方向的差分,Iy表示图像沿y方向的差分。图像差分算子有什么SoberPXX总之很多就对了,一阶差分还是很好求的。

显然,E(u,v)可以用另外一种形式来表示了。最终可以表达为协方差矩阵的形式。

在这里我们有了数学中最优雅的表达——Matrix,especially symmetric Matrix. Nothing is better than that.

2. 矩阵的方向性
显然,E(u,v)的值和u,v有关。。。很有关。。
1.可以取一组u,v,让E(u,v)的值最小。
2.还可以取一组u,v,让E(u,v)的值最大。
这些u,v怎么取,显然就和矩阵M的方向有关了。OK,让我们换一个思路来看这个矩阵。平面内的一个矩阵乘以一个向量v,大概简单的写成Mv,它会使得这个向量发生一个作用:旋转,拉伸,平移…总之,这种作用叫做 线性变换,矩阵的左边好像也是一个向量,只不过是横着写的([u v]),换而言之,那就是 vT(v的转置)。
vT(Mv)…这是啥?
意思好像是。。。。v先旋转+拉伸一下,然后再在它自己身上投影,最终的 E(u,v)本质上来说,就是这个投影的长度。。。嗯,对,投影的长度
好了。我们现在明确了 E(u,v) 的数学几何意义,再回过头来想想,要怎样才能让这个投影的长度达到最大或者最小呢?
显然,答案就是矩阵的特征值与特征向量,当[u v]T 取特征向量方向的时候,矩阵M只有拉伸作用,而没有旋转作用,这时的投影长度是最长的(如果反向投则是负的最长)。
好了。我们现在明确了 E(u,v) 的数学几何意义,再回过头来想想,要怎样才能让这个投影的长度达到最大或者最小呢? 显然,答案就是矩阵的特征值与特征向量,当[u v]T 取特征向量方向的时候,矩阵M只有拉伸作用,而没有旋转作用,这时的投影长度是最长的(如果反向投则是负的最长)。
1.两个特征值都很大==========>角点(两个响应方向)
2.一个特征值很大,一个很小=====>边缘(只有一个响应方向)
3.两个特征值都小============>平原地区(响应都很微弱)
基于上述特征,有很多人设计了角点的快速判据。
有 det(M) - trace(M)^2
有 det(M)/trace(M)
…等等很多,但是这不重要,思想都是一样的。(某师姐这里又有一个标定算法的创新点哦。。。。我会告诉你换换判据又是个新思路?)
3. 3DHarris
在2DHarris里,我们使用了 图像梯度构成的 协方差矩阵。 图像梯度。。。嗯。。。。每个像素点都有一个梯度,在一阶信息量的情况下描述了两个相邻像素的关系。显然这个思想可以轻易的移植到点云上来。
OOPS,糟糕,点云木有灰度的概念啊,一般的点云也木有强度的概念啊。。。这可如何是好??????
别紧张,pcl 说这样能行,那就肯定能行咯,先定性的分析一下Harris3D的理念。
想象一下,如果在 点云中存在一点p
1、在p上建立一个局部坐标系:z方向是法线方向,x,y方向和z垂直。
2、在p上建立一个小正方体,不要太大,大概像材料力学分析应力那种就行 3、假设点云的密度是相同的,点云是一层蒙皮,不是实心的。
a、如果小正方体沿z方向移动,那小正方体里的点云数量应该不变
b、如果小正方体位于边缘上,则沿边缘移动,点云数量几乎不变,沿垂直边缘方向移动,点云数量改变
c、如果小正方体位于角点上,则有两个方向都会大幅改变点云数量
OK,我们已经有了Harris3D的基本准则,接下来要思考的是怎样优雅的解决这个问题, 两个和z相互垂直的方向。。。。嗯。。。。perpendicular。。。。
如果由法向量x,y,z构成协方差矩阵,那么它应该是一个对称矩阵。而且特征向量有一个方向是法线方向,另外两个方向和法线垂直。
那么直接用协方差矩阵替换掉图像里的M矩阵,就得到了点云的Harris算法。
其中,半径r可以用来控制角点的规模
r小,则对应的角点越尖锐(对噪声更敏感)
r大,则可能在平缓的区域也检测出角点
r怎么取? 我也不知道。。。。。试吧。。。。。
4.PCL对Harris算法的实现
根据以上分析,在PCL的API文档的帮助下,我尝试了一下 Harris3D 算法。感谢山大的毕同学提供的点云,该点云是场景点云而不是一般的物体点云。总体感觉是慢,因为针对每个点云,需要计算它的法线,算完之后又要针对每个点进行协方差矩阵的计算,总而言之,整个过程还是非常耗时的。并且说实话。。。算法的效果一般般。
#include 
由于我选择的搜索半径比较大,所以找到的角点都不是太"角”,关于参数设置大家可以多多探索,但我认为,特征点检测算法实在太慢,对实时机器人系统来说是远远达不到要求的。这种先算法线,再算协方差的形式真心上不起。。。。实际上这种基于领域法线的特征点检测算法有点类似基于 CRF的语义识别算法,都只使用了相邻信息而忽略了全局信息。也可能相邻信息包含的相关性比较大,是通往高层次感知的唯一路径吧,谁又知道呢?
PCL—关键点检测(iss&Trajkovic)
关键点检测往往需要和特征提取联合在一起,关键点检测的一个重要性质就是旋转不变性,也就是说,物体旋转后还能够检测出对应的关键点。不过说实话我觉的这个要求对机器人视觉来说是比较鸡肋的。因为机器人采集到的三维点云并不是一个完整的物体,没哪个相机有透视功能。机器人采集到的点云也只是一层薄薄的蒙皮。所谓的特征点又往往在变化剧烈的曲面区域,那么从不同的视角来看,变化剧烈的曲面区域很难提取到同样的关键点。想象一下一个人的面部,正面的时候鼻尖可以作为关键点,但是侧面的时候呢?会有一部分面部在阴影中,模型和之前可能就完全不一样了。
也就是说现在这些关键点检测算法针对场景中较远的物体,也就是物体旋转带来的影响被距离减弱的情况下,是好用的。一旦距离近了,旋转往往造成捕获的仅有模型的侧面,关键点检测算法就有可能失效。
1. ISS算法
ISS算法的全程是Intrinsic Shape Signatures,第一个词叫做内部,这个词挺有讲究。说内部,那必然要有个范围,具体是什么东西的范围还暂定。如果说要描述一个点周围的局部特征,而且这个物体在全局坐标下还可能移动,那么有一个好方法就是在这个点周围建立一个局部坐标。只要保证这个局部坐标系也随着物体旋转就好。
方法1.基于协方差矩阵
协方差矩阵的思想其实很简单,实际上它是一种耦合,把两个步骤耦合在了一起
1.协方差矩阵的思想其实很简单,实际上它是一种耦合,把两个步骤耦合在了一起
2.利用奇异值分解求这些向量的0空间,拟合出一个尽可能垂直的向量,作为法线的估计
协方差矩阵本质是啥?就是奇异值分解中的一个步骤。。。。奇异值分解是需要矩阵乘以自身的转置从而得到对称矩阵的。
当然,用协方差计算的好处是可以给不同距离的点附上不同的权重。
方法2.基于齐次坐标
1.把点的坐标转为齐次坐标
2.对其次坐标进行奇异值分解
3.最小奇异值对应的向量就是拟合平面的方程
4.方程的系数就是法线的方向。
显然,这种方法更加简单粗暴,省去了权重的概念,但是换来了运算速度,不需要反复做减法。其实本来也不需要反复做减法,做一个点之间向量的检索表就好。。。
但是我要声明PCL的实现是利用反复减法的。
方法2.基于齐次坐标
1.把点的坐标转为齐次坐标
2.对其次坐标进行奇异值分解
3.最小奇异值对应的向量就是拟合平面的方程
4.方程的系数就是法线的方向。
显然,这种方法更加简单粗暴,省去了权重的概念,但是换来了运算速度,不需要反复做减法。其实本来也不需要反复做减法,做一个点之间向量的检索表就好。。。
但是我要声明PCL的实现是利用反复减法的。
ISS特征点检测的思想也甚是简单:
1.利用方法1建立模型
2.其利用特征值之间关系来形容该点的特征程度。
显然这种情况下的特征值是有几何意义的,特征值的大小实际上是椭球轴的长度。椭球的的形态则是对邻近点分布状态的抽象总结。试想,如果临近点沿某个方向分布致密则该方向会作为椭球的第一主方向,稀疏的方向则是第二主方向,法线方向当然是极度稀疏(只有一层),那么则作为第三主方向。
如果某个点恰好处于角点,则第一主特征值,第二主特征值,第三主特征值大小相差不会太大。
如果点云沿着某方向致密,而垂直方向系数则有可能是边界。
总而言之,这种局部坐标系建模分析的方法是基于特征值分析的特征点提取。
最后补充,Intrisic指的就是这个椭球的内部。
pcl::PointCloud<pcl::PointXYZRGBA>::Ptr model (new
pcl::PointCloud<pcl::PointXYZRGBA> ());;
pcl::PointCloud<pcl::PointXYZRGBA>::Ptr model_keypoints (new
pcl::PointCloud<pcl::PointXYZRGBA> ());
pcl::search::KdTree<pcl::PointXYZRGBA>::Ptr tree (new
pcl::search::KdTree<pcl::PointXYZRGBA> ());
// Fill in the model clouddouble model_resolution;
// Compute model_resolution
pcl::ISSKeypoint3D<pcl::PointXYZRGBA, pcl::PointXYZRGBA> iss_detector;iss_detector.setSearchMethod (tree);
iss_detector.setSalientRadius (6 * model_resolution);
iss_detector.setNonMaxRadius (4 * model_resolution);
iss_detector.setThreshold21 (0.975);
iss_detector.setThreshold32 (0.975);
iss_detector.setMinNeighbors (5);
iss_detector.setNumberOfThreads (4);
iss_detector.setInputCloud (model);
iss_detector.compute (*model_keypoints);2. Trajkovic关键点检测算法
角点的一个重要特征就是法线方向和周围的点存在不同,而本算法的思想就是和相邻点的法线方向进行对比,判定法线方向差异的阈值,最终决定某点是否是角点。并且需要注意的是,本方法所针对的点云应该只是有序点云。
本方法的优点是快,缺点是对噪声敏感。


