Java数据结构和算法之归并排序(详细图解)
归并排序介绍:
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
归并排序思想示意图1-基本思想:
归并排序思想示意图2-合并相邻有序子序列:
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤
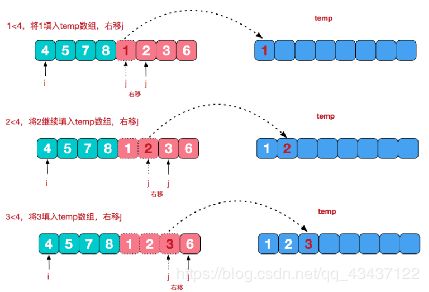

代码如下:
package com.guigu.sort;
import java.util.Arrays;
public class MergeSortDemo {
public static void main(String[] args) {
int[] arr = {20,45,46,13,78};
int[] temp = new int[arr.length]; //辅助数组
mergeSort(arr, 0, arr.length - 1, temp);
System.out.println(Arrays.toString(arr));
}
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid, temp);
mergeSort(arr, mid + 1, right, temp);
merge(arr, left, mid, right, temp);
}
}
//合并的方法
/**
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int t = 0; // 指向temp数组的当前索引
int j = left; // 初始化j, 左边有序序列的初始索引
int k = mid + 1; //初始化k, 右边有序序列的初始索引
// (一)
// 先把左右两边(有序)的数据按照规则填充到temp数组
// 直到左右两边的有序序列,有一边处理完毕为止
while(j <= mid && k <= right) {
//如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素
//即将左边的当前元素,填充到 temp数组
//然后 t++, j++
if(arr[j] <= arr[k]) {
temp[t] = arr[j];
j += 1;
t += 1;
}else { // 反之,将右边有序序列的当前元素,填充到temp数组
temp[t] = arr[k];
k += 1;
t += 1;
}
}
//(二)
//把有剩余数据的一边的数据依次全部填充到temp
while(j <= mid) { //左边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[j];
j += 1;
t += 1;
}
while(k <= right) { //右边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[k];
k += 1;
t += 1;
}
//(三)
// 将temp数组的元素拷贝到arr
// 注意,并不是每次都拷贝所有
t = 0;
int cur = left;
// 第一次合并 tempLeft = 0 , right = 1 // tempLeft = 2 right = 3 // tL=0 ri=3
// 最后一次 tempLeft = 0 right = 7
while(cur <= right) {
arr[cur] = temp[t];
cur += 1;
t += 1;
}
}
}
运行结果:
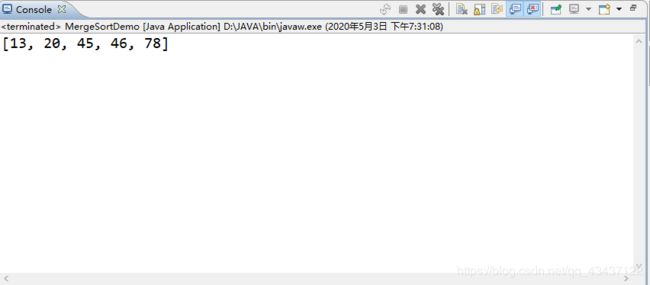
总结: 归并排序运用的是分治思想,这个典型算法能充分体现分治的思想。这个题的难点在于合并时,首先你要对两个数组进行合并,然后再看那个先合并完了或者同时合并完了。接着就是最后的数组拷贝,你每次合并时 left 和 right 的范围是变得,而每次temp里面的元素个数刚好是right - left + 1 (也就是遍历时从left 遍历到 right),这个地方可以好好理解下。
