对数group卷积,一种比普通group卷积更实用的卷积
前言
目前在很多移动端的设备当中,对深度模型的要求是低功耗与低内存,低功耗意味着计算量小,低内存意味着参数量少,以一个[H,W,C]图片经过[C,k,k,Cout]为例:
计算量为HWCkkCout(不算bais)
参数量:CkkCout
可以看出计算量以及参数量受多方面的限制
而目前解决这种问题的两个主流发方法:
(1)深度分离卷积(MobileNet)
(2)Group卷积(AlexNet,ResNeXt)
这里深度分离卷积我们先不表
主要说一下group卷积
例如group=4
这时候变为了四个[C/4,k,k,Cout/4]的卷积
参数量与计算量变为了原先的1/4
但是普通的group比较粗暴,这时候引入了Logarithmic Filter Groups来解决一些问题。
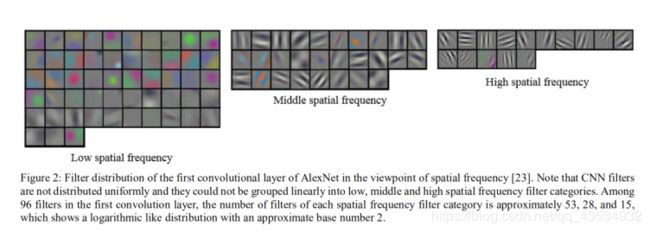
这篇文章发现在channel数为96的这一层卷积中,低通filter,中通,以及高通成2倍的关系,所以说采用对数组卷积7是由一定意义的。
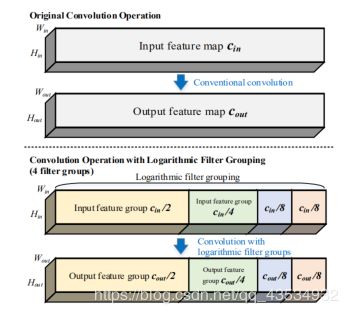
其结构如图所示
代码实现
import tensorflow as tf
length=50#帧长
input=39#MFCC特征维数
def Logarithmic_Filter_Groups(x,kernel_size,outchannel):
split0,split1=tf.split(x ,2 ,2)
outchannel1=outchannel/2
print(split0,split1)
split0=tf.layers.conv1d(split0,outchannel1,kernel_size,strides=1, padding='same')
split1_0,split1_1=tf.split(split1 ,2 ,2)
outchannel2=outchannel1/2
print(split1_0,split1_1)
split1_0=tf.layers.conv1d(split1_0,outchannel2,kernel_size,strides=1, padding='same')
split1_1_0,split1_1_1=tf.split(split1_1 ,2 ,2)
outchannel3=outchannel2/2
print(split1_1_0,split1_1_1)
split1_1_0=tf.layers.conv1d(split1_1_0,outchannel3,kernel_size,strides=1, padding='same')
split1_1_1=tf.layers.conv1d(split1_1_1,outchannel3,kernel_size,strides=1, padding='same')
output=tf.concat( [split0, split1_0, split1_1_0, split1_1_1],-1)
return output
x = tf.placeholder(tf.float32,[None,length,input])#输入数据
conv1=tf.layers.conv1d(x,40,3,strides=1, padding='same')#第一层TDNN
log_layer1=Logarithmic_Filter_Groups(conv1,9,40)
## **输出结果**
```python
Tensor("split:0", shape=(?, 50, 20), dtype=float32) Tensor("split:1", shape=(?, 50, 20), dtype=float32)
Tensor("split_1:0", shape=(?, 50, 10), dtype=float32) Tensor("split_1:1", shape=(?, 50, 10), dtype=float32)
Tensor("split_2:0", shape=(?, 50, 5), dtype=float32) Tensor("split_2:1", shape=(?, 50, 5), dtype=float32)