机器学习线性回归——正规方程求解点的拟合直线

正规方程
设一个线性回归问题中有m条训练数据S={($x$⁽¹⁾,y⁽¹⁾),($x$⁽²⁾,y⁽²⁾)，…($x$^(m),y^(m))}
其中每一个x⁽ⁱ⁾均为n维向量，且首位为1.定义$X$与$y$为如下矩阵：

可见，$X$是一个mn矩阵，$y$是一个m1列向量，$X$称为特征矩阵，$y$称为标签向量，基于这个定义，线性回归算法的目标函数等价于

$mi{n}_{w\in R^n}F(w)=||Xw-y|{|}^2$（1）

在式（1）的目标函数中，$w$为$n\times 1$列向量，$Xw$为矩阵乘积。由于$X$是一个$m\times n$的矩阵，所以$Xw$是一个$m\times 1$列向量。因而，$Xw-y$也是一个$m\times 1$列向量。目标函数$F(w)$为该列向量的L₂范数平方。

设$X^{T}X$为可逆矩阵，则式(1)有唯一最优解$w^{\ast }=(X^{T}X)$^-1$X^{T}y$
由于$\nabla$$F(w)=2X^{T}Xw-2X^{T}y$,所以$w\ast$为最优解当且仅当$w^{\ast }$满足如下方程：$2X^{T}Xw-2X^{T}y=0$
此方程也称为正规方程，$X^{T}X$可逆时，该方程有唯一解$w^{\ast }=2X^{T}Xw-2X^{T}y=0$。

正规方程算法实现：

import numpy as np

def fit(X, y):  #训练模型
    w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)  # w*=(XT⦁X)-1⦁X⦁y
    return w#利用上式计算最优解，并保存在w中

def predict(X,y):  # 预测X对应的Y值
    w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
    return X.dot(w)  # Y_pred = X ⦁ w*

def mean_squared_error(y_true, y_pred):  # 计算均方误差
    return np.average((y_true - y_pred) ** 2, axis=0)

def r2_score(y_true, y_pred):  # 计算决定系数
    numerator = (y_true - y_pred) ** 2
    denominator = (y_true - np.average(y_true, axis=0)) ** 2
    return 1 - numerator.sum(axis=0) / denominator.sum(axis=0)

def generate_samples(m):  #生成服从特征与标签的分布采样  
    X = 2*(np.random.rand(m,1)-0.5)
    y = X + np.random.normal(0,0.3,(m,1))
    return X,y

def process_features(X):#处理特征
    m,n = X.shape
    X = np.c_[np.ones((m,1)),X]
    return X

np.random.seed(0)#随机种子
X_train,y_train = generate_samples(100)#生成100条训练数据
X_train = process_features(X_train)
X_test,y_test = generate_samples(100)#生成100条测试数据
X_test = process_features(X_test)


fit(X_train,y_train)
y_pred = predict(X_test,y_test)
mse = mean_squared_error(y_test,y_pred)
r2 = r2_score(y_test,y_pred)
print("mse={} and r2={}".format(mse,r2))
plt.figure()
plt.title("Scatter Fitting")
plt.plot(X_test, y_test, "bs", ms=3)  # 画散点
plt.plot(X_test, y_pred, color='red')  # 打印直线
plt.show()

结果：

mse=[0.08881471] and r2=[0.78107994]

实例操作：
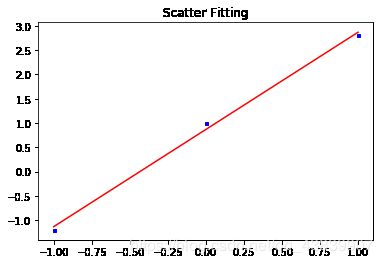
假设有平面上有3个点: (-1.0,-1.2)、(0.0,1.0) 和 (1.0,2.8)。请描述相应的正规方程,并通过求解正规方程来计算关于这3个点的最佳直线拟合。

import numpy as np
import matplotlib.pyplot as plt

def process_features(X):
    m, n = X.shape  # 求X矩阵的行数和列数
    X = np.c_[np.ones((m, 1)), X]  # 将m行1列的矩阵与X拼接
    return X

def fit(X, y):  # 求正规方程
    w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)  # w*=(XT⦁X)-1⦁X⦁y
    return w

def predict(X,y):  # 预测X对应的Y值
    w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
    return X.dot(w)  # Y_pred = X ⦁ w*

def mean_squared_error(y_true, y_pred):  # 求均方误差
    return np.average((y_true - y_pred) ** 2, axis=0)

def r2_score(y_true, y_pred):  # 求决定系数
    numerator = (y_true - y_pred) ** 2
    denominator = (y_true - np.average(y_true, axis=0)) ** 2
    return 1 - numerator.sum(axis=0) / denominator.sum(axis=0)

dots = np.array([[-1.0, -1.2],
                 [0.0, 1.0],
                 [1.0, 2.8]])  # 点坐标
X = dots[:, [0]]  # 取出每个坐标X轴的值
Y = dots[:, [1]]  # 取出每个坐标Y轴的值
X_1 = process_features(X)  # 首位置1

theta = fit(X_1, Y)  # 求解正规方程
Y_pred = predict(X_1,Y)  # 求解X的预测值
mse = mean_squared_error(Y, Y_pred)  # 求均方误差
r2 = r2_score(Y, Y_pred)  # 求决定系数
print("theta:{}".format(theta))
print("mse = {}".format(mse))
print("r2 = {}".format(r2))
plt.figure()
plt.title("Scatter Fitting")
plt.plot(X, Y, "bs", ms=3)  # 画散点
plt.plot(X, Y_pred, color='red')  # 打印直线
plt.show()

结果：

theta:[[0.86666667]
 [2.        ]]
mse = [0.00888889]
r2 = [0.99667774]