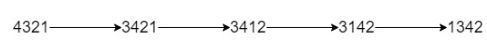leetcode第196场周赛题目及题解

leetcode第196场周赛题目及题解

第一题 leetcode1502 判断能否成为等差数列

题目简介

给你一个数字数组 arr 。如果一个数列中，任意相邻两项的差总等于同一个常数，那么这个数列就称为 等差数列 。
如果可以重新排列数组形成等差数列，请返回 true ；否则，返回 false 。

示例1

输入：arr = [3,5,1]
输出：true
解释：对数组重新排序得到 [1,3,5] 或者 [5,3,1] ，任意相邻两项的差分别为 2 或 -2 ，可以形成等差数列。

示例2

输入：arr = [1,2,4]
输出：false
解释：无法通过重新排序得到等差数列。

数据范围

2 <= arr.length <= 1000；
-10^6 <= arr[i] <= 10^6；

题目分析

这题我们可以利用等差数列的性质，对原数组进行排序，依次判断相邻两项的差与前一个相邻两项的差是否相等，如果相等即为等差数列，否则不能构  
成等差数列。时间复杂度O(nlogn)。

代码展示

class Solution {
public:
    bool canMakeArithmeticProgression(vector<int>& arr) {
        sort(arr.begin(),arr.end());
        for(int i=2;i<arr.size();i++)
        {
            if(arr[i]-arr[i-1]!=arr[i-1]-arr[i-2]) return false;
        }
        return true;
    }
};

第二题 leetcode1503 所有蚂蚁掉下来前的一刻

题目简介

有一块木板，长度为 n 个 单位 。一些蚂蚁在木板上移动，每只蚂蚁都以每秒一个单位的速度移动。其中，一部分蚂蚁向左移动，其他蚂蚁向右移动。
当两只向不同方向移动的蚂蚁在某个点相遇时，它们会同时改变移动方向并继续移动。假设更改方向不会花费任何额外时间。
而当蚂蚁在某一时刻 t 到达木板的一端时，它立即从木板上掉下来。
给你一个整数 n 和两个整数数组 left 以及 right 。两个数组分别标识向左或者向右移动的蚂蚁在 t = 0 时的位置。请你返回最后一只蚂蚁从木板上掉下来的时刻。

示例1

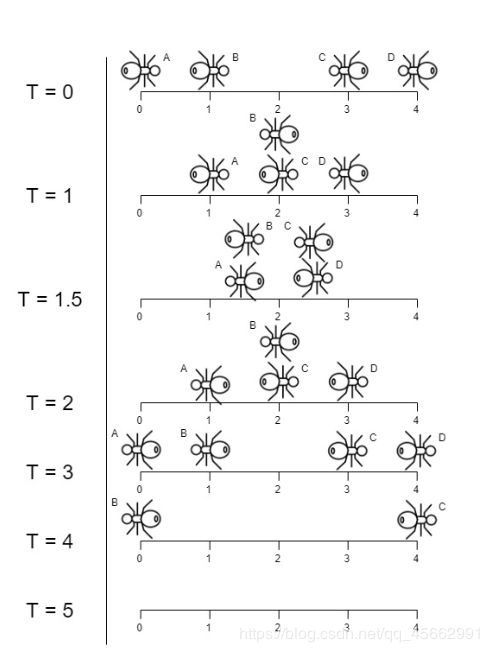
输入：n = 4, left = [4,3], right = [0,1]
输出：4
解释：如上图所示：
-下标 0 处的蚂蚁命名为 A 并向右移动。
-下标 1 处的蚂蚁命名为 B 并向右移动。
-下标 3 处的蚂蚁命名为 C 并向左移动。
-下标 4 处的蚂蚁命名为 D 并向左移动。
请注意，蚂蚁在木板上的最后时刻是 t = 4 秒，之后蚂蚁立即从木板上掉下来。（也就是说在 t = 4.0000000001 时，木板上没有蚂蚁）。

数据范围

1 <= n <= 10^4
0 <= left.length <= n + 1
0 <= left[i] <= n
0 <= right.length <= n + 1
0 <= right[i] <= n
1 <= left.length + right.length <= n + 1
left 和 right 中的所有值都是唯一的，并且每个值 只能出现在二者之一 中。

题目分析

由于两只蚂蚁相遇后会同时改变方向，并且不花费时间，所以我们可以将两只蚂蚁相遇后同时改变方向看成两只蚂蚁互相穿过了对方，这样我们就可以  
直接通过蚂蚁距离右端或左端的距离进行求解。时间复杂度O(n)。

代码展示

class Solution {
public:
    int getLastMoment(int n, vector<int>& left, vector<int>& right) {
        int res=-1;
        for(auto x:left) res=max(res,x);
        for(auto x:right) res=max(res,n-x);
        return res;
    }
};

第三题 leetcode1504 统计全 1 子矩形

题目简介

给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

示例1

输入：mat = [[1,0,1],
            [1,1,0],
            [1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

数据范围

1 <= rows <= 150
1 <= columns <= 150
0 <= mat[i][j] <= 1

题目分析

本题目要求找到所有的全 1 子矩形，我们可以先预处理一个 f 数组，f[i][j]为以第i行第j个点为终点，往上有几个连续的1。然后我们开始枚举子矩形的右  
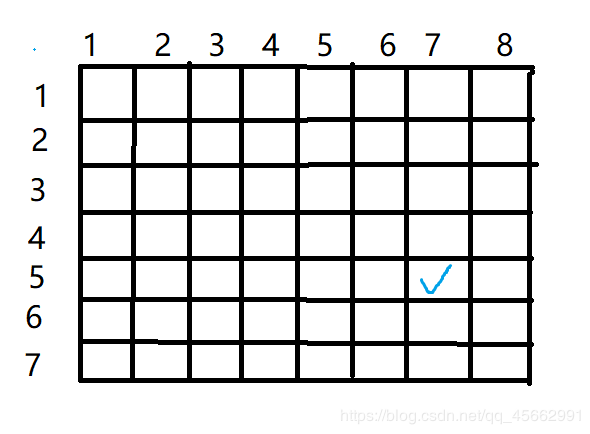
下角端点，之后再枚举子矩形的宽度，每个宽度拥有的子矩形即为这些宽度所对应的f数组的最小值。例如下图，如果我们要找以（5，7）为右下角的  
子矩形有多少个，我们可以先枚举宽度，宽度为1时，个数就是f[5][7];宽度为2时，个数就是min(f[5][7],f[4][7]),以此类推，求出每个宽度有多少个子矩形  
相加即以(5,7)为右下角的子矩形有多少个，这样的时间复杂度为O(n³)；然后我们对此进行优化，我们发现当我们在计算（5，7）这个点时，（5，5），  
（5，6）这些点我们已经处理过了，假设f[5][5]是f[5][7]左边第一个比f[5][7]小的值（这个可以用单调栈来做），并且以（5，5）点为右下角的子矩形有s  
个，那么以（5，7）这个点 为右下角的子矩形的个数就为s+(7-5)*f[5][7];于是我们就将时间复杂度优化到了O(n²)。

代码展示

class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int n=mat.size(),m=mat[0].size();
        vector<vector<int>> f(n,vector<int>(m));
        for(int i=0;i<n;i++) //用递推的方法处理f数组
            for(int j=0;j<m;j++)
                if(mat[i][j])
                {
                    f[i][j]=1;
                    if(i) f[i][j]+=f[i-1][j];
                }
        int res=0;
        for(int i=0;i<n;i++)
        {
            stack<pair<int,int>> stk; //每行开一个新的栈，第一个存列号，第二个存个数
            for(int j=0;j<m;j++)
            {
                int s=0;
                while(stk.size()&&f[i][stk.top().first]>=f[i][j]) stk.pop();
                if(stk.size())
                {
                    s+=stk.top().second;
                    s+=(j-stk.top().first)*f[i][j];
                }
                else
                {
                    s=(j+1)*f[i][j];
                }
                stk.push({j,s});
                res+=s;
            }
        }
        return res;
    }
};

第四题 leetcode1505 最多k次交换相邻数位后得到的最小整数

题目描述

给你一个字符串 num 和一个整数 k 。其中，num 表示一个很大的整数，字符串中的每个字符依次对应整数上的各个 数位 。
你可以交换这个整数相邻数位的数字 最多 k 次。
请你返回你能得到的最小整数，并以字符串形式返回。

示例1

输入：num = "4321", k = 4
输出："1342"
解释：4321 通过 4 次交换相邻数位得到最小整数的步骤如上图所示。

数据范围

1 <= num.length <= 30000
num 只包含 数字 且不含有 前导 0 。
1 <= k <= 10^9

题目分析

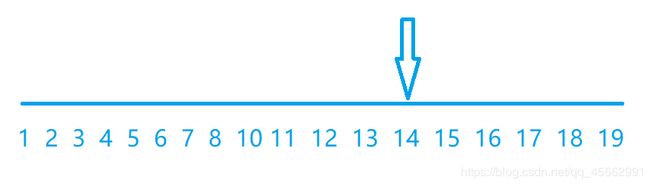
这道题目用贪心的思想去分析，也就是每次都把当前还没有用的最小的数放在前面，那么这样就能保证得到的结果是最小的。例如下图，如果我们需要  
将第14个数移到第一个数上，需要进行14-1=13次交换，并且1-13位置上的数都要相对于原来的位置向后移一位，也就是说1-13中的每一个数都要向右  
偏移一个单位，这些数下次再往前交换时的真实位置就是这些数在原数组中的位置加上偏移的位置；因为偏移的位置需要进行区间修改和单点查询，于  
是我们可以用树状数组和差分来进行记录。时间复杂度O(nlogn)。

代码展示

class Solution {
public:
    int n;
    vector<int> tr;
    int lowbit(int x)
    {
       return x&-x;
    }
    void add(int u,int x)
    {
        for(int i=u;i<=n;i+=lowbit(i)) tr[i]+=x; 
    }
    int get_sum(int x)
    {
        int res=0;
        for(int i=x;i;i-=lowbit(i)) res+=tr[i];
        return res;
    }
    string minInteger(string num, int k) {
        string res="";
        n=num.size();
        queue<int> q[10];
        string nums=' '+num;
        tr.resize(n+1);
        for(int i=1;i<=n;i++) q[nums[i]-'0'].push(i);//把字符串中的数记录到相应的队列中，记录的值为该数在原数组中的位置
        for(int i=1;i<=n;i++)
            for(int j=0;j<10;j++)
            {
                if(q[j].size())
                {
                    int t=q[j].front();
                    int pos=t+get_sum(t); //计算原位置加上偏移量
                    if(pos-i<=k)
                    {
                        k-=pos-i;
                        q[j].pop();
                        res+=to_string(j);
                        add(1,1),add(t,-1); //记录偏移量
                        break;
                    }
                }
            }
            return res;
    }
};

本篇文章题目简介部分均引自leetcode网站。