有趣的高速缓存实验——Cache Lab

任务A

---

注意事项

1. 我们要编写的是一个模拟器，并不是真正的cache，目的是要有像csim-ref的如下的功能。
   
2. 我们的替换策略为LRU，即“最近最少使用”策略。
3. 我们在程序完成进行测试时，需要使用使用提供的< tracefile >，其内容的含义为
   

即I操作与命中不命中无关
L操作会导致命中 / 未命中 / 未命中+LRU替换
S操作会导致命中 / 未命中 / 未命中+LRU替换
M操作(即一次L+一次S)会导致命中+命中 / 未命中+命中 / 未命中+LRU替换+命中

4. 提示中可使用getopt函数来读取命令中参数
   

---

可能遇到的问题

运行csim-ref 和 test-csim、driver.py出现permission denied

这是因为你对文件的读写权限不够
可在vscode终端中执行 chmod 777 ./file_name 的命令升级权限

使用getopt函数中optarg指针时报错

需要在函数前声明 extern char* optarg

---

开始编程

首先明确我们大体需要的功能

1. 构造cache的数据结构
2. 读取命令行中参数的函数
3. 按命令中参数对cache数据结构初始化的函数
4. 解析 tracefile 文件中内容的函数
5. 实现LRU的函数
6. 实现修改cache中数据的函数
7. 判断是否命中
8. 实现L,S,M操作并对hits，misses，evictions进行修改的函数

---

给出我的一些宏定义和全局变量

#define MAX_LRU 999
extern char *optarg;
int hits,misses,evictions; 
hits=misses=evictions=0;
    int s,E,b;
    int detail=0//看要不要因为V而打印详细过程;

---

构造cache的数据结构

这是cache的一般模型，根据此，我们可以构造cache的数据结构。

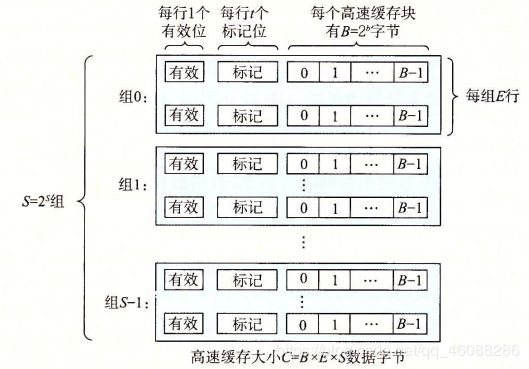
因为我们需要执行LRU的执行政策，所以每个块（行）都需要有一个LRU字段以及tag位和valid位
组就是行的一个数组
cache是组的一个数组，且cache也包括了一些规格参数，S和E，以确定数组大小

typedef struct//首先构造行的数据结构
{
    int valid;
    int tag;
    int lru;//因为我们需要执行LRU的执行政策，所以每个块（行都需要有一个LRU字段）
}cache_line;

typedef struct
{
    cache_line* lines;  //组就是行的一个数组

}cache_set;

typedef struct 
{
    cache_set* set;
    int E;
    int S;//cache是组的一个数组，且cache也包括了一些规格参数，S和E，以确定数组大小
}cache_im;

---

读取命令行中参数的函数

可以看到csim-ref中有一个打印帮助表的，所以我们先来实现一个打印表
很简单，就复制粘贴。

void print_help_list()
{
   printf("Usage: ./csim-ref [-hv] -s  -E  -b  -t \n");
   printf("Options:\n");
   printf("  -h         Print this help message.\n");
   printf("  -v         Optional verbose flag.\n");
   printf("  -s    Number of set index bits.\n");
   printf("  -E    Number of lines per set.\n");
   printf("  -b    Number of block offset bits.\n");
   printf("  -t   Trace file.\n\n");
   printf("Examples:\n");
   printf("  linux>  ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n");
   printf("  linux>  ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n");
}

然后开始编写读取命令的函数
detail用来判断是否需要展示细节
s，E，b都代表书上的标准含义

int get_command(int agrc,char** agrv,int* s,int* E, int* b,int* detail,char* file_name)
{
     int op;
    while((op=getopt(agrc,agrv,"hvs:E:b:t:"))!=-1){
        switch(op){
            case 'h': print_help_list();break;
            case 'v': *detail=1;break;     //用来判断是否需要展示细节
            case 's': *s = atoi(optarg);break;
            case 'E': *E = atoi(optarg);break;
            case 'b': *b = atoi(optarg);break;//s，E，b都代表书上的标准含义
            case 't': strcpy(file_name,optarg);break;
            default : printf("input error\n");break;
        }
    }
    return 0;
}

---

按命令中参数对cache数据结构初始化的函数

根据读入的s，E，b，我们可以得到
共有2^s 组，每组E个块，每块有2^b字节
所以可以得出S,E的值；并且可以确定数组大小使用malloc来开辟空间
并将 valid和 lru初始化为0

int ini_cache(int s,int E,int b,cache_im* mycache)
{
    if(s<0)
    {
        printf("wrong sets numbers!\n");
        exit(0);
    }
    mycache->S=2<<s;
    mycache->E=E;
    mycache->set=(cache_set* )malloc(mycache->S*sizeof(cache_set));
    if(!mycache->set)
    {
        printf("Sets malloc storage wrong!\n");
        exit(0);
    }
    for(int i=0;i<mycache->S;i++)
    {
        mycache->set[i].lines=(cache_line* )malloc(E*sizeof(cache_line));
        if(!mycache->set)
        {
        printf("lines malloc storage wrong!\n");
        exit(0);
        }
        for(int j=0;j<E;j++)
        {
            mycache->set[i].lines[j].valid=0;
            mycache->set[i].lines[j].lru=0;
        }
    }
    return 1;
}

---

解析 tracefile 文件中内容的函数

经过前面几步，我们的准备工作就做好了，接下来是要开始准备对 tracefile 进行操作
第一步，解析地址

写出分别获得组索引和标记位的函数

int get_set_number(int address,int s,int b)
{
    address=address>>b;
    int mask=(1<<s)-1;
    return address&mask;
}

int get_tag_number(int address,int s,int b)
{
    int mask=s+b;
    return address>>mask;
}

---

实现LRU和未命中时对cache中更新数据的函数

既然我们现在可以得到操作的地址，那么我们在进行L,S,M之前就要先把轮子造好。
即先实现我们需要的其他功能，最后集成到L,S,M操作中去

首先进行LRU的实现
我们采取给每个使用的块赋值 MAX_LRU （宏定义）,同时给其他块的 lru–的操作来实现LRU

void up_lru(cache_im* mycache,int set_bit,int hit_index)
{
    mycache->set[set_bit].lines[hit_index].lru=MAX_LRU;
    for(int i=0;i<mycache->E;i++)
    {
        if(i!=hit_index)
        {
            mycache->set[set_bit].lines[i].lru--;
        }
    }
}

下面是寻找最小LRU的函数

int find_LRU(cache_im* mycache,int set_bit)
{
    int min_index=0;
    int min_lru=MAX_LRU;
    for(int i=0;i<mycache->E;i++)
    {
        if(mycache->set[set_bit].lines[i].lru<min_lru)
        {
            min_index=i;
            min_lru=mycache->set[set_bit].lines[i].lru;
        }
    }
    return min_index;
}

因此，在未命中进行更新cache时
如果未满，则不需要LRU替换，只需要更新每个块的LRU即可
如果满了，则进行LRU替换策略即把牺牲快的tag改为地址中的tag，并对每个块的LRU进行更新
该函数也会返回是否满的状态

int up_cache(cache_im* mycache,int set_bit,int tag_bit)
{
    int full=1;
    int i;
    for(i=0;i<mycache->E;i++)
    {
        if(mycache->set[set_bit].lines[i].valid==0)
        {
            full=0;
            break;
        }
    }
    if(!full)
    {
        mycache->set[set_bit].lines[i].valid=1;
        mycache->set[set_bit].lines[i].tag=tag_bit;
        up_lru(mycache,set_bit,i);
    }
    else
    {
        int scarfice=find_LRU(mycache,set_bit);
        mycache->set[set_bit].lines[scarfice].valid=1;
        mycache->set[set_bit].lines[scarfice].tag=tag_bit;
        up_lru(mycache,set_bit,scarfice);
    }
    return full;   
}

---

实现判断是否命中的函数

这个很简单了，就根据组索引遍历，看是否得到 tag位相同且valid==1的块，如果有则命中
否则未命中

int judge_miss(cache_im* mycache,int set_bit,int tag_bit)
{
    int miss=1;
    for(int i=0;i<mycache->E;i++)
    {
        if(mycache->set[set_bit].lines[i].valid==1&&mycache->set[set_bit].lines[i].tag==tag_bit)
        {
            miss=0;
            up_lru(mycache,set_bit,i);
        }
    }
    return miss;
}

---

实现L,S,M操作

最后我们只需要实现L,S,M即可。
前面已经实现了判断是否命中的函数。
命中时，只需要对hits++；
未命中时up_cache（更新cache的块）和可能要执行的LRU策略都已经实现
轮子都造好了，我们只需要拼装就可以了

如果未命中没有满，则misses++
如果未命中且满，则evictions++
命中则hits++
另外，我们还要注意detail的值，即用户是否输入了 -v选项
若输入，则要把hits、misses、evictions三种情况之一打印出来

void load_data(cache_im* mycache,int address,int size,int set_bit,int tag_bit,int detail)
{
    if(judge_miss(mycache,set_bit,tag_bit)==1)
    {
        misses++;//如果未命中没有满，则misses++
        if(detail)
        printf("miss");
        if(up_cache(mycache,set_bit,tag_bit)==1)//如果未命中且满，则evictions++
        {
            evictions++;
            if(detail)
            printf("evictions");
        }
    }
    else
    {
        hits++;//命中则hits++
        if(detail)
        printf("hit");
    }
}

开始我们就分析过了，S操作和L操作对hits，misses，evictions影响相同，直接调用即可。
M操作是先执行了L,后执行了M，分别调用即可。

void store_data(cache_im* mycache,int address,int size,int set_bit,int tag_bit,int detail)
{
    load_data(mycache,address,size,set_bit,tag_bit,detail);
}
void modify_data(cache_im* mycache,int address,int size,int set_bit,int tag_bit,int detail)
{
    load_data(mycache,address,size,set_bit,tag_bit,detail);
    store_data(mycache,address,size,set_bit,tag_bit,detail);
}

---

最后的main函数

说了这么久的准备工作，我们还需要从tracefile中读取数据
应该也是很简单的，对前面实现的函数进行组合即可

int hits,misses,evictions; 

int main(int agrc,char* agrv[])
{
    hits=misses=evictions=0;
    int s,E,b;
    int detail=0;
    char file_name[100];
    char op[10];
    cache_im mycache;
    get_command(agrc,agrv,&s,&E,&b,&detail,file_name);
    ini_cache(s,E,b,&mycache);
    FILE *trace_file=fopen(file_name,"r");
    int address,size;
    while(fscanf(trace_file,"%s %x,%d",op,&address,&size)!=EOF)
    {
        if(strcmp(op,"I")==0)
        continue;
        int tag_bit=get_tag_number(address,s,b);
        int set_bit=get_set_number(address,s,b);
        if(detail)
        {
            printf("%s,%x,%d",op,address,size);
        }       
        if(strcmp(op,"L")==0)
        {
            load_data(&mycache,address,size,set_bit,tag_bit,detail);
        }
        if(strcmp(op,"S")==0)
        {
            store_data(&mycache,address,size,set_bit,tag_bit,detail);
        }
        if(strcmp(op,"M")==0)
        {
            modify_data(&mycache,address,size,set_bit,tag_bit,detail);
        }
        if(detail)
            printf("\n");
    }
    printSummary(hits,misses,evictions);
    return 0;
}

OKK，那么任务A就暂告完成了！！！
这是我的打分界面

---

任务B

优化矩阵转置运算程序。在trans.c中编写一个矩阵转置函数，尽可能的减少程序对高速缓存访问的未命中次数。
评分方式

任务A只是考验了我们的编程能力，实验B才是真正的考验思维啊QWQ

首先对一个4X4引例进行分析

我们的cache规格为 s=5，E=1，b=5
即共有32组，每组一个块、每块有32字节的空间（即可存放8个int型数据）
地址的后5位为块偏移，中间5位为组索引，剩余位为标记位

我们首先使用一个4X4的二维数组来看下trans.c中提供给我们的转置函数对内存访问情况

./test-trans -M 4 -N 4

然后生成了一个trace.f1文档，里面是一个内存追踪文件
然后我们使用任务A的csim函数对内存访问进行追踪

./csim -v -s 5 -E 1 -b 5 -t trace.f1

生成了如下条目，分割线下面是对数组的存取

数组的前8个元素存在一个组，后8个元素存在另一个组

S 38b08c,1 miss 
L 38b0c0,8 miss 
L 38b084,4 hit 
L 38b080,4 hit 
-----------------------------------------------//下面是对数组进行的L,S操作
L 30b080,4 miss eviction //110000101100 00100 00000  读A[0][0]，冲突未命中
S 34b080,4 miss eviction //111000101100 00100 00000  写B[0][0]，冲突未命中
L 30b084,4 miss eviction //110000101100 00100 00100  读A[0][1]，冲突未命中
S 34b090,4 miss eviction //110100101100 00100 10000  写B[1][0]，冲突未命中
L 30b088,4 miss eviction //110000101100 00100 01000  读A[2][0]，冲突未命中
S 34b0a0,4 miss          //110100101100 00101 00000  写B[2][0]，
                         //已经到了后8个元素可以看到组索引换了，冷未命中。
L 30b08c,4 hit 
S 34b0b0,4 hit 
L 30b090,4 hit 
S 34b084,4 miss eviction 
L 30b094,4 miss eviction 
S 34b094,4 miss eviction 
L 30b098,4 miss eviction 
S 34b0a4,4 hit 
L 30b09c,4 hit 
S 34b0b4,4 hit 
L 30b0a0,4 miss eviction 
S 34b088,4 miss eviction 
L 30b0a4,4 hit 
S 34b098,4 hit 
L 30b0a8,4 hit 
S 34b0a8,4 miss eviction 
L 30b0ac,4 miss eviction 
S 34b0b8,4 miss eviction 
L 30b0b0,4 miss eviction 
S 34b08c,4 hit 
L 30b0b4,4 hit 
S 34b09c,4 hit 
L 30b0b8,4 hit 
S 34b0ac,4 miss eviction 
L 30b0bc,4 miss eviction 
S 34b0bc,4 miss eviction 
S 38b08d,1 miss eviction 
hits:15 misses:22 evictions:19

举部分例子
L 30b080,4 miss eviction //110000101100 00100 00000 读A[0][0]，冲突未命中
S 34b080,4 miss eviction //111000101100 00100 00000 写B[0][0]，冲突未命中
L 30b084,4 miss eviction //110000101100 00100 00100 读A[0][1]，冲突未命中
S 34b090,4 miss eviction //110100101100 00100 10000 写B[1][0]，冲突未命中
L 30b088,4 miss eviction //110000101100 00100 01000 读A[2][0]，冲突未命中
S 34b0a0,4 miss //110100101100 00101 00000 写B[2][0]，
//已经到了后8个元素可以看到组索引换了，冷未命中。

---

后面的元素可以依次这样推出
我们看到，L、S成对出现了共16次
即冲突未命中占22次misses的绝大部分，因此我们的目的就是解决冲突未命中
而冲突未命中原因是A和B中下标相同的元素会映射到同一块内存
所以下面我们要处理的就是这个问题

---

case：M32 N32

先使用提供的转置函数test一下

我滴妈呀，1183次misses是我妹想到的
因为32X32的矩阵中一行32个元素已经超出了一个块最多能存的8个int型
现在使用普通转置算法时，必定有很多元素没有缓存
因此，我们应该采取分块技术来保证每个操作单元都能被完全缓存到内存中
最优的选择是按8分块
来进行编写

for(int i=0;i<M;i+=8)
{
    for(int j=0;j<N;j+=8)
    {
        for(int ii=i;ii<i+8;ii++)
        {
            for(int jj=j;jj<j+8;jj++)
            B[jj][ii]=A[ii][jj];
        }
    }
}

可以看到变成了343，有了大幅度进步，但还达不到300以下的要求
继续分析，可以知道因为对角线元素进行转置时
仍然会造成冲突未命中，因此我们需要对对角线元素进行操作

有一个想法就是空间换时间
即在第一次缓存A中元素时，直接取出这一个块的全部元素
然后直接对B中对应的转置位置的元素进行修改

 for(i=0;i<M;i+=8)
        {
            for(j=0;j<N;j+=8)
            {
                for(ii=i;ii<i+8;ii++)
                {
                    temp1=A[ii][j];
                    temp2=A[ii][j+1];
                    temp3=A[ii][j+2];
                    temp4=A[ii][j+3];
                    temp5=A[ii][j+4];
                    temp6=A[ii][j+5];
                    temp7=A[ii][j+6];
                    temp8=A[ii][j+7];
                    B[j][ii]=temp1;
                    B[j+1][ii]=temp2;
                    B[j+2][ii]=temp3;
                    B[j+3][ii]=temp4;
                    B[j+4][ii]=temp5;
                    B[j+5][ii]=temp6;
                    B[j+6][ii]=temp7;
                    B[j+7][ii]=temp8;
                }
            }
        }

可以看到结果已经达到了287次，已经满分了
由于时间原因当时没有深究，但现在我发现这个程序还有改进的地方

在上面的程序中我们可以看到
A数组的每个块只会造成一次未命中，已经最优了
但B数组的访问除了一次冷未命中外，对角线元素还会造成冲突未命中，这点很致命
这就是造成我们的程序没有达到最优的256次misses的原因
感兴趣的读者可以先自己去探索一下
等我写完实验报告再回来填坑QWQ

case：M 64 N 64

我们先看看延续上一次按8分块的思想，能否有效地降低misses

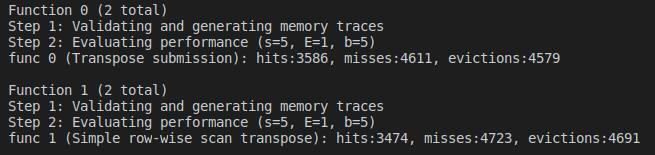
4611:4723 很不理想啊

我们来分析一下为什么行不通
因为矩阵每行需要8个块才能缓存完
因此高速缓存只能缓存4行的矩阵
因此如果我们采用8X8的分块技术，那么后四行就会因为没有被缓存而造成冲突未命中
所以我们尝试一下使用4X4的分块技术，应该会有很大的改观

for(i=0;i<M;i+=4)
        {
            for(j=0;j<N;j+=4)
            {
                for(ii=i;ii<i+4;ii++)
                {
                    temp1=A[ii][j];
                    temp2=A[ii][j+1];
                    temp3=A[ii][j+2];
                    temp4=A[ii][j+3];
                    B[j][ii]=temp1;
                    B[j+1][ii]=temp2;
                    B[j+2][ii]=temp3;
                    B[j+3][ii]=temp4;
                }
            }
        }

果然有了显著的提升，但还是达不到想要的效果
分析得知
一个块的大小是8个 int型，可我们现在只用了4个，并没有充分利用我们加载好的缓存
对于A来说，每次的缓存都会被充分利用（根据上述代码可得）
现在主要看对B的访问
对B的访问顺序为
前4行前4列->后4行前4列->前4行后4列->后4行后4列。
即前四行前四列访问完后还有每个块4个int缓存
但对后四行前四列的访问会覆盖掉前四行前四列的块
因此在后面的两次访存中均会有两次未命中

---

所以我们要做的就是充分利用B的缓存
我们来一步步分析
假设我们是要把右上角的8X8矩阵（A）转置到左下角(B)
1.步骤一
按照上面的分析
将右上区域的前4行全部存入左下区域的前4行，这个过程右上区域前4行的前4列已经转置完成，但是对于前4行的后4列还没有放入应该放的位置，但是为了不再访问同一个块，我们同时将数据取出，存入还没有用到的区域中。
直接使用A中缓存一步搞定
变成了这个样子

2. 步骤二
然后我们再对A进行逐列的进行后4行前四列的转置，其过程如下所示：
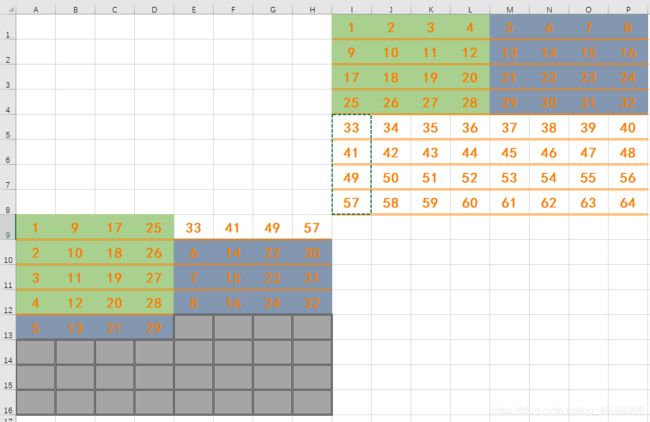逐列逐列进行
最后变成这个亚子
3.步骤三
最后我们再对后四行后四列进行转置

---

我们来分析一下这个过程中B的未命中情况
步骤一： B数组缓存前四行（前四行各有一次冷未命中）
步骤二： B数组逐行访问前四行后四列（无未命中），后四行前四列（冷未命中）
步骤三： B数组逐行访问后四行后四列（无未命中）
可以看到我们实现了将之前的每行两次未命中缩减为每行一次未命中
下面是我们的实例函数

for(i=0;i<N;i+=8)
        {
			for(j=0;j<M;j+=8){
				for(ii=i;ii<i+4;ii++){
					temp1=A[ii][j];
                    temp2=A[ii][j+1];
                    temp3=A[ii][j+2];
                    temp4=A[ii][j+3];
					temp5=A[ii][j+4];
                    temp6=A[ii][j+5];
                    temp7=A[ii][j+6];
                    temp8=A[ii][j+7];

					B[j][ii]=temp1;
                    B[j+1][ii]=temp2;
                    B[j+2][ii]=temp3;
                    B[j+3][ii]=temp4;
					B[j][ii+4]=temp5;
                    B[j+1][ii+4]=temp6;
                    B[j+2][ii+4]=temp7;
                    B[j+3][ii+4]=temp8;
				}
				for(jj=j;jj<j+4;jj++){
					temp1=A[i+4][jj];
                    temp2=A[i+5][jj];
                    temp3=A[i+6][jj];
                    temp4=A[i+7][jj];
					temp5=B[jj][i+4];
                    temp6=B[jj][i+5];
                    temp7=B[jj][i+6];
                    temp8=B[jj][i+7];

					B[jj][i+4]=temp1;
                    B[jj][i+5]=temp2;
                    B[jj][i+6]=temp3;
                    B[jj][i+7]=temp4;
					B[jj+4][i]=temp5;
                    B[jj+4][i+1]=temp6;
                    B[jj+4][i+2]=temp7;
                    B[jj+4][i+3]=temp8;
				}
				for(ii=i+4;ii<i+8;ii++){
					temp1=A[ii][j+4];
                    temp2=A[ii][j+5];
                    temp3=A[ii][j+6];
                    temp4=A[ii][j+7];
					B[j+4][ii]=temp1;
                    B[j+5][ii]=temp2;
                    B[j+6][ii]=temp3;
                    B[j+7][ii]=temp4;
				}
			}
		}

1179次，满分咯！

case： M 61 N 67

乍一看这个矩阵很难处理的亚子
但毛主席说过“一切反动派都是纸老虎”，所以我们不要怕（doge）
由于这个很特殊，分成4X4 8X8的块的话就会导致每行分离，很难计算
所以我们索性分为16X16的矩阵块

for(i=0;i<N;i+=16)
        {
            for(j=0;j<M;j+=16)
            {
                for(ii=i;ii<i+16&&ii<N;ii++)
                {
                    for(jj=j;jj<M&&jj<j+16;jj++)
                    {
                        B[jj][ii]=A[ii][jj];
                    }
                }
            }
        }

哦，我的天啊，这么好的运气简直就和隔壁露西姑妈烤的蓝莓派一样可口。
前人积攒了数千年的运气都集中到我身上了呢，奔涌吧！转置！
就不详细分析了，太欧了…