数学(1)初一上学期数学笔记
初一上学期数学笔记
1.正数
正数是数学术语,比0大的数叫正数(positive number),0本身不算正数。正数与负数表示意义相反的量。
正数前面常有一个符号“+”,通常可以省略不写。
2.负数
负数是数学术语,比0小的数叫做负数,负数与正数表示意义相反的量。
负数用负号(Minus Sign,即相当于减号)“-”和一个正数标记
3.非负数
正数与零的统称
4.非正数
负数与零的统称
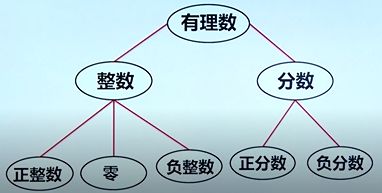
5.有理数
6.数轴
在数学中,可以用一条直线上的点表示数,这条直线 叫做数轴(number line),它满足以下要求:
(1)在直线上任取一个点表示0这个点叫做原点(origin);
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1(向右1个单位长度),2(向右2个单位长度),3(向右3个单位长度),…;从原点向左,用类似方法依次表示-1(向左1个单位长度),-2(向左2个单位长度),-3(向左3个单位长度)…
7.相反数:
如果两个数的和为0,那么这两个数互为相反数。
只有符号不同的两个数叫做互为相反数,其中的一个数叫做另一个数的相反数。
(a≠0)a的相反数是-a,0的相反数是0。
8.绝对值:
在数轴上表示一个数的点离原点的距离就叫做这个数的绝对值
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数。0的绝对值是0。
公式|a|=?
若a大于0, 则a的绝对值还等于a;
若a等于0 ,则a的绝对值等于0 ;
若a小于0, 则a的绝对值等于a 。
9.有理数的加法
符号相同的两个数相加,结果的符号不变,只是两个绝对值相加。
(-5)+(-3)= -8
符号相反的两个数相加,结果的符号与绝对值较大的加数符号相同,并用较大的绝对值减去较小的绝对值。
(-3)+(5)= 5
法则:
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,绝对值相等时,和为零;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值;
一个数同零相加仍得这个数。
有理数的加法交换律和结合律
1)把正数和负数分别结合在一起相加
2)把互为相反数的结合,能凑整的结合
3)把同分母的结合相加
10.有理数的减法
有理数减法法则:减去一个数,等于加上这个数的相反数。
用公式表示为: a-b=a+(-b)
11.有理数的乘法
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何和零相乘,都得0
如何进行两个有理数得相乘运算
先确定积得符号,再把绝对值相乘,当一个因数为0时,积为0
乘法交换律:两个数相乘,交换因数的位置,积相等
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等
乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,在吧积相加
12.有理数的除法
有理数除法法则:
除以一个数等于乘以这个数的倒数
用公式表示为: a/b=a*(1/b) (b!=0)
两个数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不等于0得数,都得0。
有理数得加减乘除运算顺序
先算乘除,后算加减,有括号的要先算括号里的
13.有理数得乘方
乘方的意义,表示n个相同的数相乘,比如n个a相乘, 求n个相同因数的积得运算叫做乘方

乘方负数得奇次幂是负数,乘方负数得偶次幂时正数。
乘方正数得任何次幂都是正数,0得任何正整数次幂都是0。
1得任何次幂都是1
科学计数法
乘方可以用来简化大数字写法作用,同时也便于记忆。
例如:
70000人口。
科学计数法:7 * 10⁴
可以把一个大于10的数表示a*10 ⁿ,其中a大于或等于1小于10,n为正整数。使用的是科学计数法。
近似数
准确数是与实际完全符合的数
近似数是与实际非常接近的数,差别不回很大
误差 = 近似值 - 准确值
14.有理数加、减、乘、除、乘方混合运算顺序:
1.先算乘方,在乘除,最后加减。
2.同级运算,从左到右进行。
3.如果有括号,先算括号内的运算,按小括号、中括号、大括号依次进行。
15.整式
整式为单项式和多项式的统称,是有理式的一部分,在有理式中可以包含加,减,乘,除、乘方五种运算,但在整式中除数不能含有字母。
由数或字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式。
在含有字母的式子中,若出现乘号,通常将乘号写作“.”或者省略不写,100*a可以写成100.a或100a
都是数或字母的积,像这样的式子叫做单项式,单独的一个数或一个字母也是单项式
比如6a a² 2.5x 52%m km²
单项式中,所有数字因数叫做这个单项书的系数
单项式中,所有字母的指数的和叫做这个单项式的次数
例如:
6a² 的系数是6,次数是2
a³ 的系数是1,次数是3
16.单项式注意
1)单独一个数字或者字母也叫单项式
2)单独一个非零数的次数是0
3)单项式的系数包括符号,当系数为1或-1时,这个1可省略不写
4)分母含有字母的式子不属于单项式。
5)单项式是字母与数的乘积。
17.多项式
几个单项式的和叫做多项式
单项式与多项式统称整式
18.整式分类
19.同类项
所含的字母相同,并且相同的字母的指数也相同,那么就是同类型
常数也是同类项
合并同类项法则
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
20.多项式去括号法则
1)如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同
2)如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反
21.整式加减的运算法则
一般情况,几个整式相加减,如果有括号,先去括号,然后在合并同类项。
22.从算式到方程
含有未知数的等式叫做方程
一元一次方程的定义:只含有一个未知数(元)未知数的次数都是1,这样的方程叫做一元一次方程。
一元一次方程满足的条件:
1)一个未知数。
2)未知数的次数是1。
3)未知数的系数不为0。
23.检验一个数值是不是方程的解的步骤
1)将数值代入方程左边进行计算,
2)将数值代入方程右边进行计算,
3)比较左右两边的值,若左边等于右边,则是方式的解,反之,则不是。
24.等式的性质
1.等式两边同时(加减)同一个数或式子结果仍然相等。
2.等式两边同时乘以同一个个数或同时除于同一个不为0的数,结果仍相等。
利用这些性质可以求解一元一次方程。
25.一元一次方程解方程
一般步骤:
1.去分母
2.去括号
3.移项
4.合并同类项
5.系数化为1
需要注意:
1.移项时要改变符号
2.合并同类项时,知识吧同类项的系数相加,作为所得项的系数,字母部分不变。
3.系数化为1,也就是说方程两边同时除以未知数前面的系数。
4.去分母时,应在方程的左右两边乘以分母的最小公倍数。
5.去分母的依据的等式性质二,去分母时不能漏乘没有分母的项。
6.去分母与去括号这两步分开写,不要跳步,防止忘记变括号。
26.销售的盈亏
27.几何
几何图形都是由点、线、面、体、组成的。点是构成所有图形的基本元素。
点无大小,线有直线和曲线,面有平的面和曲的面。
点动成线,线动成面,面动成体。
体是由面围成,面与面相交成线,线与线相交成点。
28.直线、线段、射线
直线:直线是两端都没有端点、可以向两端无限延伸、不可测量长度的。当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点。
线段:直线上两个点和他们之间的部分叫做线段,这两个点叫线段的端点。
射线:直线上的一点和它一旁的部分叫射线,这个点叫射线的端点。
当
比较两条线段长短方法:
1.观察。
2.度量方法。
3.重叠比较两个角。
29.角
角是由具有公共端点的两条射线组成的图形,这两条射线叫做角的边,它们的公共端点叫做角的顶点。
平角与周角:角也可以看作是一条射线绕着它的端点旋转而形成的图形。一条射线绕它的端点旋转,当终边与始边在一条直线时,所成的角叫做平角。终边继续旋转,当它和始边重合时,所称的角叫周角。
角的表示方法:
用三个大写英文字母表示,例:∠AOC(顶点写在中间)
用一个大写英文字母表示,例:∠O
用数字表示,例:∠1
用1个希腊字母表示,例:∠β
角度度数:
1周角=2平角=4直角=360度
1平角=180度
1直角=90度
1度=60分
1分=60秒
锐角(acute angle):大于0°,小于90°的角叫做锐角。 [3]
直角(right angle):等于90°的角叫做直角。
钝角(obtuse angle):大于90°而小于180°的角叫做钝角。
平角(straight angle):等于180°的角叫做平角。
优角(major angle):大于180°小于360°叫优角。
劣角(minor angle):大于0°小于180°叫做劣角,锐角、直角、钝角都是劣角。
周角(round angle):等于360°的角叫做周角。
负角(negative angle):按照顺时针方向旋转而成的角叫做负角。
正角(positive angle):逆时针旋转的角为正角。
零角(zero angle):等于0°的角。
比较两个角大小的方法:
1.观察
2.重合比较
3.使用工具度量方法比较
角的平分线
从一个角的顶点引出一条射线,把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线。
补角:两个角的和等于180度(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个角的补角。
余角:两个角的和等于90度(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角。