FPGA视觉从入门到放弃——稀疏编码的原理与简单应用

先试一下它的效果。根据MNIST公开的分类器 1，误分类率小于0.6%的与卷积网络相关的方法主要有两种：2008年的“无监督稀疏特征 + 支持向量机”和起始于1998年的“卷积网络”。两者的特征提取分别基于稀疏编码和卷积神经网络。

1. 问题

不同的尺度和视角拍摄同1个正方体。FPGA中物体检测采用滑动窗口也能跑得飞起，所以问题来了~

• 滑动窗口尺寸多尺度，能否识别不同视角的正方体？
• 滑动窗口尺寸不变，能否识别不同尺度和视角的正方体？

2. 原理

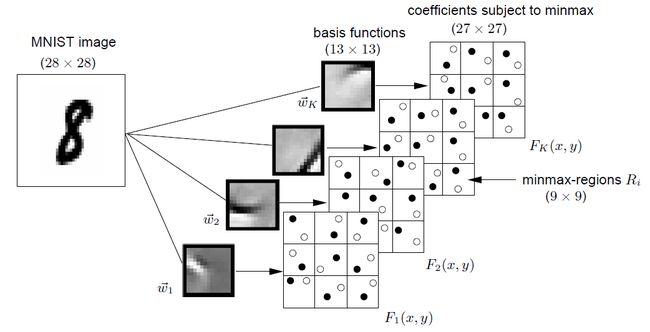
系数图像 Fj 包括输入图像块的基函数 ωj→ 的系数 aj 。

自编码网络只有1个隐含层，输入层到隐含层用于编码，隐含层到输出层用于解码。网络训练的目标为对编码后的输入解码的结果尽可能逼近原来的输入。

F⃗ (x,y)=(F1(x,y),F2(x,y),...,FK(x,y))=argmina⃗ (||∑j=1Kω⃗ jaj−P(x,y)||+βS(a⃗ ))

其中， K 为隐含层节点个数(不包括偏置项)， ω⃗  为隐含层到输出层的连接权重， a⃗  为隐含层输出， P(x,y) 为在输入图像坐标系中的中心位置为 (x,y) 的块去中心化的像素值， S(a⃗ ) 为令隐含层节点输出稀疏的正则项， F⃗ (x,y) 为目标函数最小时，输入图像的每个图像块的隐含层的线性激活函数的输出。

有实验证明视觉皮层中复杂细胞的行为可以通过局部极大操作描述，并且人类会用同样的规则考虑位置的不确定性 2。

最后的特征向量变为：

fI=(Fmax1(R1),...,FmaxK(R1),...,Fmax1(RM2),...,FmaxK(RM2)))

其中， M2 为1幅图像的块个数， F1 ~ FK 分别为第 1−K 个隐含层节点的输出， Fmax 和 Fmin 分别为每个隐含层节点的极大和极小值。

Fmaxj(Ri)=maxx,y∈RiFj(x,y)Fminj(Ri)=minx,y∈RiFj(x,y)

这里， (x,y) 是属于非重叠的图像块 Ri 的像素点，但并不一定是图像块 Ri 的中心像素点。不过原文在计算图像块的均值时，定义 (x,y) 为中心位置的像素坐标。

该方法提取特征的流程如下：

• 稀疏编码获得能够表示数字0~9的基函数(文中提到“每个基函数由 13×13 个像素组成，为简化，基函数个数等于每个基函数的像素数(169)”)；
• 对图像中每个像素点用基函数“滤波”，每个基函数对应1幅 27×27 的激活输出图像；
• 每个激活输出图像分成9个区域，计算每个区域的极大极小值，并排列成行向量。

解决空间相关性时，有个问题可以考虑：
a) 原文的方法符合生物视觉皮层的单细胞模型属性。虽然前面的特征提取方法只是与稀疏编码的基函数的组合，但猫的电极实验得到的模型却是激活输出后的局部极大操作；
b) 局部感受野提取原图像的特征时有空间相关性。所以，整个图像按像素滤波一定可以保留足够多的特征，但这些特征冗余得有点多。

那么，多放1个空间相关性在激活输出的前面会怎么样？ (￣ε(#￣) 无非是冗余的特征变少，测试错误率往下轻微一跌。原文这么做只是更有力地证明了局部极大操作对特征输出的贡献。

3. 简单应用

前面的问题和思路可用来做些不太靠谱的小实验。对于小数据，没必要那么有深度~

原图为用FPGA板的Sobel算子得到的边缘图像。

(1) 整体

a. 尺度

对于单尺度，裁剪得到正方体图像，图像大小缩放至 32×32 (如左1)；
对于多尺度，用 120×120 大小的滑动窗口在原图像中扫描，整个滑动窗口的图像大小缩放到 32×32 (如左2)。

b. 稀疏编码

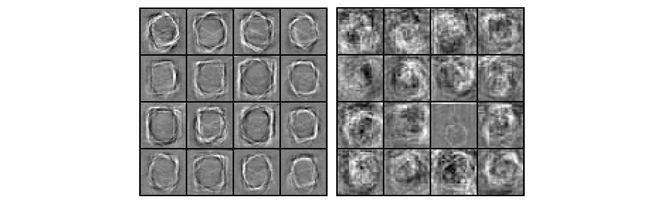
从单尺度和多尺度的正样本缩放图像中随机采样图像块。稀疏编码后得到基函数 (左1为单尺度，左2为多尺度)：

单尺度下感觉圆或者多边形都有可能误检测，多尺度下根本没什么效果。

c. 分类

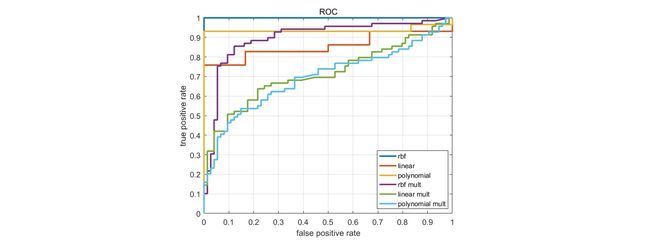
稀疏编码后的输出按0.7:0.3比例分成训练和测试部分，送进不同核函数的支持向量机。多尺度的效果明显不行，单尺度的特征向量最好二次稀疏编码，否则支持向量比例过高。总体感觉整个模型是过拟合的。

(2) 局部

a. 尺度

对于单尺度，裁剪得到正方体图像，图像大小缩放至 32×32 (如左1和左2)；
对于多尺度，用 120×120 大小的滑动窗口在原图像中扫描，整个滑动窗口的图像大小缩放到 32×32 (如左3和左4)。

b. 结构

对于无结构，对缩放后的图像随机采样100个归一化的图像块(每个图像块的大小为 8×8 ，如左1和左3)；
对于带结构，对缩放后的图像按空间顺序采集16个归一化的图像块(如左2和左4)。

归一化时，全黑图像块得到的方差为0，所以给方差加上1个很小的数。

带结构的单尺度背景图像如下：

c. 极大极小

对每个图像块所有的隐含层输出求极大极小值。与前面原理部分不同的是，前面每个隐含层节点都有自己的极大极小值。如果无结构，则计算随机位置处的隐含层节点的极大极小值；如果带结构，则计算每个非重叠空间位置处的所有隐含层节点的极大极小值。

这样的计算会产生一种潜在假设：所有空间位置对全局物体的影响权重相同。但这个权重在后面的二分类时却有体现。所以，管它呢~

d. 稀疏编码

从单尺度和多尺度的正样本缩放图像中随机采样图像块(属于半监督学习)，每个图像采样100个归一化的正样本图像块。稀疏编码后得到基函数 (左1为单尺度，左2为多尺度)：

e. 分类

分类时，随机把特征输出按0.6:0.4的比例分成训练数据和测试数据。Holdout交叉验证(分离比例为0.6)得到线性核的支持向量机。

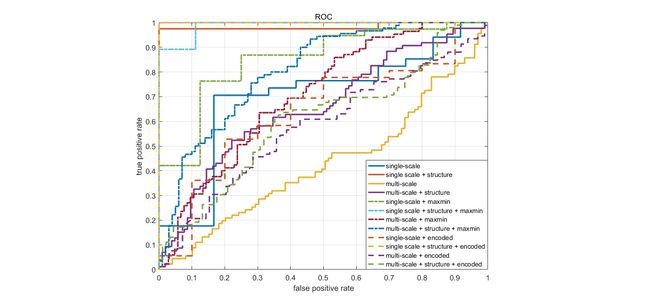
别人家的ROC曲线好平滑的样子，我的却是这样…

• 单尺度效果总是比多尺度好；
• 结构对单尺度改善很多，多尺度改善一点点且不能用；
• 极大极小对单尺度和多尺度都有改善，但依然不可用；
• 二次稀疏编码使得单尺度且带结构的效果更加满意，但未提高单尺度且不带结构的效果，对多尺度的效果不会改进。

胡说八道结束，欢迎拍砖~ (｡・`ω´･)