Kaggle:Getting Started of Titanic
一、概要
泰坦尼克号幸存预测是Kaggle上参与人数最多的的比赛之一,要求参赛人员预测乘客是否能够幸存,是一个典型的二分类问题。
二、数据简介
官网提供训练数据集train.csv和测试数据集test.csv和一个提交样例数据集,数据中的各个字段如下:
PassengerId: 乘客的ID
Survived:1代表幸存,0代表遇难
Pclass:票类别-社会地位, 1代表Upper,2代表Middle,3代表Lower
Name:姓名
Sex:性别
Age:年龄
SibSp:兄弟姐妹及配偶的个数
Parch:父母或子女的个数
Ticket:船票号
Fare:船票价格
Cabin:舱位
Embarked:登船口岸
三、数据探索
1、加载数据
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
path = '/titanic/data/{}'
train = pd.read_csv(path.format('train.csv'))
test = pd.read_csv(path.format('test.csv'))
2、概览
train.info()
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
数据中有大量的数值型数据,这部分可以考虑直接使用;其他非数值型数据要探索一下如何分类;同时里面存在一定量的缺失值,这部分要注意填充或者丢弃。
3、分类样本
train['Survived'].value_counts()
0 549
1 342
样本量很小,同时存在不平衡的问题,可能需要考虑调整。
4、特征权重
train_corr = train.drop('PassengerId', axis=1).corr()
train_corr

计算数值型字段的协方差,可以看到Pclass与Fare和生存的相关性相对比较明显。
5、特征探索
(1)Pclass
随着船票等级的降低,人数逐渐增加,同时生存率也大大下降,相关性很明显,后续模型需要考虑这个特征。
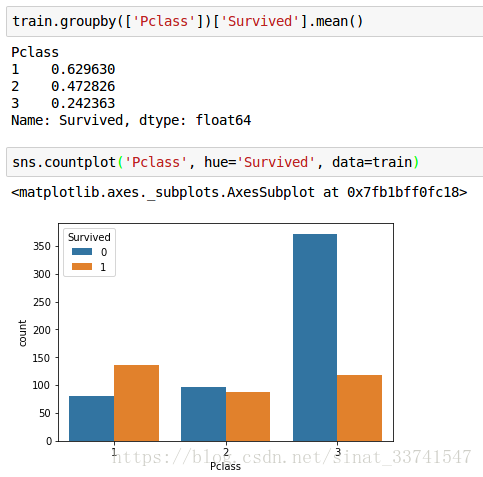
(2)Sex
妇女小孩先走,女性明显有更高的幸存率。
train.groupby('Sex')['Survived'].mean()
Sex
female 0.742038
male 0.188908
Name: Survived, dtype: float64
(3)Age
Age字段缺失数量较多,先去除缺失数据,再整体观察

根据年龄段的不同,生存出现明显左右高,中间低的现象,对年龄进行分组再对比
age_not_miss['Age'] = pd.cut(age_not_miss['Age'], bins=[0, 18, 30, 45, 100], labels=[1,2,3,4])
age_not_miss.groupby('Age')['Survived'].mean()
Age
1 0.503597
2 0.355556
3 0.425743
4 0.368932
未成年人明显具有更高的生存率。
(4)Sibsp + Parch
前面协方差表看到Sibsp和Parch与生存率之间存在一定的关系,但不是特别明显,这里可以考虑将这两个特征组合成一个新特征Family再进行观察
train['F_size'] = train['SibSp'] + train['Parch'] + 1
train.groupby('F_size')['Survived'].mean()
F_size
1 0.303538
2 0.552795
3 0.578431
4 0.724138
5 0.200000
6 0.136364
7 0.333333
8 0.000000
11 0.000000
Name: Survived, dtype: float64
可以看到家庭人数在2-4人的情况下,具有较高的生存率,而单独一个与家庭人数大于等于5人的生存率明显降低
(5)Ticket
船票出现重复的数量比较少,这里可以考虑把船票重复与否派生出另一个特征,因为相同的船票代表可能为相互认识的人,从而在逃生的时候更可能出现聚堆的情况。
(6)Fare
从协方差表能看到Fare与生存率有相对明显的关系,因为船票价格众多,先分组
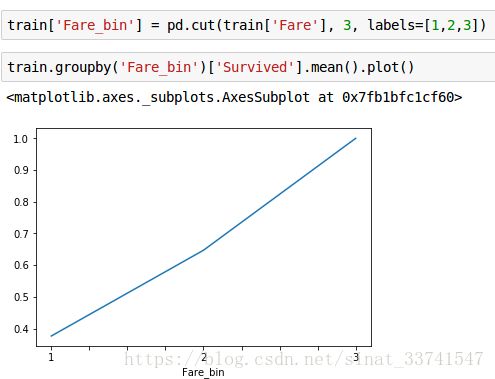
可以看出,很明显的递增关系。
(7)Cabin
舱位缺失数量非常多,可能无法提取出足够的信息,可以考虑以舱位缺失与否及舱位前缀作为特征。
(8)Embarked
登船港口有一个缺失值,可以考虑用众数填充或不做处理,C港上船的乘客明显具有更高的生存率,同一个港口上船更可能分布在船中的同一片区域,从而影响生存率。
train.groupby(['Embarked'])['Survived'].mean()
Embarked
C 0.553571
Q 0.389610
S 0.336957
Name: Survived, dtype: float64
(9)Name
Name中包含了对乘客的称呼、性别及可能的社会地位等信息,这里需要先对信息进行抽取,再结合领域知识进行特征构建,这个放到后边再列出来。
四、特征构建
构建特征时,先把训练集和测试集合并到一起
test['Survived'] = 0
train_test = train.append(test)
1、船票等级
船票等级只需要简单的把数据分列即可,构造one-hot向量
train_test = pd.get_dummies(train_test, columns=['Pclass'], prefix='P')
2、名称
对于名称,先用正则表达式提取出其中的称呼
train_test['Name1'] = train_test['Name'].str.extract('.*?,(.*?)\.').str.strip()
对于称呼进行分类,最终构造出了四类特征
train_test['Name1'].replace(['Master'], 'Master' , inplace = True)
train_test['Name1'].replace(['Jonkheer', 'Don', 'Sir', 'the Countess', 'Dona', 'Lady', 'Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Royalty' , inplace = True)
train_test['Name1'].replace(['Mme', 'Ms', 'Mrs', 'Mlle', 'Miss'], 'Mrs' , inplace = True)
train_test['Name1'].replace(['Mr'], 'Mr' , inplace = True)
看看这几类特征与生存率的相关性如何
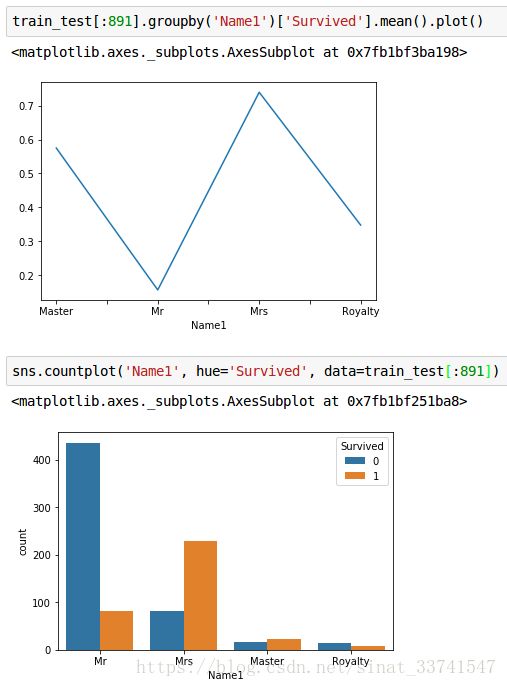
很明显,分组为男士的生存率是最低的,而女士则有占有最高的生存率,Mater组代表了年长同时拥有更高知识水平的人群也获得了极高的存活率,其他剩下的数量较少,但从称号上基本代表了拥有相对高社会身份的人群,如:贵族等。
3、性别
同1,直接分组即可
train_test = pd.get_dummies(train_test, columns=['Sex'], prefix='S')
4、家庭
家庭按照人口数量,分为4个组别
train_test['F_size'] = train_test['SibSp'] + train_test['Parch'] + 1
train_test['F_Single'] = train_test['F_size'].map(lambda s: 1 if s == 1 else 0)
train_test['F_Small'] = train_test['F_size'].map(lambda s: 1 if 2<= s <= 3 else 0)
train_test['F_Med'] = train_test['F_size'].map(lambda s: 1 if s == 4 else 0)
train_test['F_Large'] = train_test['F_size'].map(lambda s: 1 if s >= 5 else 0)
5、船票
按照是否共享船票,提取特征
tpc = train_test['Ticket'].value_counts().reset_index()
tpc.columns = ['Ticket', 'Ticket_sum']
train_test = pd.merge(train_test, tpc, how='left', on='Ticket')
train_test.loc[train_test['Ticket_sum'] == 1, 'T_share'] = 0
train_test.loc[train_test['Ticket_sum'] != 1, 'T_share'] = 1
6、船票价格
船票价格可能和船票等级及登船港口相关,根据这两个特征,找到对应的均值,填充缺失值
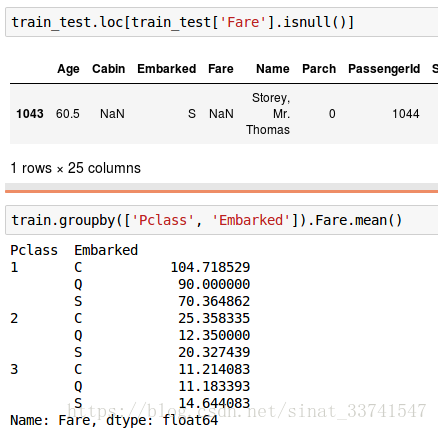
根据Embarked为S,填充之后分组
train_test['Fare'].fillna(14.644083, inplace=True)
train_test['Fare_bin'] = pd.cut(train_test['Fare'], 3, labels=[1,2,3])
7、船舱
根据是否缺失及船舱首字母构造特征
train_test['Cabin'] = train_test['Cabin'].apply(lambda x: str(x)[0] if pd.notnull(x) else x)
train_test.loc[train_test['Cabin'].isnull(), 'Cabin_nan'] = 1
train_test.loc[train_test['Cabin'].notnull(), 'Cabin_nan'] = 0
train_test = pd.get_dummies(train_test, columns=['Cabin'])
8、港口
直接用众数S填充缺失值,分组
train_test['Embarked'].fillna('S')
train_test = pd.get_dummies(train_test, columns=['Embarked'], prefix='E')
9、年龄
先提取年龄是否缺失特,这很有可能与是否生存有关系
train_test.loc[train_test['Age'].isnull(), 'Age_nan'] = 1
train_test.loc[train_test['Age'].notnull(), 'Age_nan'] = 0
后面考虑建立模型填充缺失的年龄数据,剔除可能与年龄无关或者冗余的字段
miss_age = train_test.drop(['PassengerId', 'Name', 'Ticket', 'Fare', 'Survived'], axis=1)
miss_age_train = miss_age[miss_age['Age'].notnull()]
miss_age_test = miss_age[miss_age['Age'].isnull()]
miss_age_train_x = miss_age_train.drop(['Age'], axis=1)
miss_age_train_y = miss_age_train['Age']
miss_age_test_x = miss_age_test.drop(['Age'], axis=1)
特征都是one-hot向量,先标准化处理一下
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(miss_age_train_x)
miss_age_train_x_ss = ss.transform(miss_age_train_x)
miss_age_test_x_ss = ss.transform(miss_age_test_x)
用贝叶斯模型进行进行预测
from sklearn import linear_model
model = linear_model.BayesianRidge()
model.fit(miss_age_train_x_ss, miss_age_train_y)
train_test.loc[train_test['Age'].isnull(), 'Age'] = model.predict(miss_age_test_x_ss)
最后按年龄段进行分组
train_test['Age'] = pd.cut(train_test['Age'], bins=[0, 18, 30, 45, 100], labels=[1, 2, 3, 4])
train_test = pd.get_dummies(train_test, columns=['Age'], prefix='A')
10、去除冗余特征
feature_columns = ['PassengerId', 'Name', 'Ticket', 'Fare', 'SibSp', 'Parch']
train_test = train_test.drop(feature_columns, axis=1)
11、特征评价
画出特征的协方差图

从相关图上看,我们选取的大部分特征彼此之间都没有太大的相关性,这对于建立模型来说是一个好消息,我们希望每一个特征彼此之间无关,能够提供不同的层面的信息,从而更加充分的表达出数据的整体信息。
五、模型构建
1、数据标准化
和上文提到的预测年龄一样,先分割数据集和标准化数据
train_data = train_test[:891]
test_data = train_test[891:]
train_data_x = train_data.drop(['Survived'], axis=1)
train_data_y = train_data['Survived']
test_data_x = test_data.drop(['Survived'], axis=1)
ss1 = StandardScaler()
ss1.fit(train_data_x)
train_data_x_ss = ss1.transform(train_data_x)
test_data_x_ss = ss1.transform(test_data_x)
2、普通模型
模型调参
from sklearn.model_selection import GridSearchCV
params = {name: value}
cv = GridSearchCV(estimator=cls), param_grid=params, scoring='roc_auc', cv=5)
cv.fit(train_data_x_ss, train_data_y)
cv.best_params_
(1)RandomForestClassifier
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=220, min_samples_leaf=3, max_depth=5, min_samples_split=9)
rf.score(train_data_x_ss, train_data_y)
(2)LogisticRegression
lr = LogisticRegression(class_weight='balanced', C=0.01, max_iter=100)
lr.fit(train_data_x_ss, train_data_y)
lr.score(train_data_x_ss, train_data_y)
(3)SVC
from sklearn import svm
svc = svm.SVC(C=10, max_iter=350, probability=True)
svc.fit(train_data_x_ss, train_data_y)
svc.score(train_data_x_ss, train_data_y)
(4)GradientBoostingClassifier
from sklearn.ensemble import GradientBoostingClassifier
gbdt = GradientBoostingClassifier(learning_rate=0.5, n_estimators=120)
gbdt.fit(train_data_x_ss, train_data_y)
gbdt.score(train_data_x_ss, train_data_y)
(5)XGBClassifier
import xgboost as xgb
xg = xgb.XGBClassifier(learning_rate=0.8, n_estimators=100)
xg.fit(train_data_x_ss, train_data_y)
xg.score(train_data_x_ss, train_data_y)
(6)ExtraTreesClassifier
from sklearn.ensemble import ExtraTreesClassifier
et = ExtraTreesClassifier(n_estimators=200)
et.fit(train_data_x_ss, train_data_y)
et.score(train_data_x_ss, train_data_y)
3、融合模型
(1)VotingClassifier
from sklearn.ensemble import VotingClassifier
rf = RandomForestClassifier(n_estimators=220, min_samples_leaf=3, max_depth=5, oob_score=True)
lr = LogisticRegression(class_weight='balanced', C=0.01, max_iter=100)
svc = svm.SVC(C=10, max_iter=350, probability=True)
gbdt = GradientBoostingClassifier(learning_rate=0.5, n_estimators=120)
xg = xgb.XGBClassifier(learning_rate=0.8, n_estimators=100)
et = ExtraTreesClassifier(n_estimators=200)
vot = VotingClassifier(estimators=[('rf', rf), ('lr', lr), ('svc', svc), ('gbdt', gbdt), ('xg', xg), ('et', et)], voting='hard')
vot.fit(train_data_x_ss, train_data_y)
vot.score(train_data_x_ss, train_data_y)
(2)Stacking
两层模型,先处理数据
from sklearn.cross_validation import StratifiedKFold
clfs = [rf, lr, svc, gbdt, xg, et]
X = np.array(train_data_x_ss)
Y = np.array(train_data_y)
X_test = np.array(train_data_x_ss)
Y_test = np.array(train_data_y)
blend作为第二层模型输入
train_blend = np.zeros((X.shape[0], len(clfs)))
test_blend = np.zeros((X_test.shape[0], len(clfs)))
K-flod
skf = list(StratifiedKFold(Y, 5))
依次训练单个模型,再使用模型的预测值构建第二层模型的输入
for i, clf in enumerate(clfs):
test_blend_i = np.zeros((test_blend.shape[0], len(skf)))
for j, (train, test) in enumerate(skf):
clf.fit(X[train], Y[train])
# 每一个模型的预测值,填充到blend的对应位置,k-flod的测试刚好覆盖
# 全部的训练集,填充blend对应的一列
train_blend[test, i] = clf.predict_proba(X[test])[:, 1]
test_blend_i[:, j] = clf.predict_proba(X_test)[:, 1]
# test_blend相比而言会多出k-1份数据,直接取均值即可
test_blend[:, i] = test_blend_i.mean(1)
第二层模型直接使用逻辑回归
clf2 = LogisticRegression(C=10, max_iter=100)
clf2.fit(train_blend, Y)
clf2.score(test_blend, Y_test)
上述模型中,得分最高的是随机森林,达到了0.80382,位于前11%
六、调优
观察姓名字段,在同一艘船上,姓相同的乘客很有可能是同一家人,从而在逃生的时候分布在同一片区域,这里可以考虑增加特征。
提取乘客的姓名,对于只出现1次的姓,不进行考虑,直接命名为small,而其他则进行分组
train_test['Name2_'] = train_test['Name'].apply(lambda x: x.split('.')[1].strip())
names = train_test['Name2_'].value_counts().reset_index()
names.columns = ['Name2_', 'Name2_sum']
train_test = pd.merge(train_test, names, how='left', on='Name2_')
train_test.loc[train_test['Name2_sum'] <= 1, 'Name2'] = 'small'
train_test.loc[train_test['Name2_sum'] > 1, 'Name2'] = train_test['Name2_']
train_test = pd.get_dummies(train_test, columns=['Name2'], prefix='N')
再次进行模型训练,最终得分0.81339,达到前5%
七、结果
最终得分最高的模型为随机森林,得分为0.81339,排名551/11347,位于Top 5%

八、后续
Titanic是一个入门级的项目,关键点在于对这种比赛套路的认识,从数据分析到特征提取,最后建模调参等。
实际中,特征决定了模型的上限的,而好的模型和参数能够无限逼近这个上限,这也是kaggle社区一致的认识。
上述项目如果想再提升,那么就是对特征的再次发掘,或者用大量的存在一定差异的模型进行模型融合,或许能够得到意想不到的结果。
具体代码可以在我github上找到: https://github.com/lpty/kaggle
在写作过程中,参考了以下文章,在此致谢:
https://github.com/apachecn/kaggle/tree/dev/competitions/getting-started/titanic
http://www.jasongj.com/ml/classification/
