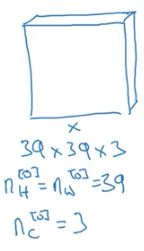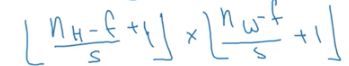【卷积神经网络】Lesson 1--卷积神经网络基础

课程来源：吴恩达 深度学习课程 《卷积神经网络》
笔记整理：王小草
时间：2018年6月4日

---

1.计算机视觉

1.1 计算机视觉的3个问题

（1）图像分类
图像分类是一个在工业界广泛使用的需求，从最早的识别手写数字，邮编到现在的人脸识别。

（2）物体检测
目前物体检测的应用也相当广泛。比如通过城市与道路上的监控视频可以实时捕捉车辆，行人的动态；再比如自动驾驶汽车中也是通过车身上大量摄像头去捕捉周围的环境状况，从而做出相应合理的响应。

（3）风格迁移
这是近几年火了一段时间的风格迁移，虽然在社会价值上还只是娱乐性质，应用在拍照软件上较为多，但是却让人对神经网络的奇妙性大开眼界，相信业界的继续探索还会挖掘更多神奇与好玩的东西。

以上3类问题，在吴恩达的课程中都会一一讲解。

1.2 深度学习在图像上存在的问题

图像有一个很巨大的特点，就是特征为度尤为大。假设一张模糊的像素不高的图片为64*64*3的大小，那么特征就有12288个，假设第一个隐藏层有1000个神经元，那么在全联接下参数的大小为12288*1000，要对图像做分类也好，物体检测也好，一层怎么够，那么于是参数的数目就会急剧增加，从而造成两个缺陷：内存与资源大量消耗+过拟合。
那么于是的于是，就需要我们的“卷积计算”隆重登场了。

2.边缘检测

入门卷积神经网络，先从边缘检测(edge detection)开始了解。

2.1 什么是边缘检测

假设有以下这样一张图，

要让计算机知道图里是什么，首先要进行垂直边缘检测，检测出图像中垂直的部位像这样：

然后要进行水平检测,检测水平的部位，像这样：

2.2 如何进行边缘检测

那么如何进行垂直检测呢，首先来看一个例子：
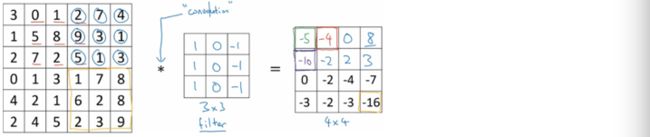
这是一个6*6的灰度图像（即黑白图像，只有一个颜色通道），因此可以表示成6*6*1的矩阵

为了检测图像中的垂直边缘，我们来构造一个3*3的小矩阵，这个东东很多论文里叫”卷积核”(kernel)，吴恩达这边选择叫它”过滤器”(filter).

将图像和这个filter进行卷积计算,得到等号右边的4*4的矩阵
（在数学中表示卷积计算，但在python等代码中表示乘法，注意区分）

来，同学们，我们来做填数字的游戏
首先让filter与图片最左上角的3*3矩阵进行element-wise products：
即3*1+1*1+2*1+0*0+5*0+7*0+1*-1+8*-1+2*-1 = -5，于是等号右边的4*4矩阵的第一行第一列的元素就填上-5.

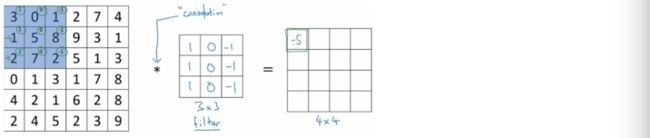
然后将蓝色方形区域在图片上往右移动一格，覆盖住图片上新的3*3矩阵，再进行相似的计算，得到4*4矩阵中第一行第2列的元素为-4

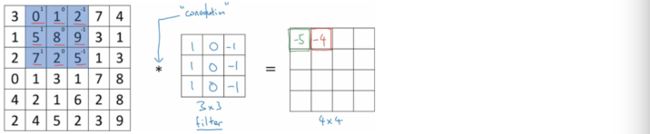
接下来这个小蓝区域会一直继续往右移动，每次只移动一格，直到移动到边界为止，接着会往下移动一格，从左往右继续移动和计算剩下的元素。

直到等号右边的矩阵全部填写完成

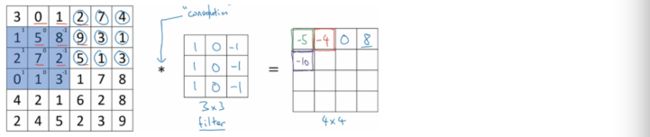
好了，同学们，填数字游戏到此结束，每个人奖励一颗小红花，下课。
额，等等，这就是垂直边缘检测了？哪里垂直了，为什么说这是垂直边缘检测呢？
上面的例子只是为了告诉大家卷积计算的过程，下面来讲一个利用卷积计算，被检测到垂直边缘的例子。

又是一个6*6的图像，数字越大说明越白，数字为0说明是灰色的

表示成图像就像这样，是不是有一个超级明显的垂直边缘呢：

现在，仍然使用一个3*3的filter:

这个filter表示成图像如下，即1位白色，0位灰色，-1为黑色的三个颜色段：

接着让6*6的图像与3*3的filter做卷积计算，得到以下矩阵

神奇的是，进过卷积计算后得到的4*4矩阵，中间两列为30，两边为0，对应的的图像应该是：c

将卷积计算后的图像与原来的图像进行比较，发现原来的垂直线条的地方变成了一块白色区域，也就是说通过计算，我们检测到了原始图像的垂直线条，即计算后的白色线条，当然，这个白色线条有点粗，那是因为原始图像本身太小，放在正常的大图里（比如1000*1000），垂直边缘将被很好得检测出来。

2.3 垂直检测中的明暗过度

上小节中，举了一个垂直边缘检测的例子，如下，原始的图像从左到右是由亮到暗的，于是检测出来的垂直边缘是亮色表示。

那么，现在假设将原始图像变成由暗到亮的过程，如下，则卷积后到输出图像是用暗色来表示垂直边缘的。

也就是说，这个过滤器可以帮助我们区分明暗过度的类型。当然，如果你不介意这两者的区别，那么你可以输出矩阵的绝对值。

2.4 更多边缘检测的例子

也就是说，这个过滤器可以帮助我们区分明暗过度的类型。当然，如果你不介意这两者的区别，那么你可以输出矩阵的绝对值。

注意，3*3的水平边缘过滤器，上方行是亮色，下方行是暗色的。

来个复杂一点的例子，右边原始图像中左上角与右下角为亮色，其他区域为暗色，当它与水平过滤器进行卷积计算后，得到了等号右边的矩阵，可见该矩阵中间两列形成了一条边缘线，由于原图中上下颜色过渡右区别，因此输出矩阵的左边区域是亮色的，而右边区域是暗色的。

总而言之，不同的过滤器可以用于识别垂直与水平的边缘。在文献中，学者们对这两类过滤器也进行了激烈的探讨，比如有学者提出l sobel filter，如下，其优点是给予了中间这一行（处在图像中央的像素点）更多的权重，使得结果的鲁棒性回更高

也有学者更倾向于使用以下过滤器，名叫Scharr filter

在神经网络中，不一定要直接使用学者们提出来的这9个数字，而是可以将过滤器中的数字当作参数，使用梯度下降法与反向传播去学习最有的参数，从而使得图片的边缘能够被很好地检测。学习到的过滤器很可能比学者们手写的过滤器更为有效，它可以检测出45度或者70度等任何角度的边缘。详见之后的章节。

3.卷积

在卷积神经网络中，有以下类别的层次：
（1）convolution卷积层
（2）pooling池化层
（3）fully connected全连接层
本小节讲解卷积层，第4节讲解pooling layer

3.1 padding

为了构建深度卷积神经网络，首先要掌握一个重要的卷积操作，即padding.
回顾前几节中讲到的例子，一个6*6的图像，在与一个3*3的filter进行卷积计算之后，输出一个4*4的矩阵：

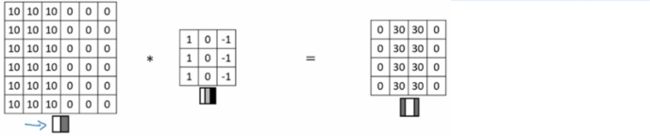
由此我们可以得出，假设图片是n*n，filter是f*f, 那么卷积计算以后的矩阵将是(n-f+1)*(n-f+1)
但是！这样做有两个很显著的缺点：
（1）第一，在实际的应用中，神经网络会设置很多层，若是每次经过卷积之后的得到的矩阵都不断得缩小，不多久我们原来的大图像就会变成很小的图像
（2）第二，经过这样的卷积计算，可见最最角落的像素点将只会被扫过一次，也就是是只会被一个输出所触碰或使用，而中间的像素点，将会被多次触碰与使用。这意味着我们将丢掉图像边缘与角落的许多图像信息。

为了解决以上两个缺陷，采取的做法是“补全图片”
比如在以上6*6的图像外围再补上一层像素，使得该图片变成8*8的大小，此时再与3*3的filter进行卷积计算后得到的是6*6的输出矩阵，和原始图像一样大小！既消除了图像再卷积计算中不断缩小的缺陷，也使得图像边缘和角落的像素能够多次被使用。这就是卷积操作中的padding.

p = padding 为填充的大小，以上例子p=1,输出的大小就变成了(n+2p-f+1)*(n+2p-f+1)
填充的值一般都设置为0.

填充的大小可以是1也可以是2，那么到底如何判别填多少才是最好的呢？有两个原则可以遵从：valid卷积和same卷积。
valid卷积：即不填充，图片是n*n，filter是f*f, 那么卷积计算以后的矩阵将是(n-f+1)*(n-f+1)
same卷积：即填充到使得输出与输入的图像大小一致

注意：过滤器的大小一般都是奇数
原因是第一，这样可以保证当填充的时候可以对称填充，而不需要左右上下不对称填充
第二，根据计算机视觉的惯例，奇数的过滤器可以有一个中心点，这样在定位过滤器位置的时候比较方便

3.2 卷积步长

卷积中的步长是另一个构建神经网络的基本操作。

之前的例子中过滤器在图像上的移动是每次一个像素，也就是步长为1，我们也可以将补长设置为其他数目，比如2，如下，一个7*7的图像与一个3*3的过滤器进行卷积计算，设置步长为2，则最终会得到一个3*3的输出矩阵。过程如下：

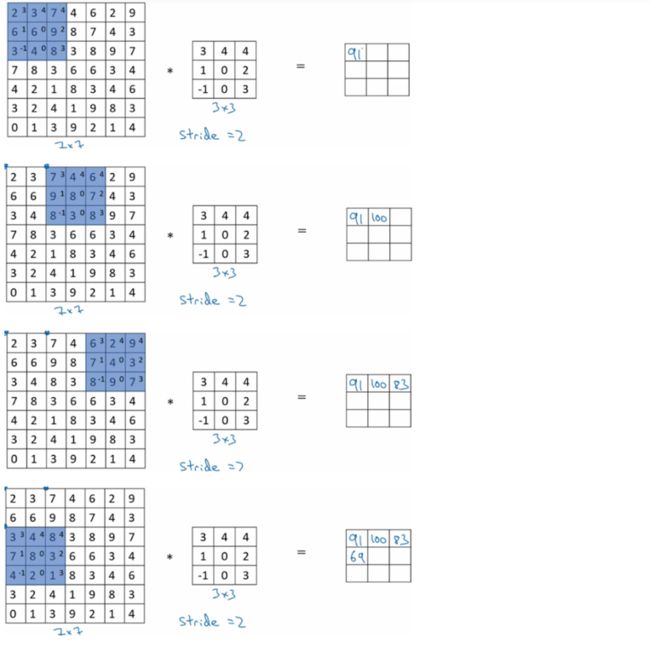
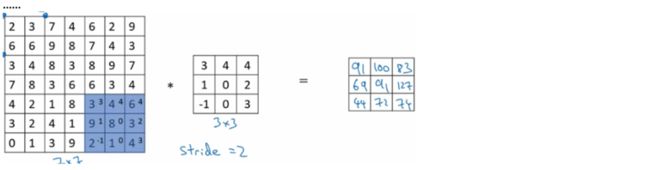
图像大小为n*n，过滤器大小为f*f，stride步长为s，求输出矩阵的大小可以用公式如下表示：

以上公式计算后不为整数的时候，则向下取整。

—————小注意点：
在进入下一节之前来强调一个技术要点，在深度学习的文献中，以上的操作就是卷积运算，但从技术角度来讲这更应该叫做“互相关“，真正的卷积计算，在图像和过滤器相乘之前需要将过滤器进行翻转（镜像转换），即如下变化：

但在机器学习的惯例，我们不对它进行翻转，直接相乘的过程就叫做卷积。因此在本课程中我们做好约定，卷积计算是不做翻转的。

3.3 三维图像上的卷积

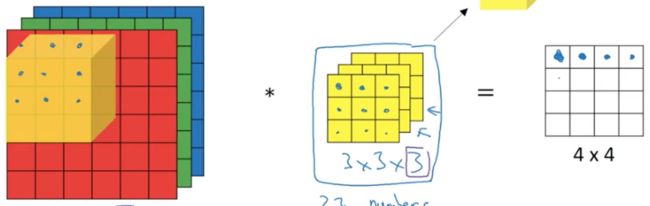
见识了在二维图像上的卷积运算，现在来看看三维立体图像上是如何做卷积运算的。所谓的三维图像，即有3个颜色通道RGB，也就是彩色图像，而前者的二维是黑白图像。

假设有一个6*6*3的图像：

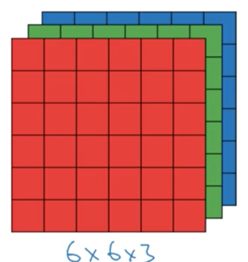
6*6为高*宽，3为颜色通道。

同样有一个3*3*3的卷积核：

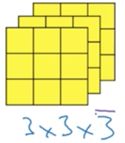
3*3*3分别也表示长宽颜色通道
注意：图片与卷积核的的颜色通道必须是一样大小的

通过卷积之后，会得到一个6*6*1的矩阵（注意不是3）

那是如何进行卷积计算的呢？
将3*3*3的立方体卷积核从图像的左上角开始，颜色通道一一对应，将每一层上的小正方形都对应相乘，然后27个组正方形的乘积求和得到一个数，即为4*4结果矩阵的左上角的第一个数：

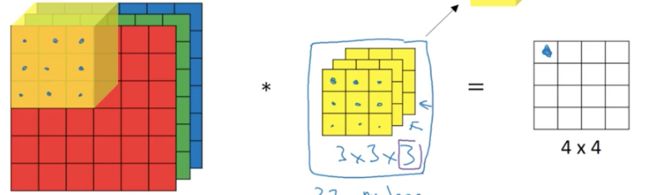
同理，假设步长为1的话，那卷积核就向右移动一步，然后将对应的27个正方形的值相乘得到结果的第2个值：

依次从做到右，从上到下：

直到走完所有路程：

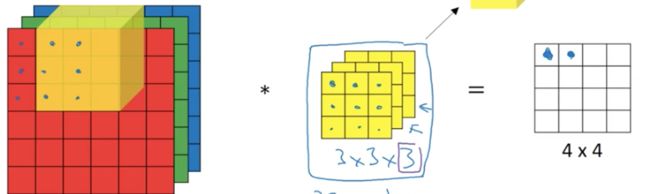
这样的卷积核有什么作用呢？
比如只想要做红色通道中的垂直检测，那么卷积核如下就可以实现：

另外两个通道的卷积值都为0.

如果你对颜色通道不关心，可以在三个颜色通道中都设置垂直检测：

可以检测任何颜色的垂直边缘

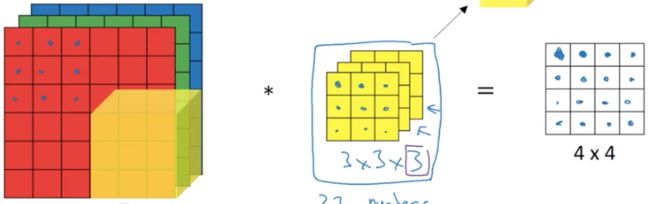
那么你可能会问，如果我想同时检测垂直边缘和水平边缘，或者想检测45度或70度的边缘，怎么办呢？也就是说相同时使用多个过滤器怎么办？看下图：

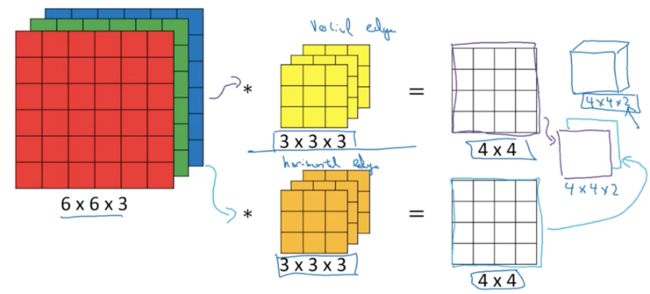
左边仍然是一张6*6*3的图片，过滤器有两个，黄色过滤器是用来检测垂直边缘的，屎色过滤器是用来检测水平边缘的。将他们分别都对图像做一次卷积，于是就输出了两个不同的4*4的结果，将这两个结果叠加，其实就是一个4*4*2的立方体。这就是同时使用多个过滤器的计算过程与结果了。

4.单层卷积网络

4.1 单层卷积网络

(1)计算过程详解
上文中利用两个过滤器做了卷积计算的过程，但一个完整的卷积层可以看成是卷积计算层+激活层的组合。

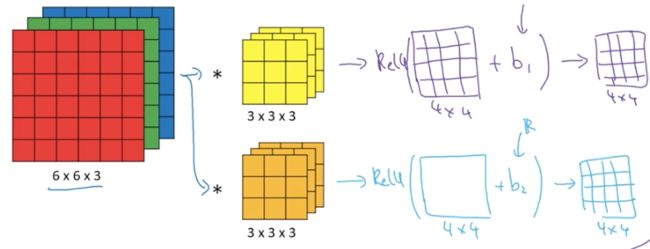
如上图，完成卷积计算得到两个4*4的矩阵结果之后，矩阵中的每个元素（共16个）都分别加上一个bias，再经过一个激活函数（激活函数也是分别作用在每个小正方形上），最终得到一个4*4的结果矩阵。因为有2个过滤器，因此同样也有两个4*4的矩阵输出，叠在一起是4*4*2的小立方体：

以上过程就是一个完整的卷积层的。
当过滤器有n个的时候，输出的立方体大小也为：4*4*n。

将以上过程用公式表示：

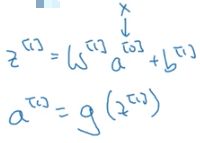
W[1]a[1]是卷积计算的过程，b[1]是bias,z[1]这是一个线性计算的结果；
将z[1]放进激活函数（一般为RELU），得到的结果a[1]为盖层卷积层的最终输出

（2）单程卷积层的参数数目
加入你有10个3*3*3的过滤器在一层卷积神经网络中，那么该层总共拥有多少参数。
每个过滤器有3*3*3=27个参数
每个过滤器有1个bais,因此是28个参数
有10个过滤器，就是10*28=280个参数
因此，无论输入的图像有多大，该层中的参数都是280个。
这是卷积神经网络中的一个特点：避免过拟合。

（3）notation
如果第l层是一个卷积层，
则f[l]表示过滤器的大小

p[l]为padding的大小

s[l]表示步长

n_c[l]表示过滤器的数目

本层的输入

H表示hight， W表示width,C表示channel,[l-1]表示上一层，上一层的输出即本层的输入

本层的输出

本层的输出可以用上一层的输出，本层的pading,filter大小来求得

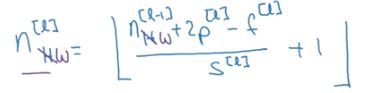
n[c]为本层过滤器的个数。

filter的大小是

本层的通道数，其实就是上一层的输出n_c[l-1],而它正是上一层过滤器的个数。

激活函数的输出值（就是本层的最终输出）：

因此在梯度下降的时候，向量化m个样本的a[l]之后为：

权重的大小（不解释，仔细想想能想通）：

bias的大小

以上notation是比较常用的，但在看论文或者其他资料的时候你也会发现作者不是按照这个套路来的。

4.2 简单卷积网络实例

以一个分类的例子来构建一个简单的卷积神经网络网络

第一层卷积层：
假设你有一张图片，大小是39*39*3：

有10个过滤器，每个过滤器的大小为3*3*3，padding=0, 步长=1

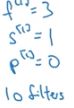
因此激活层的输出为37*37*10
(回顾下37是怎么计算来的：[(n+2p-f)/s] +1)

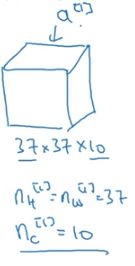
以上是第一层一个卷积层的过程与输出

第二层卷积层：
将第一层的输出作为第二层的输入，利用20个过滤器进行卷积，大小为5*5*10，步长为2，padding=0.

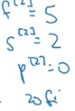
经过激活函数的输出大小为17*17*20
([（37-2*0-5）/ 2] + 1 = 17)

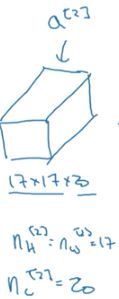
第三层卷积层:
该层有40个过滤器，大小为5*5*20，步长为2，padding=0,经过激活函数后最终输出为7*7*40.

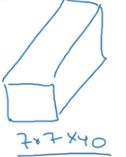
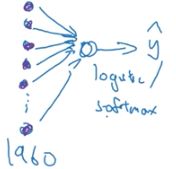
最后一层：
将上一层卷积层的输出7*7*40的向量平摊成1960*1大小的向量。若解决的是二分类问题，则将该向量输入给一个逻辑回归单元，若而多分类则输入给softmax单元。

总过程如图：

5.池化层

池化层往往被用于缩小模型规模，加快训练速度，提高所提取特征的鲁棒性。

5.1 最大池化层计算过程

假如池化层输入的是4*4的矩阵

使用最大池化(max pooling)，输出是一个2*2的矩阵：

这个计算过程，实际上是使用了一个f=2(2*2)的过滤器，s=2(步长为2），得到每一步中图像上2*2区域的最大值作为输出矩阵的一个对应元素。f和s就是最大池化层的超参数。

假如输入矩阵是5*5，f=3,s=2,则输出矩阵为4*4

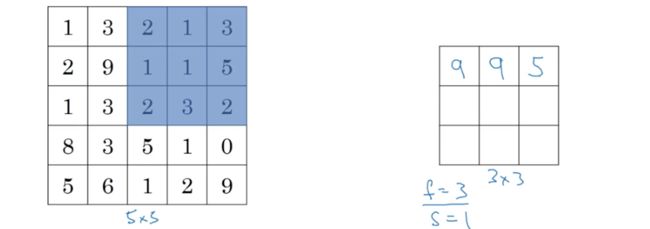
同理，每移动一步，都求该区域内的最大值

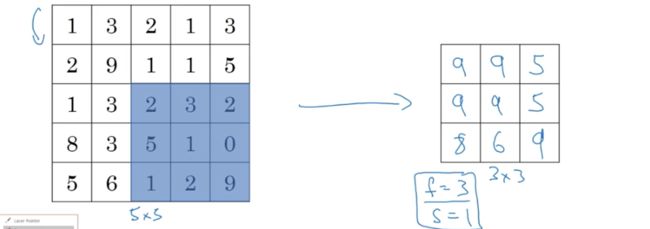
以上是对1维输入进行池化，输出的也是一维的。若输入的是5*5*2，则输出的也应对应为3*3*2，池化计算的过程是一模一样的，只是现在是对每个channel都进行计算。（注意，通道数必须一致）

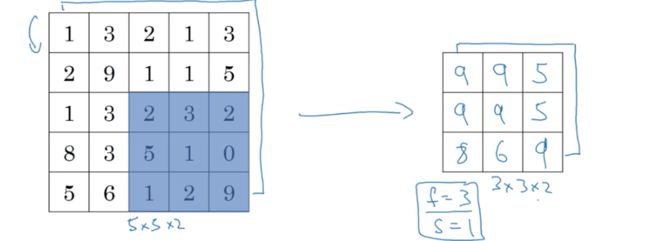
5.2 最大池化层的作用

你可以把4*4的输入看成是某些特征的集合，若数字比较大则可能是提取了某些特定的特征（比如左上角的9可能是一个猫眼探测器），最大池化的作用就是讲输入矩阵中最明显的特征保留在最大池化的输出里。

最大池化在实验中往往表现优秀。

5.3 平均池化层

平均池化层与最大池化层唯一的区别就是前者就均值，后者求最大值而已。入以下例子

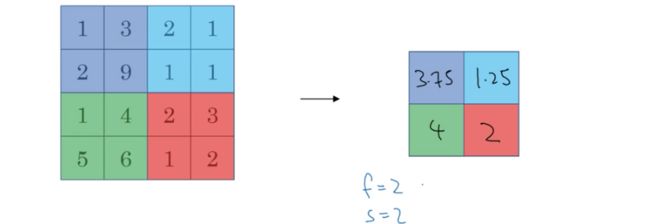
常用的是最大池化层，但如下情况会使用平均池化层：
当神经网络很深很深的时候，你可以用平均池化来分解规模为7*7**1000的网络表示层，在整个空间中求均值，得到1*1*1000的表示。

5.4 对池化层的总结

超参数：
（1）f:filter size 过滤器大小
（2) s:stride 步长
常用的值是f=2,s=2,相当于对原输入缩小了一半进行输出。
f=3,s=2也是比较常用的。

类型：
（1）max pooling 最大池化
（2）average pooling 平均池化

在池化层中padding非常非常非常少用。

因此若池化层的输入为：

则输出为：

在池化层中没有需要反向传播学习的参数。

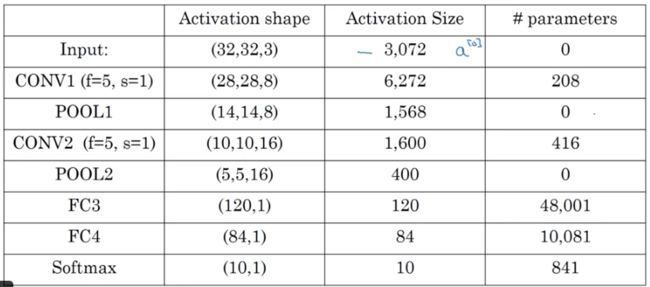
6.卷积神经网络实例(lenet-5)

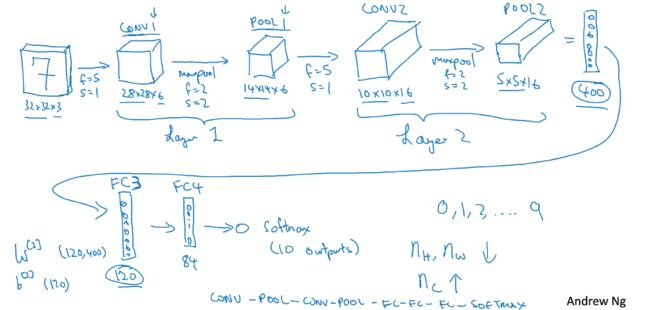
以识别手写数字图片的案例为例，构建一个神经网络能识别图片中的数字为0-9中的哪一个，即是一个多分类的过程。

输入一张32*32*3的图像：

layer1:
经过一个卷积层filter_num=6,f=5, s=1,得到28*28*6;
再经过一个池化层，f=2,s=2,得到14*14*6

注意，一般情况下，我们将一个卷积+一个池化的组合叫做一层。因为池化层本身没有参数，因此其实不能算是一个完整的层。

layer2:
接着，再经过一个卷积层，filter_num=16,f=5,s=1,得到10*10*16
和一个池化层,f=2,s=2,得到5*5*16

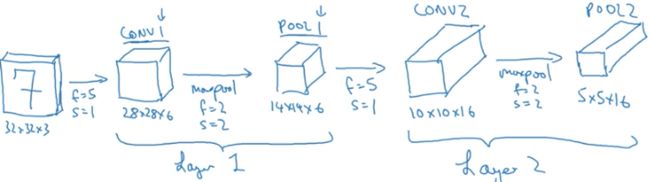
layer3:
将上一层的5*5*16平铺成400*1的向量
进入一个全链接层，该层有120个神经元，因此参数是（120，400）大小

layer4:
将以上输出再进入一个全连接层，该层有84个神经元

layer5:
将以上结果输入softmax层，因为0-9个数字的预测有10类，因此该层有10个神经元。每个神经元的输出代表了图片为对应数字的概率。

总图如下：

以上过程中的图像大小和参数数目的变化如下：

可见，随着神经网络的层数加深，图像的宽和高在神经网络中会越来越小，但是channel会越来越多。

卷积神经网络的另一种常见模式比如：多个卷积层连接，然后是多个池化层连接，再是多个全连接层连接。

超参数的设定：最好不要自己设定超参数，而是查看文献中别人采用了哪些超参数，选一个在别人任务中效果很好的架构，那么它也有可能适用你自己的应用程序。

7.为何卷积神经网络有用

（1）参数共享
一个feature detector（比如垂直边缘检测）如果在图像的一部分中有效，那么也很可能在另外一部分也有效，因此可以共享这个feature detector
（2）稀疏链接
每一层，每一个输出值都只依赖于输入的一小部分（不是全连接）