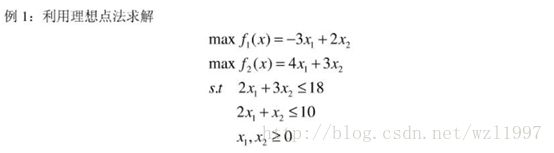多目标线性规划(matlab编程)

多目标规划的类型:

即含有两个或两个以上的目标函数的线性规划叫做多目标规划，现在说说几个简单的解答方法

1.理想点法

简而言之:就是通过先求解每一个目标函数，然后将解放入评价函数里面求解
所用函数为
1.linprog(fun,x0,a,b,aeq,beq,lb,ub)
2.fgoalattain（fun,x0,a,b,aeq,beq,lb,ub)

列子:

clc,clear
f=[3;-2];
a=[2,3;2,1];
b=[18;10];
lb=[0,0];
[x,favl]=linprog(f,a,b,[],[],lb)

x =

    0.0000
    6.0000


favl =

  -12.0000


f=[-4;-3];
a=[2,3;2,1];
b=[18;10];
lb=[0,0];
[x,favl]=linprog(f,a,b,[],[],lb)

x =

    3.0000
    4.0000


favl =

  -24.0000

clc,clear
x0=[1;1];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
x=fmincon('((-3*x(1)+2*x(2)-12)^2+(4*x(1)+3*x(2)-24)^2)^(1/2)',x0,a,b,[],[],lb,ub)
f1=-3*x(1)+2*x(2);
f2=4*x(1)+3*x(2);

x =

    0.5268
    5.6488
f1 =

    9.7171


f2 =

   19.0537

2.最大最小法

function f=mutiplesubjiect(x)
f(1)=3*x(1)-2*x(2);
f(2)=-4*x(1)-3*x(2);
clc,clear
x0=[0;0];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
[x,favl]=fminimax('mutiplesubjiect',x0,a,b,[],[],lb,[])

x =

     0
     6


favl =

   -12   -18

3.目标规划法

goal=[12,24];
weight=[12,24];
x0=[0;0];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
[x,fval]=fgoalattain('mutiplesubjiect',goal,weight,x0,a,b,[],[],lb,[])
x
0.0000
6.0000,

fval=
  
     -12   -18

参考博客:https://blog.csdn.net/wzl1997/article/details/79120323