Multi-Label Zero-Shot Learning with Structured Knowledge Graphs 论文笔记
Multi-Label Zero-Shot Learning with Structured Knowledge Graphs 论文笔记
个人学习笔记,写得可能比较意识流,各位斟酌食用,理解有误的恳请指正
0. Abstract
这是一个多标签零次学习任务(ML-ZSL),对一个输入预测多个unseen类标签。
引入知识图谱来描述多个标签之间的关系。
模型学习一个信息传播机制来建模seen和unseen的类标签之间的相互依赖关系。
1. Introduction
多标签分类的常见做法:
- 转换成多个不相交的二分类问题,但这样做没有建模到标签之间的联系。
- 引入标签之间的先验知识。
- 基于标签嵌入的方法,将输入图片与它们的标签注入一个隐空间,从而利用标签间的关联关系。
然而,第1、2种方法都没办法直接用到ML-ZSL上去,因为它们没办法泛化到unseen类标签上。
反倒是第三种方法通过利用语义空间的标签表达,可以比较容易的适配ML-ZSL。
虽然已经有ML-ZSL的方法提出了,但是这些方法都没有用到结构化的知识。
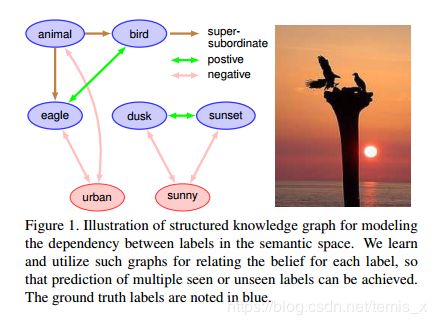
Fig.1 阐述了知识图谱如何帮助多标签的建模。
有一些工作在多标签任务上使用结构化的知识,通常做法为:
- 引入图表达,强迫标签之间有确定的关系
- 利用RNN来建模不同的标签之间的pos / neg 关系
- 通过在知识图谱中传播信息,建模标签之间的关系
本文引入结构化的知识图谱和标签传播机制
3. Approach
3.1. Notations and Overview
D = { ( x i , y i ) } i = 1 N \mathcal{D}=\left\{\left(\mathbf{x}^{i}, \mathbf{y}^{i}\right)\right\}_{i=1}^{N} D={(xi,yi)}i=1N :训练集
N N N :训练样本数
S \mathcal{S} S :训练标签集
U \mathcal{U} U :不可见标签集
训练时, y i ∈ { 0 , 1 } ∣ S ∣ \mathbf{y}^{i} \in\{0,1\}^{|S|} yi∈{0,1}∣S∣ ; 测试时, y ~ ∈ { 0 , 1 } ∣ S ∣ + ∣ U ∣ \tilde{\mathbf{y}} \in\{0,1\}^{|\mathcal{S}|+|\mathcal{U}|} y~∈{0,1}∣S∣+∣U∣
类的语义向量:用 distributed word embedding 表示, W = { w v } v = 1 ∣ S ∣ + ∣ U ∣ \mathbf{W}=\left\{\mathbf{w}_{v}\right\}_{v=1}^{|\mathcal{S}|+|\mathcal{U}|} W={wv}v=1∣S∣+∣U∣ , w v ∈ R d e m b \mathbf{w}_{v} \in \mathbb{R}^{d_{e m b}} wv∈Rdemb , d e m b d_{e m b} demb 是word embedding的维度。在本文总使用GloVe作为word embedding,并且 d e m b = 300 d_{e m b}=300 demb=300 .
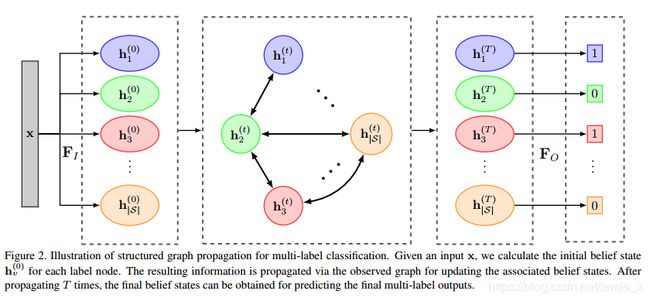
- 每个标签为一个节点, h v ( t ) \mathbf{h}_{v}^{(t)} hv(t) ,初始化状态为 h v ( 0 ) \mathbf{h}_{v}^{(0)} hv(0) (直接从输入 F I \mathbf{F}_I FI获得的)
- 节点 u u u 和节点 v v v 之间连接的权重为 a v u \mathbf{a}_{vu} avu ,由关联函数 F R k \mathbf{F}_{R}^{k} FRk 产生,k表示关系的类型
- 经过 T T T 步传播之后,传入输出函数 F O \mathbf{F}_{O} FO 生成最后的分类概率
3.2 Structured Knowledge Graph Propagation in Neural Networks
- 输入函数 F I ( x , w v ) \mathbf{F}_{I}\left(\mathbf{x}, \mathbf{w}_{v}\right) FI(x,wv) ,其中 x \mathbf{x} x是输入的图片特征, w v \mathbf{w}_v wv 是每个节点 v v v 的Word Embedding,从而得到一个初始的状态置信度 h v ( 0 ) \mathbf{h}_v^{(0)} hv(0) 。这里的 F I \mathbf{F}_I FI 用神经网络来实现。
- 知识图谱的传播权重矩阵 A ∈ R ∣ S ∣ d h i d × ∣ S ∣ d h i d \mathbf{A} \in \mathbb{R}^{|\mathcal{S}| d_{h i d} \times|\mathcal{S}| d_{h i d}} A∈R∣S∣dhid×∣S∣dhid ,通过邻接节点来获得每个节点的更新向量 u v ( t ) \mathbf{u}_{v}^{(t)} uv(t) ,然后通过门限机制GRU来更新。
上面两步用数学语言来表示:
h v ( 0 ) = F I ( x , w v ) u v ( t ) = tanh ( A v ⊤ [ h 1 ( t − 1 ) ⊤ … h ∣ S ∣ ( t − 1 ) ⊤ ] ⊤ ) h v ( t ) = G R U C e l l ( u v ( t ) , h v ( t − 1 ) ) \begin{aligned} \mathbf{h}_{v}^{(0)} &=\mathbf{F}_{I}\left(\mathbf{x}, \mathbf{w}_{v}\right)\\ \mathbf{u}_{v}^{(t)} &=\tanh \left(\mathbf{A}_{v}^{\top}\left[\mathbf{h}_{1}^{(t-1) \top} \ldots \mathbf{h}_{|S|}^{(t-1) \top}\right]^{\top}\right) \\ \mathbf{h}_{v}^{(t)} &=G R U C e l l\left(\mathbf{u}_{v}^{(t)}, \mathbf{h}_{v}^{(t-1)}\right) \end{aligned} hv(0)uv(t)hv(t)=FI(x,wv)=tanh(Av⊤[h1(t−1)⊤…h∣S∣(t−1)⊤]⊤)=GRUCell(uv(t),hv(t−1))
GRUCell的更新过程为:
z v ( t ) = σ ( W z u v ( t ) + U z h v ( t − 1 ) + b z ) r v ( t ) = σ ( W r u v ( t ) + U r h v ( t − 1 ) + b r ) h ~ v ( t ) = tanh ( W h u v ( t ) + U h ( r v ( t − 1 ) ⊙ h v ( t − 1 ) ) + b h ) h v ( t ) = ( 1 − z v ( t ) ) ⊙ h v ( t − 1 ) + z v ( t ) ⊙ h ~ v ( t ) \begin{aligned} \mathbf{z}_{v}^{(t)} &=\sigma\left(\mathbf{W}^{z} \mathbf{u}_{v}^{(t)}+\mathbf{U}^{z} \mathbf{h}_{v}^{(t-1)}+\mathbf{b}^{z}\right) \\ \mathbf{r}_{v}^{(t)} &=\sigma\left(\mathbf{W}^{r} \mathbf{u}_{v}^{(t)}+\mathbf{U}^{r} \mathbf{h}_{v}^{(t-1)}+\mathbf{b}^{r}\right) \\ \tilde{\mathbf{h}}_{v}^{(t)} &=\tanh \left(\mathbf{W}^{h} \mathbf{u}_{v}^{(t)}+\mathbf{U}^{h}\left(\mathbf{r}_{v}^{(t-1)} \odot \mathbf{h}_{v}^{(t-1)}\right)+\mathbf{b}^{h}\right) \\ \mathbf{h}_{v}^{(t)} &=\left(1-\mathbf{z}_{v}^{(t)}\right) \odot \mathbf{h}_{v}^{(t-1)}+\mathbf{z}_{v}^{(t)} \odot \tilde{\mathbf{h}}_{v}^{(t)} \end{aligned} zv(t)rv(t)h~v(t)hv(t)=σ(Wzuv(t)+Uzhv(t−1)+bz)=σ(Wruv(t)+Urhv(t−1)+br)=tanh(Whuv(t)+Uh(rv(t−1)⊙hv(t−1))+bh)=(1−zv(t))⊙hv(t−1)+zv(t)⊙h~v(t)
其中 W , U , b \mathbf{W}, \mathbf{U}, \mathbf{b} W,U,b 都是可学习的。
- 输出函数 F O \mathbf{F}_{O} FO, 用全连接神经网络实现,对于每个标签节点都可以获得一个置信度 p p p :
p v ( t ) = F O ( h v ( t ) ) p_{v}^{(t)}=\mathbf{F}_{O}\left(\mathbf{h}_{v}^{(t)}\right) pv(t)=FO(hv(t))
3.3 传播矩阵A的学习
本节阐述如何合理地将邻接节点的信息结合起来,构建A矩阵。
在A中,邻接节点的权重设为非零,不相邻的节点权重设为0。
不是为相同类型/关系的边分配相同的传播权重,而是分配产生传播权重的相同关系函数 F R k \mathbf{F}_R^k FRk,其中k表示边类型,即相同类型的边有相同类型的关联函数:
a v u = F R k ( w v , w u ) \mathbf{a}_{v u}=\mathbf{F}_{R}^{k}\left(\mathbf{w}_{v}, \mathbf{w}_{u}\right) avu=FRk(wv,wu)
传播机制如下图:
这样,这个F函数学习了一个从语义Word Embedding空间到传播矩阵的一个映射,从而有依据地建模关联边之间依赖关系。
用在ZSL中,可以从语义空间学习可以让模型生成unseen类的类标签。
3.4 从ML到ML-ZSL
loss:binary cross-entropy(BCE)
L = 1 N 1 ∣ S ∣ ∑ i , v , t α ( t ) ( ( y v i log p v ( t ) + ( 1 − y v i ) log ( 1 − p v ( t ) ) ) \mathcal{L}=\frac{1}{N} \frac{1}{|\mathcal{S}|} \sum_{i, v, t} \alpha(t)\left(\left(y_{v}^{i} \log p_{v}^{(t)}+\left(1-y_{v}^{i}\right) \log \left(1-p_{v}^{(t)}\right)\right)\right. L=N1∣S∣1i,v,t∑α(t)((yvilogpv(t)+(1−yvi)log(1−pv(t)))
其中, α ( t ) = 1 / ( T − t + 1 ) \alpha(t)=1 /(T-t+1) α(t)=1/(T−t+1) ,它是随着t的增加而增大的,表示越靠后的越准确,并且这个loss是把每一步t的置信度都进行加权了。
但是,测试时,只用最后步骤T的置信度 p v ( T ) p_{v}^{(T)} pv(T) 作为输出。
对于ML-ZSL,把A扩展到 A ~ ∈ R ( ∣ S ∣ + ∣ U ∣ ) d h i d × ( ∣ S ∣ + ∣ U ∣ ) d h i d \tilde{A} \in \mathbb{R}^{(|\mathcal{S}|+|\mathcal{U}|) d_{h i d} \times(|\mathcal{S}|+|\mathcal{U}|) d_{h i d}} A~∈R(∣S∣+∣U∣)dhid×(∣S∣+∣U∣)dhid ,编码知识图谱中unseen的类标签的关系。
那么,更新向量就变成:
u v ( t ) = tanh ( A ~ v ⊤ [ h 1 ( t − 1 ) ⊤ … h ( ∣ S ∣ + ∣ y ∣ ) ( t − 1 ) T ⊤ ) , ∀ v ∈ S ∪ U \mathbf{u}_{v}^{(t)}=\tanh \left(\tilde{\mathbf{A}}_{v}^{\top}\left[\mathbf{h}_{1}^{(t-1) \top} \ldots \mathbf{h}_{(|S|+|y|)}^{(t-1)} T^{\top}\right), \forall v \in \mathcal{S} \cup \mathcal{U}\right. uv(t)=tanh(A~v⊤[h1(t−1)⊤…h(∣S∣+∣y∣)(t−1)T⊤),∀v∈S∪U
输入输出函数与3.2节一致。
ML-ZSL传播机制如图4所示。
- 从图片拿到一个图像特征x,每个节点都将该图像特征传入一个神经网络,输出一个是否包含这个节点表示的类的概率。**(我猜测是学习一个从图像特征到Word Embedding的映射,这样unseen节点也可以学习)**这样,获得了KG每个节点的初始值。这个过程其实每个节点都是一个分类器,会不断地训练这个分类器的权重。
- 每个节点(seen和unseen)的初始值确定后,接着确定邻接矩阵A的每条边的权重:
- 从WordNet获得super-subordinate的联系
- 计算每个标签对之间的WUP相似度来确定是什么类型的关联关系,来确定使用什么类型的关联函数
- 确定关联类型之后,相同关联关系的标签对共享同一个关联函数 F R k \mathbf{F}_R^k FRk ,计算A矩阵里的每个点的权重
- 确定A后,即可进行标签传播,计算出对应 u v ( t ) \mathbf{u}_v^{(t)} uv(t),然后根据GRU门限计算出下一步的 h v ( t ) \mathbf{h}_v^{(t)} hv(t)
- 对于每一步的 h v ( t ) \mathbf{h}_v^{(t)} hv(t) ,都有一个由全连接网络构成的输出层(输出函数 F O \mathbf{F}_O FO),输出图片中包含v代表的类的概率
- 最后对每一步每个节点的BCEloss进行加权,得到最后的loss,在反向传播回去,调整 F O F_O FO (全连接层), G R U C e l l GRUCell GRUCell ,输入函数 F I \mathbf{F}_I FI 。
总的来说,这个过程,其实是学习一个带有知识图谱的多标签分类器。
4. Experiment
4.1 Building the Knowledge Graph
Word Embedding:WordNet
标签关联类型,3种:
- super-subordinate(可以直接从WordNet提取)
- positive
- negative
对于pos、neg的标签相似度用WUP相似度计算。
在下面的实验中,KG一共有5步,即T=5.
4.2 数据集与Settings
数据集:NUS-WIDE(特别为ML-ZSL使用的)和Microsoft COCO(MS-COCO)
NUS-WIDE(网络图片数据集)
- 数量:共收集到269,648张,筛选后剩90360张图片
- 标签来自Flickr.
- 标签由1000个从网上收集的噪音标签和81个高质量的标签,分别把两个标签集命名为NUS-1000和NUS-81
- 去掉没有标签的图片
从图片中,使用ResNet-152来提取出2048-d的图像特征x。
数据集划分:
- 训练集75000张,验证集5000张,测试集10360张
MS-COCO:
- 大尺寸数据集
- 数据划分,遵循2014比赛的划分
- 82783张训练,40504张测试
- 移除没有标签的图片后,得到78081张训练图片,4000验证图片,40137张测试图片
- 标签:80个
- 同样使用ResNet-152提取2048-d的图像特征x
4.3 多标签分类任务
先来看ML的效果。
图片的标签tag都有排序,选择Top K的标签,这里K=3
验证集用来选一个合适的概率阈值来预测标签。
指标:precision(P)和recall(R)和F1
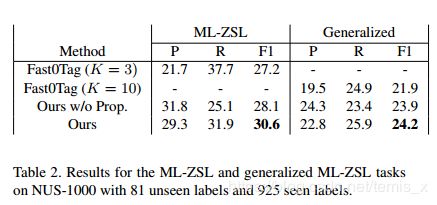
4.4 ML-ZSL and Generalized ML-ZSL
NUS-WIDE
unseen类:81个
seen:1000