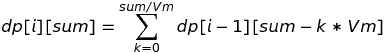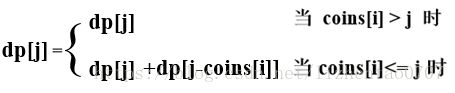硬币拼凑指定面额的动态规划算法

 

拼凑钱币

题目来源：美团点评2017秋招笔试题

题目描述：
给你六种面额1、5、10、20、50、100元的纸币，假设每种币值的数量都足够多，编写程序求组成N员（N为0-10000的非负整数）的不同组合的个数。
输入描述:
输入为一个数字N，即需要拼凑的面额
输出描述:
输出也是一个数字，为组成N的组合个数。
示例1
输入
5
输出

2

解题思路：

这个题的思路是动态规划的算法思路，如果用二维的则会超时，采用一维的则首先对币种遍历，每遍历一个币种coins[i]，然后再对1，N（需要拼凑的钱数）进行依次遍历，其实就转化为N-coins[i]的问题了，这样就可以计算总的方案数。该动态规划的状态转移方程：dp[j]=dp[j]+dp[j-coins[i]](前提条件是j-coins[i]>=0)。

详细说明

给定一个数值sum，假设我们有m种不同类型的硬币{V1, V2, ..., Vm}，如果要组合成sum，则

                          sum = x1 * V1 + x2 * V2 + ... + xm * Vm 

求所有可能的组合数，就是求满足前面等值的系数{x1, x2, ..., xm}的所有可能个数。

我们希望用m种硬币构成sum，根据最后一个硬币Vm的系数的取值无非有这么几种情况，xm分别取｛0, 1, 2, ..., sum/Vm｝，换句话说，上面分析中的等式和下面的几个等式的联合是等价的。

sum = x1 * V1 + x2 * V2 + ... + 0 * Vm

sum = x1 * V1 + x2 * V2 + ... + 1 * Vm

sum = x1 * V1 + x2 * V2 + ... + 2 * Vm

...

sum = x1 * V1 + x2 * V2 + ... + K * Vm  

　　其中K是该xm能取的最大数值K = sum / Vm。可是这又有什么用呢？不要急，我们先进行如下变量的定义：

dp[i][sum] = 用前i种硬币构成sum 的所有组合数。

　　那么题目的问题实际上就是求dp[m][sum]，即用前m种硬币（所有硬币）构成sum的所有组合数。在上面的联合等式中：当xm=0时，有多少种组合呢？ 实际上就是前i-1种硬币组合sum，有dp[i-1][sum]种！ xm = 1 时呢，有多少种组合？ 实际上是用前i-1种硬币组合成(sum - Vm)的组合数，有dp[i-1][sum -Vm]种; xm =2呢， dp[i-1][sum - 2 * Vm]种，等等。所有的这些情况加起来就是我们的dp[i][sum]。所以：

dp[i][sum] = dp[i-1][sum - 0*Vm] + dp[i-1][sum - 1*Vm]  + dp[i-1][sum - 2*Vm] + ... + dp[i-1][sum - K*Vm]; 其中K = sum / Vm

归纳成数学表达式即为：

如果我们用二位数组表示dp[i][sum], 我们发现第i行的值全部依赖与i-1行的值，所以我们可以逐行求解该数组。如果前0种硬币要组成sum，我们规定为dp[0][sum] = 0. （通过此分析可知该思路实质上是动态规划）。

C++代码实现如下：

/****************************************************************
 * coin Combinations: using dynamic programming
 *
 * Basic idea:
 * dp[i][j] = sum(dp[i-1][j-k*coins[i-1]]) for k = 1,2,..., j/coins[i-1]
 * dp[0][j] = 1 for j = 0, 1, 2, ..., sum
 *
 * Input:
 * coins[] - array store all values of the coins
 * coinKinds - how many kinds of coins there are
 * sum - the number you want to construct using coins
 *
 * Output:
 * the number of combinations using coins construct sum
 *
 * Usage:
 * c[3] = {1, 2, 5};
 * int result = coinCombinations(c, 3, 10);
 *
 ****************************************************************/
int coinCombinations(int coins[], int coinKinds, int sum)
{
	// 2-D array using vector: is equal to: dp[coinKinds+1][sum+1] = {0};
	vector > dp(coinKinds + 1);
	for (int i = 0; i <= coinKinds; ++i)
	{
		dp[i].resize(sum + 1);
	}
	for (int i = 0; i <= coinKinds; ++i)
	{
		for (int j = 0; j <= sum; ++j)
		{
			dp[i][j] = 0;
		}
	}
	//init: dp[i][0] = 1; i = 0, 1, 2 ..., coinKinds
	//Notice: dp[0][0] must be 1, althongh it make no sense that
	//using 0 kinds of coins construct 0 has one way. but it the foundation
	//of iteration. without it everything based on it goes wrong
	for (int i = 0; i <= coinKinds; ++i)
	{
		dp[i][0] = 1;
	}
	// iteration: dp[i][j] = sum(dp[i-1][j - k*coins[i-1]])
	// k = 0, 1, 2, ... , j / coins[i-1]
	for (int i = 1; i <= coinKinds; ++i)
	{
		for (int j = 1; j <= sum; ++j)
		{
			dp[i][j] = 0;
			for (int k = 0; k <= j / coins[i - 1]; ++k)
			{
				dp[i][j] += dp[i - 1][j - k * coins[i - 1]];
			}
		}
	}
	return dp[coinKinds][sum];
}

另一种思路  

假设dp[i][j]表示前i种纸币构成值为j的所有组合总数，则对于第i种纸币来说，有三种种情况：

(1) 当 coins[i] > j 时，无法构成值 j，此时dp[i][j] = dp[i-1][j]； 

(2) 当 coins[i] = j 时，dp[i][j] = dp[i-1][j-coins[i]]+1;（coins[i] = j 时，coins此种纸币即可构成值 j）

(2) 当 coins[i] < j 时，对于第 i 种纸币来说有两种选择：用或不用；

       a. 不用：dp[i][j] = opt[i-1][j]；前 i 种纸币可构成 j 的最大组合数即是前 ( i - 1) 种纸币可构成 j 的最大组合数；

       b. 用： dp[i][j] = dp[i][j-coins[i]]；前 i 种纸币可构成 j 的最大组合数即是前( i - 1 )种纸币构成值为(j - coins[i])的最大组合数。

综上，状态转换方程如下：

#include 
#include 
 
using namespace std;
 
int main()
{
	int n;
	cin >> n;
	vector coins(n, 0);
	for (auto &m : coins)
		cin >> m;
	int sum;
	while (cin >> sum)
	{
		vector> dp(n, vector(sum + 1, 0));
		for (int j = 1; j <= sum; j++)
			dp[0][j] = 1;
		for (int i = 1; i < n; i++)
		{
			for (int j = 1; j <= sum; j++)
			{
				if (coins[i] > j)
					dp[i][j] = dp[i - 1][j];
				else if (coins[i] < j)
					dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
				else
					dp[i][j] = dp[i - 1][j] + 1;
			}
		}
		cout << dp[n - 1][sum] << endl;
	}
	return 0;
}

 

上述方法的时间复杂度和空间复杂度均为O(n*sum)，其中空间复杂度是可以优化到O(sum)的。状态方程如下：

令dp[0] = 1，上式可以简化为：

优化后的代码如下： 

int coinCombinations1(int n, vector coins, int sum)
{
	vector> dp(n, vector(sum + 1, 0));
	for (int j = 1; j <= sum; j++)
		dp[0][j] = 1;
	for (int i = 1; i < n; i++)
	{
		for (int j = 1; j <= sum; j++)
		{
			if (coins[i] > j)
				dp[i][j] = dp[i - 1][j];
			else if (coins[i] < j)
				dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
			else
				dp[i][j] = dp[i - 1][j] + 1;
		}
	}
	return dp[n - 1][sum];
}