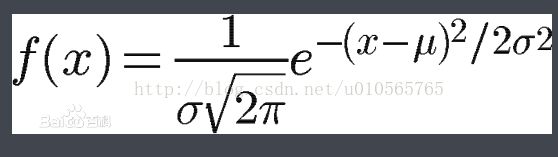滤波器的使用和经常出现的噪声(https://shop137138656.taobao.com/?spm=2013.1.1000126.d21.c3995851hkvlEt)
经常出现的噪声:
1:椒盐噪声:出现的位置是随机的,但噪声的赋值是基本相同的。(含有随机出现的黑白强度值,)
2,高斯噪声:出现的位置是一定的(每一个点上),但噪声的幅值是随机的。(高斯噪声含有强度服从高斯或正态分布的噪声)(瑞利噪声也这样)
3,脉冲噪声,(含由随机的白强度值(正脉冲噪声))或黑强度值(负脉冲噪声),
4,从统计学的观点看,凡是统计特征不随时间变化的噪声称为平稳噪声,而随特征随时间变化的噪声称为非平稳噪声,
噪声说明:
1)噪声是不可预测的随机信号,通常采用概率统计方法对其进行分析。
使用滤波器的心得:
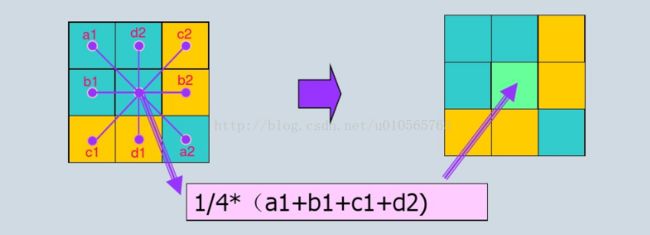
1)中值适合处理椒盐噪声,选择合适的中点来代替当前的点;均值适合处理高斯噪声,将噪声平均化,降低噪声;在使用中值的时候,获得的中值信号有时不太理想,这时候不妨将中值进行一下均值处理,获得的数据获取会更好些。
关键的一点:滑动平均数字滤波参数的研究
1)滑动平均滤波器中窗口中的点数的设置和认识一般停留子啊经验
水平上,文献《互动平均数字滤波参数研究》得出:滑动平均点数N与分频值Wc(滤波截止频率Fc/信号采样频率Fs)之间的计算公式。这个Wc分频值为小于0.5的值。因为信号的最大频率为信号采样频率的一半,截止频率肯定比信号的最大频率要小。
2)其中得到的结论: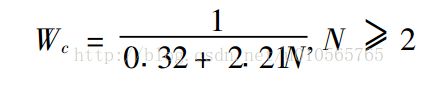 Wc(滤波截止频率Fc/信号采样频率Fs)
Wc(滤波截止频率Fc/信号采样频率Fs)
注意:这还得根据实际情况使用,并不一定使用于实际的现象。
1,小波滤波器,在其他的文章中已经试验了几个了,这里测试其他的滤波器
这种方法,虽然有实时性,但是在一些尖峰点处,由于受到附近相邻点的干扰,导致信号出现尖峰,这干扰到了信号的检测,对于ecg,去除基线漂移,尽量避免不必要的增添信号。
3,中值滤波:(只处理一维信号)一种非线性平滑技术,
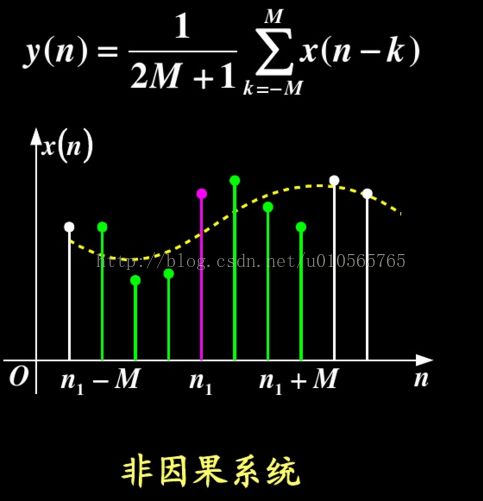
1)原理是:把数字序列中一点的值用该点的一个领域内个点值的中值来代替。,如果一个信号是平缓变化的,那么某一点的输出值可以用这点的某个大小的邻域内的所有值的统计中值来代替(让周围的像素值接近真实值,从而消除孤立的噪声点),这个邻域在信号处理领域称之为窗(window)。窗开的越大,输出的结果就越平滑,但也可能会把我们有用的信号特征给抹掉。所以窗的大小要根据实际的信号和噪声特性来确定。
先对信号进行延拓k(从这里可以看到窗口的宽度是2*k+1),将边界点的数值向前后向后延拓一定的长度;之后对x(n-k) 到x(n+k)范围内的数据进行排序,取其中的中值,代表当前的点。
2)关键点:选择合适的滤波器宽度,中值滤波是非线性的。
3)在matlab中使用的是一维中值滤波器:y = medfilt1(x,N),输入一维信号,将一维信号按列输入,矩阵也按列处理。其中的N,如果没有指定,默认使用N= 3,如果N为奇数:y(k)是x(k-(N-1)/2:k+(N-1)/2);对于偶数:y(k)是x(k-N/2:k+N/2-1)的中值。
4)中值滤波器:在进行边缘检测的过程中通常进行一定程度的降噪,进行图像处理中的一个常用的步骤,它对于斑点噪声,椒盐噪声,尤为重要,在不希望出现边缘模糊的场合很有用。
5)中值滤波对脉冲噪声有良好的作用,特别是在滤除噪声的同时,能够保护信号的边缘,使之不被模糊。这些优良特性在线性滤波方法所不具有的。中值滤波是在“”最小绝对误差”准则下的最优滤波。这是一种基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术。
6)中值滤波器的特性:a:中值滤波器在图像处理中比较多,
b,边界值的处理:常见的方法有:不处理边界数据,原样输出;将边界值重复;前后补0;在边界时缩小窗的大小。
c,中值滤波器是一种在去除噪声的同时能较好的保护图像边缘细节的非线性技术,在图形增强和恢复等领域得到了广泛的应用。中值滤波在处理图形的时候,既可以除噪,又可以较好的得到图形的复原效果。
d,中值滤波器是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术,这种滤波器的优点是:简单而且速度快,在滤除叠加白噪声和长尾噪声叠加噪声的方面显示了几号的性能,同时很好的保护了图像边缘,使图像可以较好的复原,同时,中值滤波器可以很容易的自适应化,从而进一步提高其滤波性能。
e,在窗口中单调增加或者单调递减的序列,中值滤波输出信号仍保持输入信号不变,利用这个特点,可以是中值滤波既能去除图像中的噪声,又能保持图像中的一些物体的边缘。
f,对零均值正态分布的噪声输入,中值绿币输出和输入噪声的密度分布有关,输出噪声方差和输入噪声密度函数的平方比成反比。对堆积噪声的抑制能力,中值滤波性能要比平均值滤波效果差些。但对于脉冲干扰来讲,特别是脉冲宽度小于m/2,相聚较远的窄脉冲,中值滤波很有效。(对随机的抑制力差些,对脉冲的好些)
g,中值滤波是非线性的,经过中值滤波后,频谱基本不变。图像经过中值滤波后,可以消除图像上的各种随机噪声,利用中值滤波可以很好的消除这些干扰。
h,中值滤波器窗口的宽度要从小到大实验,选择较好的效果的长度。中值滤波器的效果受滤波窗口尺寸的影响较大,在消除噪声和保护图像的细节存在矛盾:滤波窗口较小,则能很好的保护图形中的某些细节,但对噪声的过滤效果就不是很好;反之,窗口尺寸较大有较好的噪声过滤效果,但是对图像造成一定的模糊,另外,根据中值滤波器的原理,如果在滤波窗口内的噪声点的个数大于整个窗口内像素的个数,则中值老伯伯就不能很好的过滤掉噪声。(由此,对于心电信号,窗口较小,细节可以保留,但是去噪不好,窗口较大,细节受损,滤波较好。)
i,中值滤波器绝对阻止噪声峰值,因为中值滤波只取中位数,绝对不会取异常数;这种滤波器克服了线性滤波的局限性,处理图像是,线性滤波将破坏边缘,不能有效的滤除脉冲噪声。中值滤波绝对阻止噪声峰值;有效抑制随噪;在非平稳的信号的处理中取得了较大的成功;引入假高频成分,且各频段的振幅值发生了变化;会引发信号的畸变,在做地震资料进行中值滤波时,最好做一次低通滤波,以消除这些假高频的影响;中值滤波实际上是一个平滑滤波,经过其处理后,主频向低频移动,高频成分受到损害,正是由于其平滑作用,使处理后的地震数据波形过于一致而显呆板,有一些信息不可能客观的反应出来;中值滤波的一个严重不足时引起相对滤波窗口而言较为‘’细小"的细节结构的破坏和丢失。
j:中值滤波器是低通滤波器,中值滤波取中值为序列的输出,可以看做是对数据序列进行局部平滑,实质就是低通低通滤波。噪声抑制和细节保留之间存在矛盾,抑制噪声能力加强,很多细节丢失。
实例:void middle_filter(float *sig, int segLen, float *I_out)
{
int width = 250;
float *buf = new float[segLen + width];
//将信号进行延拓
for (int i = 0; i < (segLen+width-1); i++)
{
if (i < width / 2)
{
buf[i] = sig[1];
}else if (i<(segLen+width/2))
{
buf[i] = sig[i-width/2];
}
else
{
buf[i] = sig[segLen -1];
}
}
//将信号进行中值滤波
float *begin_data = new float[width+1];
for (int m = width / 2; m < segLen+width/2; m++)
{
int i = 0;
for (int j = 0; j < width + 1; j++)
{
begin_data[j] = buf[m-width/2+i];
i++;
}
//排序
sort(begin_data, begin_data+width);
I_out[m - width / 2] = sig[m - width / 2] - begin_data[width / 2];
}
delete[] begin_data;
delete[] buf;
,
}这个算法还是有优化的余地,将其中的循环进行二分查找,赋值使用memcpy,可以提速很快。这个函数的作用是:先依据中值滤波函数找出基线漂移的数据,之后用带噪声的信号减去基线漂移的数据,获得需要的数据 。
注意:通过寻找数据中的中值,将数值较大的值用较低的值来代替,原来的数据减去较低的值,相当于原始信号减去低频信号(数值小,频率低);即去除了基线漂移。
4,自适应中值滤波:
1)使用两个进程来进行计算自适应中值滤波。
- Zmin=Sxy中的最小灰度值
- Zmax=Sxy中的最大灰度值
- Zmed=Sxy中的灰度值的中值
- Zxy表示坐标(x,y)处的灰度值
- Smax=Sxy允许的最大窗口尺寸
进程A:
A1=Zmed-Zmin
A2=Zmed-Zmax
如果A1>0且A2<0,则转至进程B
否则增大窗口尺寸
如果窗口尺寸<=Smax,则重复进程A
否则输出Zmed
进程B:
B1=Zxy-Zmin
B2=Zxy-Zmax
如果B1>0且B2<0,则输出Zxy
否则输出Zmed
原理说明:过程a的目的是:确定当前的窗口内得到的Zmed是否是噪声,如果Zmin 如果在过程A中,得到则Zmed不符合条件Zmin 噪声出现的概率较低时,自适应中值滤波器可以较快的得出结果,不需要增加窗口的尺寸;反之,噪声出现的概率较高时,需要增大窗口尺寸,这也符合中值滤波器的特点;噪声比较多时,需要更大的滤波器窗口尺寸。 2)自适应滤波是今年来一种最佳的滤波算法,实在维纳滤波,kalman滤波等线性滤波基础上发展起来的一种最佳的滤波算法。有更强的适应性和更优的滤波性能。 自适应滤波的研究对象是具有不确定的系统或信息过程。这里的不确定性指所研究的处理信息过程及其环境的数学模型不是完全确定的。任何一个实际的信息过程都具有不同程度的不确定性,这些不确定性有时表现在过程内部,有时变现在过程外部。从过程内部来讲:描述研究对象即信息动态过程的数学模型的结构和参数是设计者实现并不一定确切知道的。不确定的噪声和扰动造成信号的不确定性,在综合处理该信息的过程中,使用一些指定的性能指标达到最优或近似最优。 3)基本原理:中值滤波,在噪声的密度不是很大的情况下,效果不错。但是当概率出现较高时,常规的中值滤波的效果就不好了。有一个选择就是增大滤波器的窗口的大小,这虽然在一定的程度上能解决上述的问题,但是会给图像造成较大的模糊。 常规的中值滤波器的窗口尺寸是固定不变的,就不能同时兼顾去噪和保护图像细节。这是就要寻求一种改变,在滤波的过程中,动态的改变滤波器的窗口尺寸的大小,这就是自适应中值滤波器。在滤波的过程中,自适应中值滤波器会根据预先设定好的条件,改变滤波窗口的尺寸大小,同时还会根据一定的条件判断当前的像素是不是噪声,如果是则用邻域中值替换当前的像素,不是,则不改变。 4)自适应中值滤波有三个目的:滤除椒盐噪声 平滑其他非脉冲噪声,尽可能的保护图像中的细节信息,避免图像边缘的细化或者粗化。 自适应中值滤波算法,不但能消除概率较大的椒盐噪声,而且能很好的保护图像的细节。这是常规的中值滤波器做不到的,自适应中值滤波需要一个矩形的窗口Sxy,和常规的中值滤波器不同的是这个窗口的大小会在滤波处理过程中进行改变。 中值滤波器和自适应中值滤波器的比较:使用中值滤波器的作用是获得信号中低频中的数据,通过改变窗口的大小获得低频数据(就是用中值代替较大的值),之后用原始数据减去基线的低频数据,获得去除基线的值。窗口的大小来自经验值。自适应中值滤波器获得的数据并不是将所有的数据都转换为低频数据点,因此不能明确的找出其中的低频成分,这样就不能获得低频信号,就不能用原信号减去获得的值,得不到去除基线的信号。 5,将信号中的发生重大变化的部分找出来,根据相似性,找到发生变化严重的地方,认为这是受到干扰的部分,将这段数据进行滤波,然后将数据根据幅值变化原来的幅值,将图像返回去。只变动发生重大变化的部分,其他的地方不动。(先试试) 6,均值滤波器:在图像上,对待处理的像素给定一个模板,该模板保罗了其周围的邻近像素,将模板中的全体像素的均值来替代原来的像素值的方法。 均值滤波器的缺点:回收图形变的模糊,原始是它对所有的点都是同等对待,将噪声点分摊的同时,将景物的边界点也分摊了。 为了改善效果,就可以采用加权平均的方式来构造滤波器。 7,均值滤波器和中值滤波器比较:椒盐噪声是赋值近似相等,但是随即分布在不同位置上,图像中有干净点,也有污染点。中值滤波是选择适当的点来替代污染点,处理效果好,因为噪声的均值不为0,所以均值滤波不能很好的去除噪声点。 对用户高斯噪声,均值滤波效果比中值滤波效果好。 原因:高斯噪声是幅值近似正太分布,单分布在每点像素上,因为图像中的每点都是污染点,所以中值找不到合适的干净点,因为正太分布的均值为0,所以均值滤波可以消除高斯噪声,。 8,边界保持类平滑滤波器:KNN平滑滤波器(就是找到某个点附件的一些点,求均值代替当前的点):经过平滑滤处理后的图像,就会变得模糊,:分析原因:在图像上的景物之所以可以辨认清楚,是因为目标物之间存在边界。而边界点和噪声点有一个共同的特点是:都具有灰度的跃变特性。所以平滑处理会同时将边界也处理了。(个人认为:对于将长的信号,比如24小时的ECG,将边界延长点,就不会干扰边界的特点了。)平滑滤波器;有了边界的保持的租用,素来以在去除椒盐以及高斯噪声时,对图像景物的清晰度保持方面的及效果非常明显。付出的代价是:算法的复杂度增加了。 1)对称近邻平滑滤波器:从模板中的对称点对中寻找与待处理的像素相同区域的点,然后对选出的点做均值运算。 2)最小方差平滑滤波器:将属于通过一个区域的可能的相邻关系以9种模板表示出来,然后计算每个模板中的灰度分布方差,以方差最小的那个模板的均值替代原像素值。 3)sigma拼花滤波器:根据统计学的原理,属于同一类别的元素的置信区间,落在均值附件+-2δ范围内:Sigma滤波器是构造一个模板,计算模板的标准差δ,置信区间为当前像素值的+-2δ范围。将模板中落在置信范围内的像素的均值替换原来的像素值。 9,高斯滤波器: 1)介绍:高斯模糊:也叫高斯平滑:通常用来减少图像噪声以及降低细节层次。 2)原理:周围像素的平均值,所谓的模糊:可以理解为每一个像素都去周边像素的平均值。在计算平均值时,取值范围越大,模糊效果越强烈。从数值上看,数值越平滑,相当于图像的模糊半径越大,图像越模糊。 3)如果使用简单的平均,由于图形是连续的,越靠近的点的关系越密切,越远离的点关系越疏远,因此,加权平均更合理。距离越近的点权重越大,距离越远的点权重越小。 4)正态分布的权重:在图形上,正态分布式一种钟形的曲线,越接近中心,取值越大,越远离中心,取值越小。计算平均值的时候,只需要将中心点作为原点,其他点按照其在正太分布上的位置,分配权重,就可以得到一个加权平均值。 其中的u是x的均值,其中的δ是x的方差,因为在计算平均值的时候,中心店说就是原点,所以u等于0,更具一维的高斯函数,可以导出二维高斯函数。, 有了这个函数,就可以计算每个点的权重了。 6)为了计算权重矩阵,需要设定δ的值,之后求出权重矩阵,根据高斯函数求得。因为权重的和等于1,因此获得的值分别除以权重和,得到最终的权重矩阵。 7)高斯滤波器是一类根据高斯函数的形状来选择权值的线性的平滑滤波器,高斯平滑滤波器对于抑制服从正态分布的噪声非常有效,一维零均值高斯函数为: g(x)=exp( -x^2/(2 sigma^2),其中,高斯分布参数sigma决定了高斯函数的宽度,对于图形处理来说,常用二维零均值离散高斯函数作为平滑滤波器。 高斯函数由五个重要的性质;这些性质表明:高斯平滑滤波器无论在空间域还是在频率域都是十分有效的的低通滤波器。、 a,二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的,一般来说,一幅图像的边缘方向上是不知道的,因此滤波前是无法确定一个方向上比另一个方向上需要更多的平滑,旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任何一方。 b,高斯函数是单值函数,这表明:高斯滤波用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点的权值是随该点用户中心店的距离单调增减的,因为边缘是一种图像局部特征,吐过平滑运算对离算子中心很远的像素点仍然有很大的作用,则平滑运算很是图像失真。 c,高斯函数的傅里叶变化频谱是单瓣的,这一性质是高斯函数傅里叶变换等于高斯函数本身;图像常备不希望的高斯信号多污染(噪声和细纹理),而所希望的图形特征(如边缘),既含有低频分量,又含有高频分量。高斯函数傅里叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染。同时保留了大部分所需的信号。, d,高斯滤波器宽度(决定这平滑程度,)是由参数δ表征的,而且δ和平滑程度的关系是非常简单的,δ越大,高斯滤波器的频带就越宽,平滑程度就越好,通过调节平滑程度参数δ,可在图像特征过分模糊与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量之间取得折中。 e,由于高斯函数的可分离性,较大尺寸的高斯滤波器可得以有效的实现,二维高斯函数卷积可以分两步来进行,首先将图像与一维高斯函数进行卷积,然后将卷积结果与方向垂直的相同的一维高斯函数卷积,因此,二维高斯滤波的计算量随滤波模板宽度成线性增长而不是平方增长。 高斯图像滤波: 1,图像滤波总体上讲包括空域滤波和频域滤波,频域滤波需要先进行傅里叶变换值频域处理然后在反变换回空间域还原图像,空域滤波是直接对图形的数据做空间变换达到滤波的目的,它是一种邻域运算,即输出图像中任何像素的值都是通过采用一定的算法,根据输入图像中对用像素周围一定邻域内像素的值得来的,如果输出像素是输入像素邻域像素的线性组合则称为线性滤波。(最常见是均值滤波和高斯滤波),否则为非线性滤波(中值滤波,边缘保持滤波等)。 2,线性平滑滤波去除高斯噪声的效果很好,且在大多数的情况下,对其他类的噪声也有很好的效果,线性滤波器使用灵虚窗函数内像素加权和来实现滤波,特别典型的是:同一模式的权重因子可以作用在每一个窗口中,也就是线性滤波器是空间不变的,这样就可以使用卷积模板来实现滤波。如果图像的不同部分使用不同的滤波权重因子,且仍可以用滤波器完成加权运算,因此线性滤波器是空间可变的。任何不适像素加权运算的滤波器都属于非线性滤波器。非线性滤波器也可以是空间不变的。 10,均值滤波器: 1)定义:对当前处理的像素,选择衣蛾模板,该模板为器邻近的若干个像素组成,用模板的均值来替代原像素的方法, 方法的优缺点:1)算法简单,计算速度快; 2)缺点:降低噪声的同时,是图像产生模糊,特别是景物的边缘和细节部分。 3)均值滤波器是图像处理中一种常见的滤波器,它主要用于平滑噪声,主要是利用某像素点周边的像素的平均值来达到平滑噪声的效果。 4)均值滤波对所有的点都是同等对待,在将噪声分摊的同时,将景物的边界点也分摊了。为了改善效果,就可采用加权平均的方式来构造滤波器。 5)对于高斯噪声(因为图像找给你的每点都是污染点,所以中值滤波选不到合适的干净的点),均值滤波要比中值滤波效果好。椒盐噪声:中值滤波比均值要好。