统计概率模型-高斯判别分析

统计概率模型

1、高斯判别分析

2、朴素贝叶斯

3、隐马尔可夫模型

4、最大熵马尔科夫模型

5，条件随机场

6，马尔科夫决策过程

一、高斯判别分析

一、生成模型

​ 机器学习模型有一种分类方式：判别模型和生成模型。它们之前的区别在于判别模型是直接从数据特征到标签，而生成模型是从标签到数据特征。形式化的表示就是是否使用了贝叶斯公式：

maxP(Y|X)=P(X|Y)P(Y)P(X)→maxP(X|Y)P(Y) max P ( Y | X ) = P ( X | Y ) P ( Y ) P ( X ) → max P ( X | Y ) P ( Y )

机器学习模型从概率的角度来看就是最大 P(Y|X) P ( Y | X ) 的条件概率，判别模型的思想是直接最大化这个概率（Fisher线性判别，线性感知机），生成模型则是通过贝叶斯模型最大后验概率 P(X|Y)P(Y) P ( X | Y ) P ( Y ) ，其中 P(X|Y) P ( X | Y ) 可以看作是从标签d生成数据， P(Y) P ( Y ) 则是标签的先验概率。

​ 基本上从标签到数据的模型都是基于对样本的统计，以下的模型都是基于数据的统计（但不全是生成模型），所以笔者将这部分归类到统计概率模型。

二、高斯判别分析

​ 高斯判别分析是一个典型的生成模型，其假设 P(X|Y) P ( X | Y ) 服从一个高斯分布， P(Y) P ( Y ) 服从一个伯努利分布通过统计样本来确定高斯分布和伯努利分布的参数，进而通过最大后验概率来进行分类。

假设数据在标签为 Y Y 下，特征为 X X 的条件概率为 P(X|Y) P ( X | Y ) 服从多元高斯分布 X−N(μ,Σ) X − N ( μ , Σ ) ，其中 μ μ 为均值， Σ Σ 为协方差矩阵。则有：

P(X|Y)=12πn2|Σ|12exp(−12(x−μ)TΣ−1(x−μ)) P ( X | Y ) = 1 2 π n 2 | Σ | 1 2 e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) )

而先验分布 P(Y) P ( Y ) 服从伯努利分布 y∼Bernoulli(ϕ) y ∼ B e r n o u l l i ( ϕ ) ，当 y∈(0,1) y ∈ ( 0 , 1 ) 时，是一元伯努利分布，当 y∈(1，2,...k) y ∈ ( 1 ， 2 , . . . k ) 时，同样可以像Logistic推广到SoftMax一样处理多元伯努利分布。下面以一元伯努利分布为例计算完整的高斯判别模型的概率：

y∼Bernoulli(ϕ)(x|y=0)∼N(μ0,Σ0)(x|y=1)∼N(μ1,Σ1) y ∼ B e r n o u l l i ( ϕ ) ( x | y = 0 ) ∼ N ( μ 0 , Σ 0 ) ( x | y = 1 ) ∼ N ( μ 1 , Σ 1 )

p(y)=ϕy(1−ϕ)1−yp(x|y=0)=12πn2|Σ|12exp(−12(x−μ0)TΣ−10(x−μ0))p(x|y=0)=12πn2|Σ|12exp(−12(x−μ1)TΣ−11(x−μ1)) p ( y ) = ϕ y ( 1 − ϕ ) 1 − y p ( x | y = 0 ) = 1 2 π n 2 | Σ | 1 2 e x p ( − 1 2 ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) ) p ( x | y = 0 ) = 1 2 π n 2 | Σ | 1 2 e x p ( − 1 2 ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) )

最大化后验概率即为：

argmaxyP(y|x)=p(x|y)p(y)p(x)→argmaxyp(x|y)p(y) a r g max y P ( y | x ) = p ( x | y ) p ( y ) p ( x ) → a r g max y p ( x | y ) p ( y )

极大似然函数有：

maxL(ϕ,μ0,μ1,Σ0,Σ1)=∏i=1mp(x(i),y(i);ϕ,μ0,μ1,Σ0,Σ1)⇔log∏i=1mp(x(i),y(i);ϕ,μ0,μ1,Σ0,Σ1) max L ( ϕ , μ 0 , μ 1 , Σ 0 , Σ 1 ) = ∏ i = 1 m p ( x ( i ) , y ( i ) ; ϕ , μ 0 , μ 1 , Σ 0 , Σ 1 ) ⇔ l o g ∏ i = 1 m p ( x ( i ) , y ( i ) ; ϕ , μ 0 , μ 1 , Σ 0 , Σ 1 )

最大似然估计得到参数如下：

ϕ=1m∑i=1m1(y(i)=1)μ0=∑mi=11(y(i)=0)x(i)∑mi=11(y(i)=0)μ1=∑mi=11(y(i)=1)x(i)∑mi=11(y(i)=1)Σ=∑i=1m(x(i)−μy(i))(x(i)−μy(i))T ϕ = 1 m ∑ i = 1 m 1 ( y ( i ) = 1 ) μ 0 = ∑ i = 1 m 1 ( y ( i ) = 0 ) x ( i ) ∑ i = 1 m 1 ( y ( i ) = 0 ) μ 1 = ∑ i = 1 m 1 ( y ( i ) = 1 ) x ( i ) ∑ i = 1 m 1 ( y ( i ) = 1 ) Σ = ∑ i = 1 m ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T

其中 1(y(i)=1) 1 ( y ( i ) = 1 ) 为指示函数，同时假设 Σ0=Σ1=Σ Σ 0 = Σ 1 = Σ ， Σ Σ 反映一类数据分布的方差，可以看出最大似然估计的参数值就是基于对样本的一个统计。

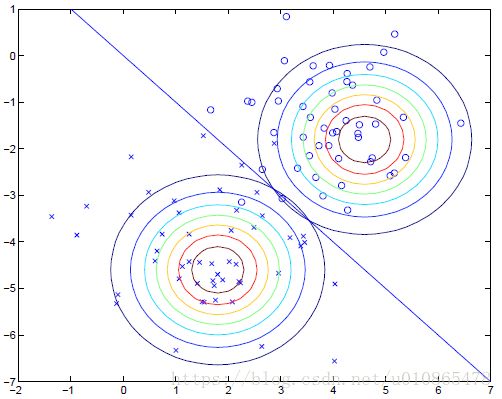
下图为一个简单的高斯判别模型示意图：

从上图可以看出，高斯判别模型通过建立两类样本的特征模型，对于二分类问题，然后通过比较后验概率的大小来得到一个分类边界。

回过头来再看最小错误贝叶斯决策（Logistic回归）与一维高斯判别模型，有趣的是最后得到的决策函数也类似于sigmoid函数。

高斯判别模型与Logistic回归比较

​ 高斯判别模型的假设是 P(X|Y) P ( X | Y ) 服从一个高斯分布， P(Y) P ( Y ) 服从一个伯努利分布

​ Logistic回归的概率解释中可以看出它的假设是 P(Y|X,θ) P ( Y | X , θ ) 服从伯努利分布

​ 由高斯判别分析模型可以得到，加上一些推导可以得到，反之不然：

p(y=1|x;ϕ,μ0,μ1,Σ)=11+e−θTx p ( y = 1 | x ; ϕ , μ 0 , μ 1 , Σ ) = 1 1 + e − θ T x

其中， θ θ 是参数 ϕ，μ0,μ1,Σ ϕ ， μ 0 , μ 1 , Σ 的某种函数。也就是说高斯判别模型是Logistic回归模型中的一种特例。

​ 这里我们可以发现高斯判别模型的假设强于Logistic模型，也就是说Logistic回归模型的鲁棒性更强。这就表示在数据量足够大时，跟倾向于选择Logistic回归模型。而在数据量较小，且 P(X|Y) P ( X | Y ) 服从一个高斯分布非常合理时，选择高斯判别分析模型更适合。