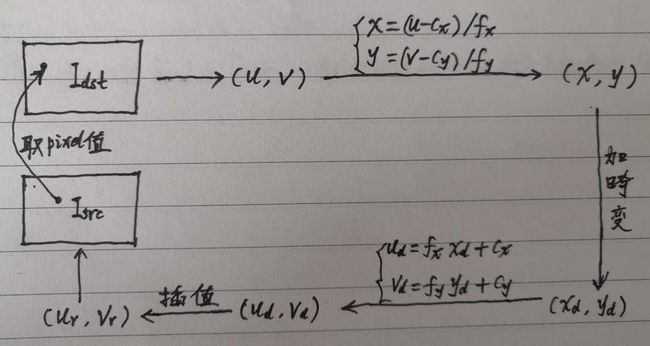针孔相机投影模型以及畸变模型

世界坐标系 到 像素坐标系

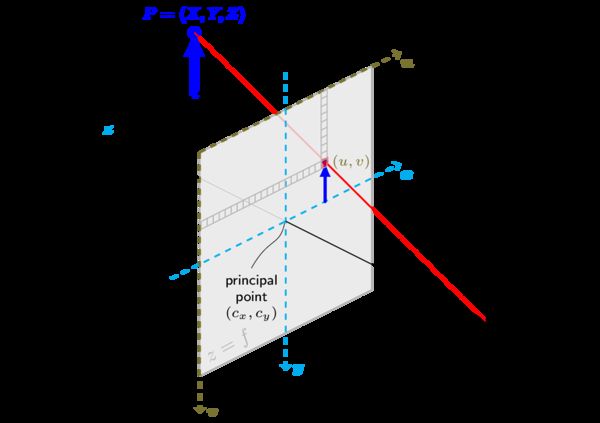
世界坐标系中三维点$M=[X,Y,Z{]}^T$ 和 像素坐标系中二维点$m=[u,v{]}^T$的关系为：
$$s\tilde{m}=A[Rt]\tilde{M}$$
即（针孔相机模型）
$$\begin{array}{r}s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\end{array}$$
其中，$s$为缩放因子，$A$为相机的内参矩阵，$[Rt]$为相机的外参矩阵，$\tilde{m}$和$\tilde{M}$分别为$m$和$M$对应的齐次坐标。

针孔相机模型 (pinhole)

相机将三维世界中的坐标点（单位：米）映射到二维图像平面（单位：像素）的过程能够用一个几何模型来描述，其中最简单的称为针孔相机模型 (pinhole camera model)，其框架如下图所示。

世界坐标系 到 相机坐标系

$$\begin{array}{r}\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=R\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+t=[Rt]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\end{array}$$

相机坐标系 到 像素坐标系

根据三角形相似关系，有
$$\frac{Z_c}{f}=\frac{X_c}{x}=\frac{Y_c}{y}$$
整理，得
$$\{\begin{array}{l}x=f\cdot \frac{X_c}{Z_c}\\ y=f\cdot \frac{Y_c}{Z_c}\end{array}$$
像素坐标系和成像平面坐标系之间，相差一个缩放和平移，联合上式整理得

$$\{\begin{array}{l}u=\alpha \cdot x+c_x\\ v=\beta \cdot y+c_y\end{array}⟹\{\begin{array}{l}u=\alpha f\cdot \frac{X_c}{Z_c}+c_x\\ v=\beta f\cdot \frac{Y_c}{Z_c}+c_y\end{array}$$

或

$$\{\begin{array}{l}u=\frac{1}{dx}\cdot x+c_x\\ v=\frac{1}{dy}\cdot y+c_y\end{array}⟹\{\begin{array}{l}u=\frac{f}{dx}\cdot \frac{X_c}{Z_c}+c_x\\ v=\frac{f}{dy}\cdot \frac{Y_c}{Z_c}+c_y\end{array}$$

其中，

$$\{\begin{array}{l}dx=\frac{W_{sensor}}{W_{image}}\\ dy=\frac{H_{sensor}}{H_{image}}\end{array}$$

则

$$\{\begin{array}{l}{f}_x=\frac{f}{dx}\\ f_y=\frac{f}{dy}\end{array}⟹\{\begin{array}{l}u=f_x\frac{X_c}{Z_c}+c_x\\ v=f_y\frac{Y_c}{Z_c}+c_y\end{array}$$

或

$$\{\begin{array}{l}{f}_{nx}=\frac{f}{W_{sensor}}\\ f_{ny}=\frac{f}{H_{sensor}}\end{array}⟹\{\begin{array}{l}u=f_{nx}{W}_{image}\frac{X_c}{Z_c}+c_x\\ v=f_{ny}{H}_{image}\frac{Y_c}{Z_c}+c_y\end{array}$$

其中，

• $f$为镜头焦距，单位为米;
• $\alpha$、$\beta$的单位为像素/米;
• $dx$、$dy$为传感器x轴和y轴上单位像素的尺寸大小，单位为米/像素;
• $f_x$、$f_y$为x、y方向的焦距，单位为像素;
• $f_{normal\_x}$、$f_{normal\_y}$为x、y方向的归一化焦距;
• $(c_x,c_y)$为主点，图像的中心，单位为像素。

最终，写成矩阵的形式为：
$$\begin{array}{r}\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{Z_c}\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]\end{array}$$
或
$$\begin{array}{r}{Z}_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]\end{array}$$

畸变模型

多项式畸变模型 (radial-tangential)

透镜的畸变主要分为径向畸变和切向畸变。

径向畸变是由于透镜形状的制造工艺导致，且越向透镜边缘移动径向畸变越严重，实际情况中我们常用r=0处的泰勒级数展开的前几项来近似描述径向畸变，径向畸变后的归一化坐标为：

$$\{\begin{array}{l}{x}_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)\\ y_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)\end{array}$$

切向畸变是由于透镜和CMOS或者CCD的安装位置误差导致，切向畸变需要两个额外的畸变参数来描述，切向畸变后的归一化坐标为：

$$\{\begin{array}{l}{x}_{distorted}=x+2p_{1}xy+p_2(r^2+2x^2)\\ y_{distorted}=y+2p_{2}xy+p_1(r^2+2y^2)\end{array}$$

联合上式，整理得

$$\{\begin{array}{l}{x}_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{1}xy+p_2(r^2+2x^2)\\ y_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{2}xy+p_1(r^2+2y^2)\end{array}$$

其中，$r^2=x^2+y^2$

综上，我们一共需要5个畸变参数$(k_1,k_2,k_3,p_1,p_2)$来描述透镜畸变。

畸变矫正

• [图像]畸变校正详解

• 核心示例代码 (from here)

  for (int v = 0; v < height; v++) {
    for (int u = 0; u < width; u++) {
  
      double u_distorted = 0, v_distorted = 0;
  
      double x = (u-cx)/fx;
      double y = (v-cy)/fy;
  
      double x2 = x*x, y2 = y*y, xy = x*y, r2 = x2 + y2;
      double x_radial = x * (1 + k1*r2 + k2*r2*r2);
      double y_radial = y * (1 + k1*r2 + k2*r2*r2);
      double x_tangential = 2*p1*xy + p2*(r2 + 2*x2);
      double y_tangential = 2*p2*xy + p1*(r2 + 2*y2);
      double xd = x_radial + x_tangential;
      double yd = y_radial + y_tangential;
  
      u_distorted = xd*fx + cx;
      v_distorted = yd*fy + cy;
  
      // 最近邻插值
      if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < width && v_distorted < height)
          img_dst(v, u) = (*this)((int) v_distorted, (int) u_distorted);
      else
          img_dst(v, u) = 0;
    }
  }