Python3:《机器学习实战》之支持向量机(2)简化版SMO
Python3:《机器学习实战》之支持向量机(2)简化版SMO
- 转载请注明作者和出处:http://blog.csdn.net/u011475210
- 代码地址:https://github.com/WordZzzz/ML/tree/master/Ch06
- 操作系统:WINDOWS 10
- 软件版本:python-3.6.2-amd64
- 编 者:WordZzzz
- Python3机器学习实战之支持向量机2简化版SMO
- 前言
- Platt的SMO算法
- 应用简化版SMO算法处理小规模数据集
前言
SVM有很多实现,但我们只关注其中最流行的一种实现,即序列最小优化( Sequential MInimal Optimization,SMO )算法。
下面我们就开始讨论SMO算法,本篇博文先给出一个简化的版本,以便我们能够正确理解它的工作流程。
Platt的SMO算法
1996年,伟大的John Platt发布了一个称为SMO的强大算法,用于训练SVM。Platt的SMO算法是将大优化问题分解为多个小优化问题来求解的。这些小优化问题往往很容易求解,并且对它们进行顺序来求解的结果与将他们作为整体来求解的结果是完全一致的,但是求解时间却大大缩短。
SMO算法的目标是求出一系列alpha和b,一旦求出了这些alpha,就很容易计算出权重向量w并得到分隔超平面。
SMO的工作原理是:每次循环中选择两个alpha进行优化处理。一旦找到一对合适的alpha,那么就增大其中一个同时减小另一个。这里所谓的“合适”就是指两个alpha必须要符合一定的条件,条件之一就是这两个alpha必须要在间隔边界之外,另一个条件则是这两个alpha还没有进行过区间化处理或者不在边界上。
应用简化版SMO算法处理小规模数据集
Platt SMO算法中的外循环确定要优化的最佳alpha对。而简化版会跳过这一部分,首先在数据集上遍历每一个alpha,然后在剩下的alpha集合中随机选择另一个alpha来构成alpha对。这里有一点相当重要,就是我们要同时改变两个alpha,因为我们需要满足一个约束条件:
$$
\sum \alpha_i · label^{(i)} = 0
$$由于改变一个alpha可能会导致该约束条件失效,因为需要同时改变两个alpha,一增一减,改变的量相同。
在实现简化版SMO之前,我们需要先构造几个辅助函数。打开文本编辑器,将下面的代码加入svmMLiA.py中。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date : 2017-09-21 21:02:51
# @Author : WordZzzz ([email protected])
# @Link : http://blog.csdn.net/u011475210
from numpy import *
from time import sleep
def loadDataSet(fileName):
"""
Function: 加载数据集
Input: fileName:数据集
Output: dataMat:数据矩阵
labelMat:类别标签矩阵
"""
#初始化数据列表
dataMat = []
#初始化标签列表
labelMat = []
#打开文件
fr = open(fileName)
#遍历每一行数据,读取数据和标签
for line in fr.readlines():
#strip删除头尾空白字符,然后再进行分割
lineArr = line.strip().split('\t')
#填充数据集
dataMat.append([float(lineArr[0]), float(lineArr[1])])
#填充类别标签
labelMat.append(float(lineArr[2]))
#返回数据集和标签列表
return dataMat, labelMat
def selectJrand(i, m):
"""
Function: 随机选择
Input: i:alpha下标
m:alpha数目
Output: j:随机选择的alpha下标
"""
#初始化下标j
j = i
#随机化产生j,直到不等于i
while (j == i):
j = int(random.uniform(0,m))
#返回j的值
return j
def clipAlpha(aj, H, L):
"""
Function: 设定alpha阈值
Input: aj:alpha的值
H:alpha的最大值
L:alpha的最小值
Output: aj:处理后的alpha的值
"""
#如果输入alpha的值大于最大值,则令aj=H
if aj > H:
aj = H
#如果输入alpha的值小于最小值,则令aj=L
if L > aj:
aj = L
#返回处理后的alpha的值
return aj首先是我们熟悉的老哥loadDataSet(),用来打开文件并对其进行解析,从而得到每行的类别标签和整个数据矩阵;然后是selectJrand(),用来随机选择第二个alpha的下标(只要和第一个alpha下标不一样就行);最后一个是clipAlpha()函数,用于设定阈值,限制alpha的值。
>>> reload(svmMLiA)
'svmMLiA' from 'E:\\机器学习实战\\mycode\\Ch06\\svmMLiA.py'>
>>> dataArr, labelArr = svmMLiA.loadDataSet('testSet.txt')
>>> labelArr
[-1.0, -1.0, 1.0, -1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, 1.0, -1.0, 1.0, 1.0, -1.0, 1.0, -1.0, -1.0, -1.0, 1.0, -1.0, -1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, 1.0, 1.0, 1.0, -1.0, 1.0, -1.0, -1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, 1.0, 1.0, 1.0, 1.0, -1.0, 1.0, 1.0, -1.0, -1.0, 1.0, 1.0, -1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, -1.0, 1.0, -1.0, -1.0, 1.0, 1.0, 1.0, -1.0, 1.0, 1.0, -1.0, -1.0, 1.0, -1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, -1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0]
>>> 简化版SMO伪代码:
创建一个alpha向量并将其初始化为0向量
当迭代次数小于最大迭代次数时(外循环):
对数据集中的每个数据向量(内循环):
如果该数据向量可以被优化:
随机选择另外一个数据向量
同时优化这两个向量
如果两个向量都不能被优化,退出内循环
如果所有向量都没被优化,则增加迭代数目,继续下一次循环下述代码是SMO算法中的一个有效版本,如果看不懂,可以先找SVM的公式推导看看。打开文本编辑器,将下面的代码加入svmMLiA.py中。
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
"""
Function: 简化版SMO算法
Input: dataMatIn:数据集
classLabels:类别标签
C:常数C
toler:容错率
maxIter:最大的循环次数
Output: b:常数项
alphas:数据向量
"""
#将输入的数据集和类别标签转换为NumPy矩阵
dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
#初始化常数项b,初始化行列数m、n
b = 0; m,n = shape(dataMatrix)
#初始化alphas数据向量为0向量
alphas = mat(zeros((m,1)))
#初始化iter变量,存储的是在没有任何alpha改变的情况下遍历数据集的次数
iter = 0
#外循环,当迭代次数小于maxIter时执行
while (iter < maxIter):
#alpha改变标志位每次都要初始化为0
alphaPairsChanged = 0
#内循环,遍历所有数据集
for i in range(m):
#multiply将alphas和labelMat进行矩阵相乘,求出法向量w(m,1),w`(1,m)
#dataMatrix * dataMatrix[i,:].T,求出输入向量x(m,1)
#整个对应输出公式f(x)=w`x + b
fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i,:].T)) + b
#计算误差
Ei = fXi - float(labelMat[i])
#如果标签与误差相乘之后在容错范围之外,且超过各自对应的常数值,则进行优化
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
#随机化选择另一个数据向量
j = selectJrand(i, m)
#对此向量进行同样的计算
fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j,:].T)) + b
#计算误差
Ej = fXj - float(labelMat[j])
#利用copy存储刚才的计算值,便于后期比较
alphaIold = alphas[i].copy(); alpahJold = alphas[j].copy()
#保证alpha在0和C之间
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
#如果界限值相同,则不做处理直接跳出本次循环
if L == H: print("L == H"); continue
#最优修改量,求两个向量的内积(核函数)
eta = 2.0 * dataMatrix[i,:] * dataMatrix[j,:].T - dataMatrix[i,:] * dataMatrix[i,:].T - dataMatrix[j,:] * dataMatrix[j,:].T
#如果最优修改量大于0,则不做处理直接跳出本次循环,这里对真实SMO做了简化处理
if eta >= 0: print("eta >= 0"); continue
#计算新的alphas[j]的值
alphas[j] -= labelMat[j] * (Ei - Ej) / eta
#对新的alphas[j]进行阈值处理
alphas[j] = clipAlpha(alphas[j], H, L)
#如果新旧值差很小,则不做处理跳出本次循环
if (abs(alphas[j] - alpahJold) < 0.00001): print("j not moving enough"); continue
#对i进行修改,修改量相同,但是方向相反
alphas[i] += labelMat[j] * labelMat[i] * (alpahJold - alphas[j])
#新的常数项
b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i,:] * dataMatrix[i,:].T - labelMat[i] * (alphas[j] - alpahJold) * dataMatrix[i,:] * dataMatrix[j,:].T
b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i,:] * dataMatrix[j,:].T - labelMat[j] * (alphas[j] - alpahJold) * dataMatrix[j,:] * dataMatrix[j,:].T
#谁在0到C之间,就听谁的,否则就取平均值
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2) / 2.0
#标志位加1
alphaPairsChanged += 1
#输出迭代次数,alphas的标号以及标志位的值
print("iter: %d i: %d, pairs changed %d" % (iter, i, alphaPairsChanged))
#如果标志位没变,即没有进行优化,那么迭代值加1
if (alphaPairsChanged == 0): iter += 1
#否则迭代值为0
else: iter = 0
#打印迭代次数
print("iteration number: %d" % iter)
#返回常数项和alphas的数据向量
return b, alphas运行结果如下:
>>> reload(svmMLiA)
'svmMLiA' from 'E:\\机器学习实战\\mycode\\Ch06\\svmMLiA.py'>
>>> b, alphas = svmMLiA.smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
iter: 0 i: 0, pairs changed 1
j not moving enough
j not moving enough
iter: 0 i: 5, pairs changed 2
j not moving enough
j not moving enough
iter: 0 i: 17, pairs changed 3
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
iter: 0 i: 54, pairs changed 4
j not moving enough
j not moving enough
L == H
j not moving enough
L == H
j not moving enough
iteration number: 0
j not moving enough
iter: 0 i: 5, pairs changed 1
···
···
iteration number: 0
j not moving enough
j not moving enough
j not moving enough
iteration number: 1
j not moving enough
j not moving enough
j not moving enough
···
···
j not moving enough
j not moving enough
j not moving enough
iteration number: 39
j not moving enough
j not moving enough
j not moving enough
iteration number: 40 上述过程可能需要几分钟才会收敛,一旦运行结束,我们就可以对结果进行查看:
>>> b
matrix([[-3.87260031]])
>>> alphas[alphas > 0]
matrix([[ 0.10195497, 0.25933768, 0.0240785 , 0.33721415]])
>>> from numpy import *
>>> shape(alphas[alphas > 0])
(1, 4)
>>> for i in range(100):
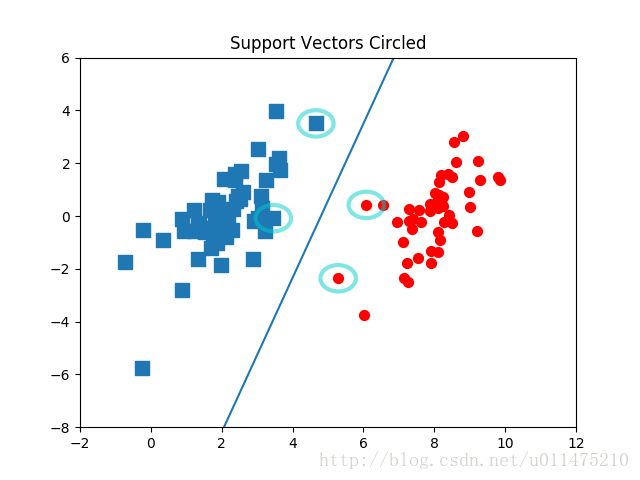
... if alphas[i] > 0.0: print(dataArr[i], labelArr[i])
...
[4.658191, 3.507396] -1.0
[3.457096, -0.082216] -1.0
[5.286862, -2.358286] 1.0
[6.080573, 0.418886] 1.0
>>> 由于SMO算法的随机性,每次运行之后得到的结果不尽相同。alphas[alphas > 0]命令是数组过滤的一个实例,得到仅仅包含大于0的值的矩阵,而且它只对NumPy类型有用,却并不适用于Python中的正则表。
我们在数据集上把这些支持向量画出来:
希望通过本篇博文,大家对SMO的工作流程有了一定得了解,至于完成版的SMO,WordZzzz将会在下一篇博文介绍给大家。
系列教程持续发布中,欢迎订阅、关注、收藏、评论、点赞哦~~( ̄▽ ̄~)~
完的汪(∪。∪)。。。zzz