论文研读-基于决策变量分析的大规模多目标进化算法

论文研读-基于决策变量分析的大规模多目标进化算法

Multiobjective Evolutionary Algorithm Based on Decision Variable Analyses for Multiobjective Optimization Problems With Large-Scale Variables

觉得有用的话,欢迎一起讨论相互学习~

• 此篇文章为 X. Ma et al., "A Multiobjective Evolutionary Algorithm Based on Decision Variable Analyses for Multiobjective Optimization Problems With Large-Scale Variables," in IEEE Transactions on Evolutionary Computation, vol. 20, no. 2, pp. 275-298, April 2016, doi: 10.1109/TEVC.2015.2455812. 的论文学习笔记，只供学习使用，不作商业用途，侵权删除。并且本人学术功底有限如果有思路不正确的地方欢迎批评指正！

Abstract

• 最新的多目标进化算法（MOEA）将所有决策变量作为一个整体来处理(即所有决策变量不做区别，或者同时对所有维度的决策变量进行优化)以优化性能。受单目标优化领域中协作协同进化和链接学习方法的启发，将一个困难的高维问题分解为一组更易于解决的较简单和低维的子问题十分具有意义。但是，由于没有关于目标函数的先验知识，因此不清楚如何分解目标函数。此外，使用这样的分解方法来解决多目标优化问题（MOP）十分困难，因为它们的目标函数通常相互冲突。也就是说，仅仅改变决策变量将产生非支配的解决方案。本文提出了相互依赖变量分析和控制变量分析，以解决上述两个困难。因此，本文提出了一种基于决策变量分析（DVA）的MOEA。并使用控制变量分析用于识别目标函数之间的冲突。更具体地说，哪些变量影响生成的解的多样性，哪些变量在总体收敛中起重要作用。基于链接学习的方法，相互依赖变量分析将决策变量分解为一组低维子组件。实证研究表明，DVA可以提高大多数困难MOP的解决方案质量。

关键词

• Cooperative coevolution, decision variable analysis (DVA), interacting variables, multiobjective optimization, problem decomposition. 合作协同进化，决策变量分析 （DVA），交叉变量，多目标优化，问题分解。

Introduction

• 具有一次运行即可生成许多代表性近似解的优势，进化算法（EA）已广泛用于多目标优化问题（MOP）[1]。当前，最先进的多目标EA（MOEA）[2]-[4]更加注意保持目标空间中获得的解决方案的多样性，并将所有决策变量作为一个整体(即所有决策变量不做区别，或者同时对所有维度的决策变量进行优化)进行优化。由于MOP的复杂性和难度，简化一个较为困难的MOP的方法很有研究价值。影响优化问题复杂性和难度的主要因素是决策变量的数量[5]。受协作协同进化[6] – [9]和链接学习方法[10]，[11]的启发，一种理想的方式是将具有高维变量的MOP的每个目标函数分解为许多更简单和低维的子函数。如果存在这种分解，则优化原始函数等于分别解决每个子函数。上述“分而治之”策略的主要困难是如何选择良好的分解方法，以使不同子函数之间的相互依赖性保持最小。尽管分解对协作协同进化和链接学习算法的性能具有重要影响，但是通常对于给定问题的隐藏结构了解不足，无法帮助算法设计者发现合适的分解。因此，有必要设计一种算法，该算法可以检测决策变量之间的相互作用以划分决策变量。为此，开发了相互依赖变量分析。
• 使用在单目标优化问题（SOP）中提出的分而治之策略用于解决MOP并非易事，因为MOP的目标函数相互冲突。 目标函数之间的冲突在这里指的是通过更改决策变量来生成的无法比较的解决方案。 冲突意味着MOP的目标是找到一组Pareto最优解，而不是像SOP中那样找到单个最优解。 由于位置变量和混合变量[12]对生成的解的传播有影响，因此两种变量都被视为目标函数之间冲突的根源。
• 基于上述决策变量的控制分析和两个变量之间的相互依赖分析，我们提出了基于决策变量分析的MOEA（MOEA / DVA）。 基于决策变量的控制分析，MOEA / DVA将复杂的MOP分解为一组更简单的子MOP。 基于两个变量之间的相互依赖性分析，决策变量被分解为几个低维子组件。 每个子MOP都会一个一个地独立优化子组件。 因此，与大多数优化了所有决策变量的MOEA相比，MOEA / DVA有望具有优势。
• 论文主要贡献如下所示：

1. 为了帮助读者理解变量相互依赖的概念，提供了两个必要条件。
2. 为了学习目标函数之间的冲突，使用了位置变量和混合变量[12]的概念。 此外，基于位置变量和混合变量而不是权重向量，本文提供了一种新的分解方案，可将困难的MOP转换为一组更简单的子MOP。
3. 在具有良好的相互作用变量理论基础的情况下，本文尝试将具有高维变量的困难MOP分解为一组具有低维子组件的简单子MOP。
4. 本文证明了连续ZDT和DTLZ问题的目标函数是可分离的函数。对于2009年IEEE进化计算大会（CEC）竞赛的无约束多目标目标函数（UF）问题[13]证明了其两个决策变量之间的相互作用是稀疏的，并且集中在混合变量上。

• 本文的其余部分安排如下。 第二部分介绍了有关多目标优化的定义和表示，变量链接，决策变量的控制属性，决策变量的链接学习技术以及基于学习链接的变量划分技术的几种相关背景。 第三节介绍了DVA和提出的算法MOEA / DVA。 第四节说明并分析了实验结果。 第五节总结了本文。

相关工作

• 本节介绍相关研究背景的两个方面。 一个是SOP(单目标优化问题)。 SOP的相关研究背景包括决策变量的可分离性和不可分离性，各种链接学习方法以及基于学习链接的决策变量的不同划分方法。 另一个是MOP（多目标优化问题）。 MOP的相关研究背景包括MOP的定义和符号，连续MOP的规律性[14]以及决策变量的控制性。

可分离和不可分离决策变量

• f(x)只有当每一个决策变量都能够被单独地进行优化才叫做可分离函数。
  

• 定义1 表示可以通过逐一优化变量来解决可分离函数。 可分离性意味着每个变量都独立于任何其他变量。 关于可分离函数和不可分离函数的其他定义可以在[7]和[12]中找到。 球面函数sphere function，广义Rastrigin函数，广义Griewank函数和Ackley函数[15]，[16]是可分离函数的代表。 基本上，可分离性函数意味着可以独立于任何其他变量来优化问题中涉及的决策变量，而不可分离性函数意味着至少两个决策变量之间存在相互作用interactions。

• 变量依赖性是问题的重要方面，它们描述了问题的结构。如果预先知道问题的变量依赖性，则很容易将决策变量划分为几个子组件。因此，通过分别优化具有低维子组件的几个较简单的子问题来解决高维变量的难题是十分有益的。但是，问题的变量依赖性通常是事先未知的。此外，“相互依存变量”的定义不是唯一的。 Yu等[17]提出，当且仅当没有两个决策变量所携带的信息，关联子问题不能被优化时，两个决策变量相互作用。 Weise等[5]提出，如果改变一个决策变量对适应度的影响依赖于另一个决策变量的值，则两个决策变量会相互影响。与以上两个定性定义不同，本文使用以下相互依赖变量的定量定义。

• 定义2 ：
  

• 定义2可以从Yang等人[7]提出的不可分函数的定义中得出。在这些“相互依赖变量”的不同定义中，我们选择“定义2”作为相互依赖变量的定义 因为该定义是 定量的 且易于使用。

• 对于一个不可分的函数f(x),如果 任意两个不同的决策变量xi,xj相互作用，则称这个函数是完全不可分的 Schwefel’s function 2.22, generalized Griewank function, and Ackley’s function [15], [16] 是完全不可分的函数 这里我有一点不懂，上一段中说广义Griewank函数和Ackley函数是可分离的函数呀，为什么这里又表述为完全不可分的呢？ . 在完全可分和完全不可分的函数之间，存在大量的部分可分函数[16],[19]. 如果最多k个决策变量x不独立,就说一个函数是k-不可分的。 通常，不可分程度越大，函数求解越难[5]。 实际的优化问题很可能由几个独立的模块组成[16]，[19]。 这些问题大多都是部分可分离函数。 对于此类问题，有趣的一点是，具有高维决策变量的困难函数可以分解为具有低维子组件的几个简单子函数。 因此，部分可分离的函数在优化[20]和进化计算[16]，[21]领域引起了很多关注。

决策变量的内部依赖检测技术

• 对于具有模块化特征的问题，如果算法能够学习问题结构并相应地分解函数，则解决问题的难度将迅速降低[22]。 因此，降低问题难度的关键问题是检测变量交叉。根据Yu[17]和Omidvar[21]等人的建议，链接检测技术分为四大类：1）扰动； 2）交互适应； 3）建立模型； 和4）随机。

1. 扰动：

• 这些方法通过扰动决策变量来检测交互，并研究由于这种扰动而导致的适应性变化。 典型的扰动方法包括以下两个步骤。 第一步是扰动决策变量并检测决策变量之间的交互。 第二步是将具有高度相互依赖性的决策变量组合到同一子组件中以进行优化。 这类方法的示例包括：通过非线性检查（LINC）进行链接识别[23]，通过对实值遗传算法（LINC-R）进行非线性检查进行链接识别[24]，自适应协进化优化[25]以及与 变量交互学习[18]。 我们提出的相互依赖变量分析可以被认为是一种扰动方法。

2. 交互适应：

• 这些方法将相互依赖检测技术融入到单个编码中，同时解决了问题。 个体之间相互依赖的变量越紧密，其重组概率就越高。 典型的例子有连锁学习遗传算法[26]和连锁进化遗传算子[27]。

3. 建模：

• 模型构建方法的经典框架包括五个步骤：a）随机初始化进化种群； b）选择一些有希望的解决方案； c）基于那些选定的有希望的解建立模型； d）从学习模型中采样新的试用解； e）重复步骤b）-e），直到满足停止标准为止。 典型代表包括分布算法（EDA）的估计[28]，紧凑型遗传算法[29]，贝叶斯优化算法（BOA）[30]和依赖结构矩阵（DSM）驱动的遗传算法[17]。

4. 随机方法：

• 与上述三种方法不同，这些方法没有使用智能过程来检测决策变量之间的交互性[7]，[21]。 他们随机排列变量以提高将相交互的变量放入相同子组件的可能性[7]。

基于学习链接的分类技术

• 注意：这是背景介绍，但不全是本文提出的工作
• 在本节中，我们介绍两种决策变量的划分方法。 第一个是将具有交互作用的决策变量划分为相同的子组件[21]。 这种划分技术对于模块化的问题是有效的。 然而，这种划分技术对于重叠和层次结构问题可能不是最好的[17]。 第二个是基于DSM聚类技术[17]划分变量。 DSM是由两个决策变量之间的相互作用构建的矩阵。 DSM聚类技术在产品设计和开发的体系结构改进中很流行。DSM聚类的目标是在同一簇内保持最大的交互，而簇间保持最小的交互。
  图2给出了DSM聚类的实例。

• 为了在聚类布置的准确性和复杂性之间做出权衡，Yu等人。 [31]提出了一种基于最小描述长度（MDL）的度量，描述为

多目标优化

连续多目标优化的规律性

• 对于大部分ZDT[34],DTLZ[35],UF[13]多目标优化测试集来说， PS分布的维度是(M-1)维，其中M是目标数量
• 举个例子，对于一个双目标的50维度的问题来说，大多数情况下，第一维控制分布，而后49维都会控制收敛，最优种群中的后49维的每一个维度的最优值都只有一个，每个个体的后49维的每个维度都会收敛到各自定义的一个特定的最优点上，而第一维则会按照分布要求分散开来。–如果实在不太理解的话可以看看benchmark给的最优点，也就是优化的目标答案。

决策变量的控制性

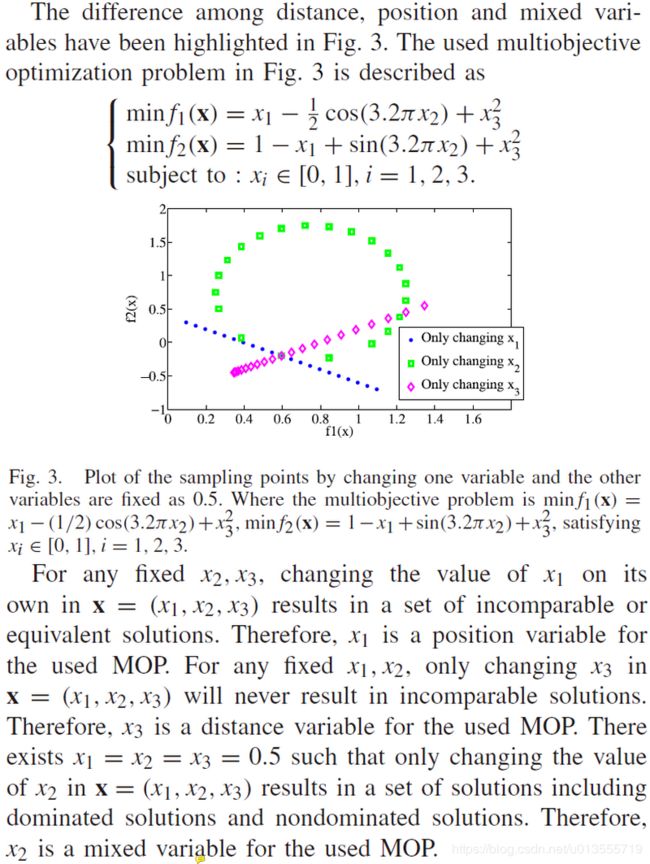
• 除了可分离性以外，决策变量根据多目标优化中与适应度景观的关系还存在着控制性。下列类型的关系很有趣，因为我们可以使用它们来将解分为多样部分和收敛部分[12]。位置变量–单纯改变position位置变量的值只会使解变为非支配关系的解或者相等的解，对应着多目标优化的多样性，而如果单纯改变一个变量的值会引起支配关系的改变或者相等的值而从不会出现废纸配的关系，即只有支配关系或者相等，即解不是变好就是变坏，而不是多样性的改变，则称这个变量为distance距离变量，如果不是位置变量或者距离变量我们将其成为mix混合变量，而混合变量在本篇论文的算法中当做多样性变量进行处理。

• 根据连续多目标优化的规律，ZDT,DTLZ,UF等多目标优化问题的位置变量和混合变量的总数是m-1,而距离变量的总数是n-m+1

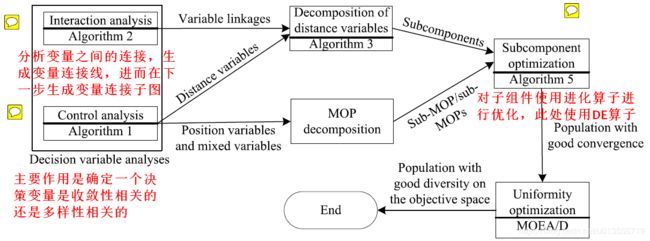
提出的算法MOEA/DVA

控制变量分析

• 位置position变量控制多样，distance变量控制收敛，具体控制变量分析方法如算法1所示：
  
• 使用UF测试用例来举例说明控制变量法来分类变量的思路
  
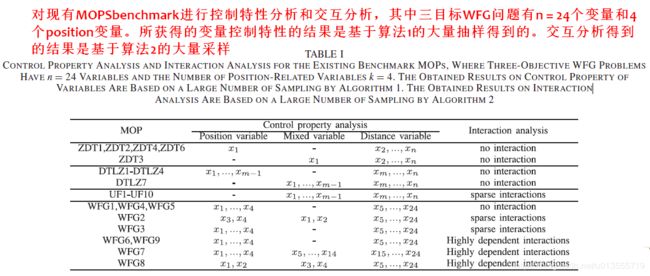
• 当所提出的算法执行决策变量的控制分析时，所需目标函数评估的次数为n×NCA，其中NCA为采样解的数量。 基于算法1的大量样本，表I总结了现有基准MOP的控制特性分析，例如连续ZDT，DTLZ，UF1-UF10和三目标WFG问题。 在此表中，三目标WFG问题的n = 24个变量，与位置position相关的变量数k = 4。
  

两个决策变量之间的相互依赖分析

• 如第II-A节所述，存在有关交互变量的不同定义。 在本文中，定义2用于分析两个决策变量之间的相互依赖关系。

两个变量相互依赖的必要条件

• 既然是必要条件，即说明是如果两个变量相互依赖，那么即会出现的性质，出现这种性质不能推导出两个变量相互依赖。但是如果这种性质或者条件不满足，则两个变量绝对不是相互依赖的。

必要条件1

• 偏导依赖
  

必要条件2

学习变量之间的交互

• 实际上，决策变量之间的相互作用可以用来将一个困难的函数分解为具有低维子组件的一组子函数[21]。 手冢等[24]使用公式（5）以不用推导就能学习演化过程中两个决策变量之间的相互作用。 对于可加分离函数，Omidvar等[21]给出了使用公式（5）识别相互作用的决策变量的理论推导。 然而，公式（5）是识别连续微分函数中两个决策变量相互作用的必要条件，但不是充分条件，如第III-B1节所述。
• 本文中使用定义二来学习两个决策变量之间的交互关系，算法2给出了实现细节，图5-7展示了ZDT1,DTLZ1,UF1 和UF8以及五个WFG问题的两个决策变量之间的交互关系
  
  
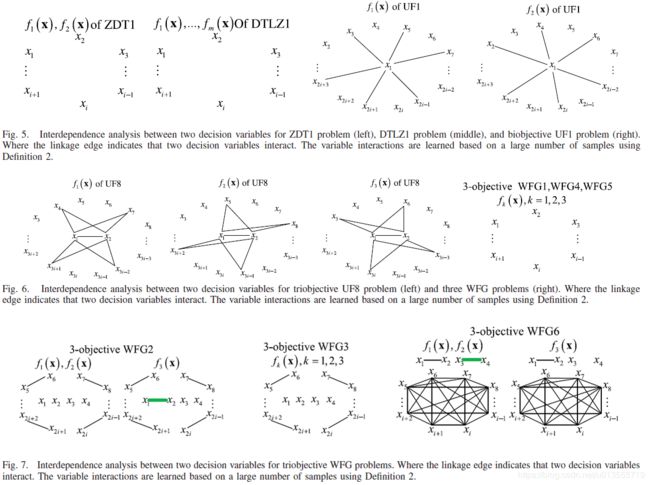
• 这些问题有两个突出的特点。 一个是在ZDT1，DTLZ1，WFG1和WFG4-WFG5问题的各个函数中不存在变量交互作用。 另一个是稀疏变量交互作用集中于UF1和UF8问题的m-1个决策变量，其中m是在（3）中定义的目标函数的数量。 通常，根据定义2，对于大多数基准测试问题（包括连续的ZDT，DTLZ，UF和WFG问题），存在稀疏变量交互。 此外，在大多数连续ZDT和DTLZ问题中都是可分离的函数。
• 当对两个变量之间的相互作用进行一种判断时，所提出的算法需要在三个点上评估目标函数的值。 因此，相互依赖性分析所需的目标函数评估数为（3/2）n（n-1）* NIA，其中m为目标函数数，n为MOP（3）中定义的决策变量数， NIA是判断两个变量之间的相互作用所需的最大尝试次数。 NIA越大，两个变量之间相互作用的判断将越精确。
• 至于为什么是三个点，下图可以解释

根据变量链接对距离变量进行分类(MOP根据变量链接的最大连接子图)

• 具体分类方式参考算法3
  
• 距离变量对收敛有影响，位置变量对多样性有影响，距离变量是MOP重点优化的难题，而位置变量是主要矛盾所在。在优化早期，我们的策略是先维持多样性的位置变量不动而只优化距离变量。
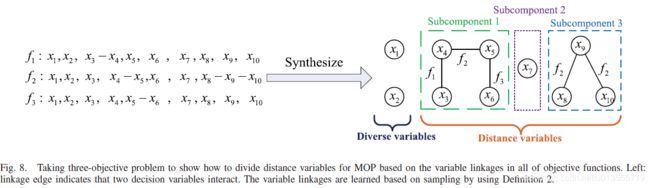
• 和单目标优化不同，MOP需要同时优化所有目标函数，因此需要在所有目标函数上对决策变量进行分类。我们将每个目标函数中的变量链接合成为一张变量链接图。 图8提出了一个三目标问题，以说明基于最大连通子图划分变量的过程。

• 注意，这些都是对收敛性的决策变量进行的工作，对于多样性的决策变量在算法早期保持不变
  
• 注意：在某些算法中会为了使subcomponents更小而打断一些链接，但是本算法暂时没有考虑这个问题，因为我们不清楚如果打断一个链接对算法最终的影响会是如何。EDA也许是一个比较好的期望能解决这个问题的算法。

提出的MOEA/DVA的框架

• 提出的MOEA/DVA的流程图如图9所示，
  

1. 决策变量分析：有两种决策变量分析 控制性分析和交互分析 控制性分析将决策变量分为收敛性变量和多样性变量，交互分析用于将收敛性变量使用变量链接进行分组。
2. 距离变量分类：收敛性变量也被称为距离变量，将高维转化为若干个低维子组件。
3. 基于多样性变量的MOP分解：一个MOP被分解为一组具有不同变量（位置变量和混合变量）值均匀分布的子MOP。
4. 子组件优化：对每个子组件独立优化以提升收敛速度。
5. 分布性优化：优化所有决策变量，包括位置变量和混合变量。 其目的是提高目标空间中种群的分布性。

• 与基于权重向量的MOEA/D [2]分解和基于偏好方向的MOEA/D-M2M [36]分解不同，本文使用各种变量（位置变量和混合变量）分解困难的MOP（3）分成一组更简单的变量分布均匀的子MOP。表II中列出了子MOP，子问题和多目标子问题之间的差异。每个子MOP是一个多目标优化问题，由原始MOP(3)定义，并具有不同变量的固定值。以带有三个决策变量的UF1问题为例来说明sub-MOP的概念。根据III-A部分的控制分析，UF1问题的x1是一个混合变量，x2和x3是距离变量。原始MOP绘制在图10(左)上，而图10(右)显示了具有恒定变量x1 = 0.25的子MOP。子MOP的主要特征是它仅具有距离变量，而没有多样性变量（位置变量和混合变量）。

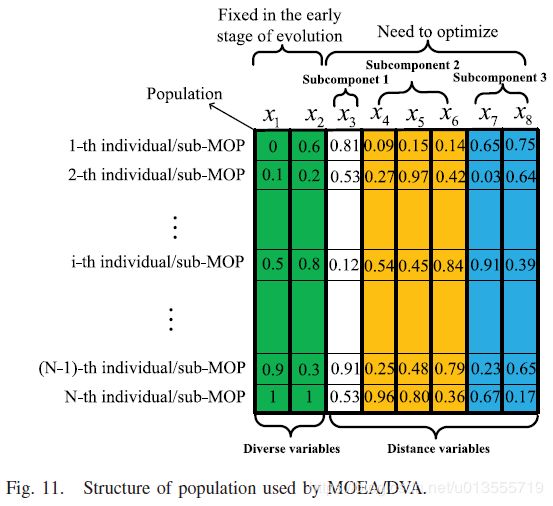
• 进化种群的结构如图11所示，其中N是种群大小。在本文中，MOEA / DVA优化了单个进化种群，所有子组件共享相同的种群。种群中的每个体都代表一个MOP。在此图中，我们假设x1和x2是多样化变量（位置变量或混合变量），而x3，x4，…。 。 。 ，x8是距离变量。距离变量分为三个独立的子分量{x3}，{x4，x5，x6}和{x7，x8}。在算法优化早期，固定位置变量，只优化距离变量。sub-MOP的特征之一是多样性变量的值在演化的早期是固定的。因此，种群中多样性变量的分布对获得的解的分布具有重要影响。为了保证进化种群的多样性，均匀采样方法[37]被用来初始化种群多样性变量的值。
  

• 表III列出了多样性变量的分解与距离变量的分解之间的差异。 基于学习到的变量链接，MOEA / DVA通过算法3将距离变量分解为一组低维子组件。算法4提供了MOEA / DVA的详细信息。 在MOEA / DVA中，这两个分解共同解决了MOP。 MOEA / DVA首先通过具有均匀分布的多样性变量将困难的MOP分解为多个更简单的子MOP。 然后，每个子MOP在发展的早期阶段都逐一优化子组件。
  
  

• 算法4的第5行对距离变量进行分组。 算法4的第9-12行类似于协作协同进化框架[7]，[21]。 算法4的第11行执行下一段介绍的子组件优化。 为简单起见，我们为MOEA / DVA中的每个子组件分配相同的计算资源。 也可以根据不同的子组件的近期性能为它们分配不同的计算资源[38]。

• 对于子组件优化，我们在MOEA/D [2]中使用进化算子。由于每个目标函数fi（x，i = 1，…，m）是连续的，因此相邻子MOP的最优解应该彼此接近。因此，有关其相邻子MOP的任何信息将有助于优化当前子MOP [2]。这些子MOP之间的邻域关系是基于其各个变量之间的欧几里得距离定义的。如果第i个子MOP的多样性变量接近第j个子MOP的多样性变量，则第i个子MOP是第j个子MOP的邻居。算法5提供了子组件优化的详细信息。在第3步中，由于在发展的早期阶段每个子MOP的多样性变量值是固定的，因此MOEA / DVA仅使用第i个MOP的后代来更新第i个MOP的当前解。为简单起见，算法5在发展的早期阶段为MOEA / DVA中的每个单独/子MOP分配了相同的计算资源。结论中将讨论更智能的MOEA / DVA版本。
  

• 最后，我们在算法4的第17行中介绍了在MOEA / DVA中进行均匀性优化的必要性。如上所述，MOEA / DVA首先将MOP分解为具有均匀分布的多样性变量的子MOP集合，并且逐个优化每个子MOP。 通过在演化的早期为多样性变量赋予统一固定值，MOEA / DVA可以在决策变量上通过均匀的多样性变量保持种群的多样性。 因此，MOEA / DVA找到的解决方案的分布高度依赖于问题从PS到PF的映射。

• 通过算法的效用评价算法的阶段–先固定多样性只对收敛性变量进行优化，然后当达到效用阈值，对所有变量进行优化

• 为了解决这一问题，利用MOEA/D对所有的决策变量进行演化，包括演化后期的多样性变量( if 效用 < 阈值 )。其目的是为了提高种群在目标空间中的均匀性。因此，MOEA/DVA的思想是逐个优化子组件，使进化种群在进化的早期阶段( if 效用 ≥ 阈值 )具有良好的收敛性。在进化后期，MOEA/DVA对包括不同变量在内的所有决策变量进行优化，使进化种群在目标空间中具有良好的均匀性。子组件优化的效用在算法6中计算。
  

参考文献

[1] K. Deb, Multi-Objective Optimization Using Evolutionary Algorithms. New York, NY, USA: Wiley, 2001.
[2] Q. Zhang and H. Li, “MOEA/D: A multi-objective evolutionary algorithm based on decomposition,” IEEE Trans. Evol. Comput., vol. 11, no. 6, pp. 712–731, Dec. 2007.
[3] N. Beume, B. Naujoks, and M. Emmerich, “SMS-EMOA: Multiobjective selection based on dominated hypervolume,” Eur. J. Oper. Res., vol. 181, no. 3, pp. 1653–1669, 2007.
[4] K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, part I: Solving problems with box constraints,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 577–601, Aug. 2014.
[5] T. Weise, R. Chiong, and K. Tang, “Evolutionary optimization: Pitfalls and booby traps,” J. Comput. Sci. Technol., vol. 27, no. 5, pp. 907–936, 2012.
[6] M. Potter and K. Jong, “A cooperative coevolutionary approach to function optimization,” in Proc. Int. Conf. Parallel Probl. Solv. Nat., vol. 2. Jerusalem, Israel, 1994, pp. 249–257.
[7] Z. Yang, K. Tang, and X. Yao, “Large scale evolutionary optimization using cooperative coevolution,” Inf. Sci., vol. 178, no. 15, pp. 2985–2999, 2008.
[8] X. Li and X. Yao, “Cooperatively coevolving particle swarms for large scale optimization,” IEEE Trans. Evol. Comput., vol. 16, no. 2, pp. 210–224, Apr. 2012.
[9] Y. Mei, X. Li, and X. Yao, “Cooperative co-evolution with route distance grouping for large-scale capacitated arc routing problems,” IEEE Trans. Evol. Comput., vol. 18, no. 3, pp. 435–449, Jun. 2014.
[10] D. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning. Reading, MA, USA: Addison-Wesley, 1989.
[11] Y. Chen, T. Yu, K. Sastry, and D. Goldberg, “A survey of linkage learning techniques in genetic and evolutionary algorithms,” Illinois Genet. Algorithms Libr., Univ. Illinois Urbana-Champaign, Urbana, IL, USA, Tech. Rep. 2007014, 2007.
[12] S. Huband, P. Hingston, L. Barone, and L. While, “A review of multiobjective test problems and a scalable test problem toolkit,” IEEE Trans. Evol. Comput., vol. 10, no. 5, pp. 477–506, Oct. 2006.
[13] Q. Zhang et al., “Multiobjective optimization test instances for the CEC 2009 special session and competition,” School Comput. Sci. Electr. Eng., Univ. Essex, Colchester, U.K., Tech. Rep. CES-887, 2008.
[14] Q. Zhang, A. Zhou, and Y. Jin, “RM-MEDA: A regularity model-based multiobjective estimation of distribution algorithm,” IEEE Trans. Evol. Comput., vol. 12, no. 1, pp. 41–63, Feb. 2008.
[15] L. Jiao, Y. Li, M. Gong, and X. Zhang, “Quantum-inspired immune clonal algorithm for global optimization,” IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 38, no. 5, pp. 1234–1253, Oct. 2008.
[16] K. Tang, X. Li, P. Suganthan, Z. Yang, and T. Weise, “Benchmark functions for the CEC’2010 special session and competition on large-scale global optimization,” Nat. Inspir. Comput. Appl. Lab., Univ. Sci. Technol. China, Hefei, China, Tech. Rep. 2010001, 2010.
[17] T. Yu, D. Goldberg, K. Sastry, C. Lima, and M. Pelikan, “Dependency structure matrix, genetic algorithms, and effective recombination,” Evol. Comput., vol. 17, no. 4, pp. 595–626, 2009.
[18] W. Chen, T. Weise, Z. Yang, and K. Tang, “Large-scale global optimization using cooperative coevolution with variable interaction learning,” in Proc. Conf. Parallel Probl. Solv. Nat., Kraków, Poland, 2010, pp. 300–309.
[19] P. Toint, “Test problems for partially separable optimization and results for the routine PSPMIN,” Dept. Math., Univ. Namur, Namur, Belgium, Tech. Rep. 83/4, 1983.
[20] B. Colson and P. Toint, “Optimizing partially separable functions without derivatives,” Optim. Methods Softw., vol. 20, nos. 4–5, pp. 493–508, 2005.
[21] M. Omidvar, X. Li, Y. Mei, and X. Yao, “Cooperative co-evolution with differential grouping for large scale optimization,” IEEE Trans. Evol. Comput., vol. 18, no. 3, pp. 378–393, Jun. 2014.
[22] D. Thierens and D. Goldberg, “Mixing in genetic algorithms,” in Proc. 5th Int. Conf. Genet. Algorithms, Urbana, IL, USA, 1993, pp. 38–45.
[23] M. Munetomo and D. Goldberg, “Identifying linkage groups by nonlinearity/ nonmonotonicity detection,” in Proc. Genet. Evol. Comput. Conf., vol. 1. Orlando, FL, USA, 1999, pp. 433–440.
[24] M. Tezuka, M. Munetomo, and K. Akama, “Linkage identification by nonlinearity check for real-coded genetic algorithms,” in Proc. Genet. Evol. Comput. Conf., Seattle, WA, USA, 2004, pp. 222–233.
[25] K. Weicker and N. Weicker, “On the improvement of coevolutionary optimizers by learning variable interdependencies,” in Proc. IEEE Congr. Evol. Comput., Washington, DC, USA, 1999, pp. 1627–1632.
[26] Y. Chen, “Extending the scalability of linkage learning genetic algorithms: Theory and practice,” Ph.D. dissertation, Dept. Comput. Sci., Univ. Illinois Urbana-Champaign, Urbana, IL, USA, 2004.
[27] J. E. Smith, “Self adaptation in evolutionary algorithms,” Ph.D. dissertation, Dept. Comput. Sci., Univ. West England, Bristol, U.K., 1998.
[28] Q. Zhang and H. Muehlenbein, “On the convergence of a class of estimation of distribution algorithms,” IEEE Trans. Evol. Comput., vol. 8, no. 2, pp. 127–136, Apr. 2004.
[29] G. R. Harik, F. G. Lobo, and D. E. Goldberg, “The compact genetic algorithm,” IEEE Trans. Evol. Comput., vol. 3, no. 4, pp. 287–297, Nov. 1999.
[30] M. Pelikan and D. Goldberg, “BOA: The Bayesian optimization algorithm,” in Proc. Genet. Evol. Comput. Conf., Orlando, FL, USA, 1999, pp. 525–532.
[31] T. Yu, A. Yassine, and D. Goldberg, “A genetic algorithm for developing modular product architectures,” in Proc. ASME Int. Design Eng. Tech. Conf., Chicago, IL, USA, 2003, pp. 515–524.
[32] K. Miettinen, Nonlinear Multiobjective Optimization. Boston, MA, USA: Kluwer Academic, 1999.
[33] C. Hillermeier, Nonlinear Multiobjective Optimization—A Generalized Homotopy Approach. Boston, MA, USA: Birkhauser, 2001.
[34] E. Zitzler, K. Deb, and L. Thiele, “Comparison of multiobjective evolutionary algorithms: Empirical results,” Evol. Comput., vol. 8, no. 2, pp. 173–195, 2000.
[35] K. Deb, L. Thiele, M. Laumanns, and E. Zitzler, “Scalable multiobjective optimization test problems,” in Proc. Congr. Evol. Comput., Honolulu, HI, USA, 2002, pp. 825–830.
[36] H. Liu, F. Gu, and Q. Zhang, “Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems,” IEEE Trans. Evol. Comput., vol. 18, no. 3, pp. 450–455, Jun. 2014.
[37] K. Fang and D. Lin, “Uniform designs and their application in industry,” in Handbook on Statistics in Industry, vol. 22. Amsterdam, The Netherlands: Elsevier, 2003, pp. 131–170.
[38] M. Omidvar, X. Li, and X. Yao, “Smart use of computational resources based on contribution for cooperative co-evolutionary algorithms,” in Proc. Genet. Evol. Comput. Conf., Dublin, Ireland, 2011, pp. 1115–1122.
[39] R. Storn and K. Price, “Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces,” J. Global Optim., vol. 11, no. 4, pp. 341–359, 1997.
[40] K. Deb, S. Agrawal, A. Pratap, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. Evol. Comput., vol. 6, no. 2, pp. 182–197, Apr. 2002.
[41] L. Tseng and C. Chen, “Multiple trajectory search for unconstrained/ constrained multi-objective optimization,” in Proc. IEEE Congr. Evol. Comput., Trondheim, Norway, 2009, pp. 1951–1958.
[42] P. Bosman and D. Thierens, “The naive MIDEA: A baseline multi-objective EA,” in Proc. Evol. Multi-Criterion Optim. (EMO), Guanajuato, Mexico, 2005, pp. 428–442.
[43] C. Ahn, “Advances in evolutionary algorithms,” in Theory, Design and Practice. Berlin, Germany: Springer, 2006.
[44] Q. Zhang, W. Liu, and H. Li, “The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances,” School Comput. Sci. Electr. Eng., Univ. Essex, Colchester, U.K., Tech. Rep. 20091, 2009.
[45] M. Liu, X. Zou, Y. Chen, and Z. Wu, “Performance assessment of DMOEA-DD with CEC 2009 MOEA competition test instances,” in Proc. IEEE Congr. Evol. Comput., Trondheim, Norway, 2009, pp. 2913–2918.
[46] E. Zitzler, L. Thiele, M. Laumanns, C. Fonseca, and V. Fonseca, “Performance assessment of multiobjective optimizers: An analysis and review,” IEEE Trans. Evol. Comput., vol. 7, no. 2, pp. 117–132, Apr. 2003.
[47] J. Derrac, S. Garca, D. Molina, and F. Herrera, “A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms,” Swarm Evol. Comput., vol. 1, no. 1, pp. 3–18, 2011.
[48] J. Durillo et al., “A study of multiobjective metaheuristics when solving parameter scalable problems,” IEEE Trans. Evol. Comput., vol. 14, no. 4, pp. 618–635, Aug. 2010.
[49] L. Marti, J. Garcia, A. Berlanga, and J. Molina, “Introducing MONEDA: Scalable multiobjective optimization with a neural estimation of distribution algorithm,” in Proc. Genet. Evol. Comput. Conf. (GECCO), Atlanta, GA, USA, 2008, pp. 689–696.
[50] L. Marti, J. Garcia, A. Berianga, and J. Molina, “Multi-objective optimization with an adaptive resonance theory-based estimation of distribution algorithm,” Ann. Math. Artif. Intell., vol. 68, no. 4, pp. 247–273, 2013.