信用风险评分的原理及实现

介绍

信用评分作用是对贷款申请人（信用卡申请人）做风险评估分值的方法。信用评分卡模型是一种成熟的预测方法，在信用风险评估和金融风控领域得到了广泛的应用。
信用评分卡可以根据客户提供的资料、客户的历史数据，对客户的信用进行评估，是建立在对大量数据进行统计分析的基础上，具有jiao较高的准确性和可靠性。
本文通过对kaggle上的Give Me Some Credit数据的挖掘分析，结合信用评分卡的建模原理，完成了数据处理、特征变量选择、变量WOE编码离散化、Logistic回归模型评估和信用评分卡评分系统的创建，对信用卡申请人是否放款提供参考。

数据清洗

• 数据探索

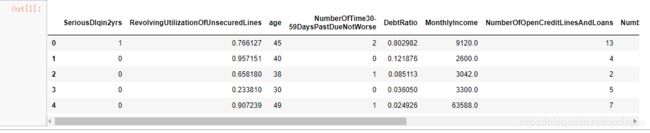
数据来源于kaggle上的Give Me Some Credit竞赛项目，其中cs-training.csv数据集大概包含15万条的样本数据，每条数据有11个变量，大致情况如下表：

• 导入数据

import numpy as np
import pandas as pd
data = pd.read_csv('D:\desktop\give me some credit\give+me+some+cridits\cs-training.csv')
data = data.iloc[:,1:]
data.head()

• 数据预览

data.shape

(150000, 11)

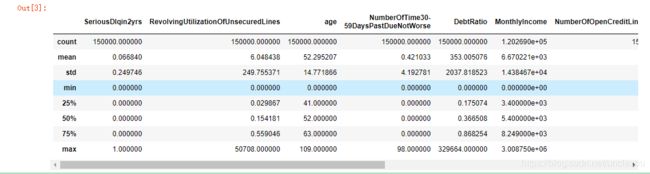
data.describe()

data.info()

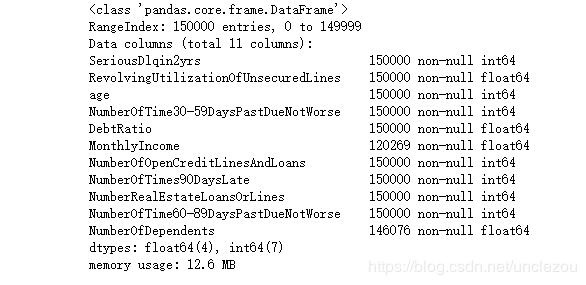
可见数据集中MonthlyIncome变量缺失数据比较多，为29731个。NumberOfDependts缺失较少，数量为3924个。

• 数据预处理

一般数据集中缺失数据非常普遍，因此在分析之前，要先处理缺失数据。
一般缺失值得处理有以下几种方法：
（1）当缺失值占比很高且变量不重要时，直接删除。
（2）根据样本之间的相似性进行填补
（3）根据变量之间的相关关系进行填补
变量MonthlyIncome缺失值较大，这里我们根据变量间的相关关系进行填补，采用随机森林拟合。

from sklearn.ensemble import RandomForestRegressor
def add_missing(df):
    process_df = df.ix[:,[5,0,1,2,3,4,6,7,8,9]]#仅选取部分列，
    #f分成已知特征值和位置特征值两部分
    know = process_df[process_df.MonthlyIncome.notnull()].as_matrix()
    unknow = process_df[process_df.MonthlyIncome.isnull()].as_matrix()
    Y = know[:,0]
    X = know[:,1:]
    rfr = RandomForestRegressor(random_state = 0, n_estimators=200, max_depth=3, n_jobs = -1)
    rfr.fit(X,Y)
    predicted = rfr.predict(unknow[:,1:])
    df.loc[df['MonthlyIncome'].isnull(), 'MonthlyIncome'] = predicted
    return df
data = add_missing(data)

NumberOfDependents变量缺失值比较少，且不是很重要，可以直接删除，对总体模型不会造成太大影响。另外对缺失值处理完之后，删除重复项。

# 缺失值和重复值删除
data=data.dropna()
data=data.drop_duplicates()

• 异常值处理

缺失值处理完毕后，要进行异常值的处理。异常值指变量中明显偏离大多数抽样数据的数值。比如恶人客户年龄小于0或者大于100，通常认为是异常值。找出样本中异常值，通常采用离群值检测的方法。这里我们采用单变量离群值检测方法来判断异常值，具体用箱线图。
绘制年龄箱线图

import matplotlib.pyplot as plt
%matplotlib inline
data_box = data.iloc[:,[2,3,7,9]]
data_box.boxplot()

从上图可以发现，age、NumberOfTime30-59DaysPastDueNotWorse、NumberOfTimes90DaysLate、NumberOfTime60-89DaysPastDueNotWorse四个变量均存在异常，因此对其做相应的剔除。
数据集中好客户为0，违约客户为1，为便于理解，正常履约客户为1，取反，只是概念上的定义，不影响实际建模。

data = data[data.age>0]
data = data[data['NumberOfTime30-59DaysPastDueNotWorse']<90]
data.iloc[:,[3,7,9]].boxplot()

• 数据切分

为验证后边模型的拟合效果，需要对数据切分，分为训练集和测试集

from sklearn.cross_validation import train_test_split
Y = data['SeriousDlqin2yrs']
X = data.ix[:,1:]
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.3, random_state = 0)
train = pd.concat([Y_train, X_train], axis = 1)
test = pd.concat([Y_test, X_test], axis = 1)
train.to_csv('D:\desktop\give me some credit\give+me+some+cridits\TrainData.csv', index = False)
test.to_csv('D:\desktop\give me some credit\give+me+some+cridits\TestData.csv', index = False)

• 单变量探索性分析

在建立模型之前，我们一般会对现有的数据进行 探索性数据分析（Exploratory Data Analysis） 。 EDA是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索。常用的探索性数据分析方法有：直方图、散点图和箱线图等
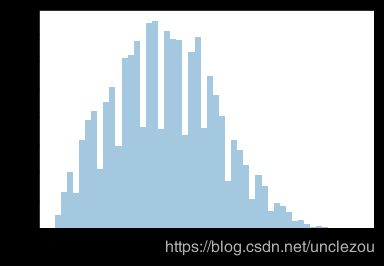
例如：我们对年龄和月收入进行分析：

import seaborn as sns
age = data.age
sns.distplot(age,kde = False)

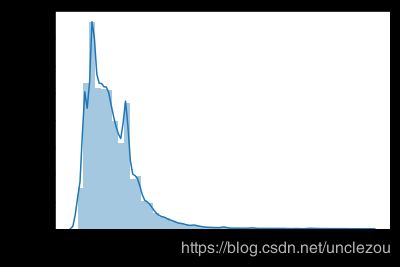
monthlyIncome = data[data.MonthlyIncome<50000].MonthlyIncome
sns.distplot(monthlyIncome)

年龄和月收入都呈正态分布，符合统计分析假设。

特征工程

变量选择属于特征工程，对于数据分析、数据挖掘来说非常重要，好的特征构建能够帮助提升模型的性能。本文我们采用信用评分卡常用的变量选择方法，通过WOE分析方法。首先对变量进行离散化处理。

• 变量分箱

本质是变量的离散化处理，信用评分卡一般常用的分箱方法有等距分箱、等深分箱、最优分箱。首选对连续变量进行最优分箱，在连续变量无法做出最优分箱时再考虑等距分箱。
最优分箱

import scipy.stats as stats
def mono_bin(Y,X,n):
    good = Y.sum()
    bad = Y.count() - good
    r = 0
    while np.abs(r)<1:
        d1 = pd.DataFrame({'X':X, 'Y':Y, 'Bucket':pd.qcut(X, n)})
        #次数n代表分箱的个数，每个分箱内数据个数相等
        d2 = d1.groupby(['Bucket'], as_index = True)
        r,p = stats.spearmanr(d2['X'].mean(), d2['Y'].mean())
        n = n-1
    #此时同时得到了某个d2和n
    print(r,n)
    d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
    d3['min'] = d2.X.min()
    d3['max'] = d2.X.max()
    d3['sum'] = d2.Y.sum()
    d3['total'] = d2.Y.count()
    d3['rate'] = d2.Y.mean()
    d3['goodattribute'] = d3['sum']/good
    #goodattribute计算方式是每个箱子里的好客户数量/数据集里总的好客户数量
    d3['badattribute']=(d3['total']-d3['sum'])/bad
    #badattribute计算方式是每个箱子里的坏客户数量/数据集里总的坏客户数量
    d3['woe']=np.log(d3['goodattribute']/d3['badattribute'])
    #之所以这样设置公式，是根据逻辑回归来定义的
    iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()
    #IV为information value表示特征的预测能力，如果分箱后，好坏样本所占的比例相差不大的话，就失去了预测能力。
    #该公式相当于求內积之和
    d4 = (d3.sort_index(by = 'min'))
    woe = list(d4.woe.values)
    print(d4,type(d4))
    print(X.name)
    print('*'*30)
    cut = []
    cut.append(float('-inf'))
    for i in range(1,n+1):
        qua = X.quantile(i/(n+1))
        cut.append(round(qua,4))
    cut.append(float('inf'))
    print(cut)
    return d4, iv, woe, cut
    #cut是对X取他的四分位，因为Y只有0  1  也不能取四分位。n=3因为最后有n-1，所以实际上是分成了四个桶，woe是四个值。goodattribute是好的属性的意思
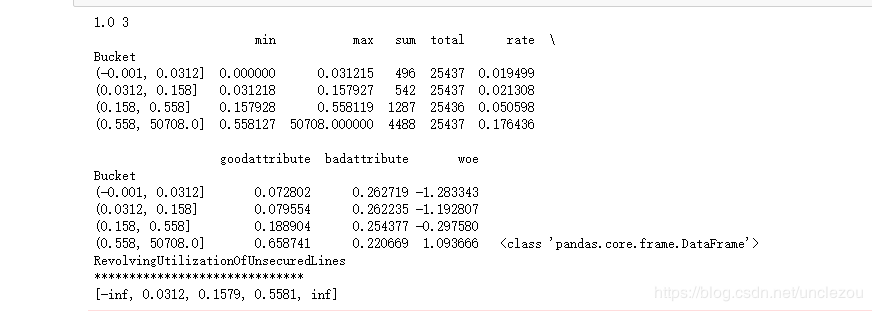
dfx1,ivx1,woex1,cutx1=mono_bin(train['SeriousDlqin2yrs'],train['RevolvingUtilizationOfUnsecuredLines'],n=10)
dfx2, ivx2,woex2,cutx2=mono_bin(train['SeriousDlqin2yrs'], train['age'], n=10)
dfx4, ivx4,woex4,cutx4 =mono_bin(train['SeriousDlqin2yrs'],train['DebtRatio'], n=20)
dfx5, ivx5,woex5,cutx5=mono_bin(train['SeriousDlqin2yrs'], train['MonthlyIncome'], n=10)

部分输出如下

针对不能最优分箱的，采用等距分箱

def self_bin(Y,X,cat):
    good=Y.sum()
    bad=Y.count()-good
    d1=pd.DataFrame({'X':X,'Y':Y,'Bucket':pd.cut(X,cat)})
    d2=d1.groupby(['Bucket'])
    d3=pd.DataFrame(d2['X'].min(),columns=['min'])
    d3['min']=d2['X'].min()
    d3['max']=d2['X'].max()
    d3['sum']=d2['Y'].sum()
    d3['total']=d2['Y'].count()
    d3['rate']=d2['Y'].mean()
    d3['goodattribute']=d3['sum']/good
    d3['badattribute']=(d3['total']-d3['sum'])/bad
    d3['woe']=np.log(d3['goodattribute']/d3['badattribute'])
    iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()
    d4=d3.sort_index(by='min')
    print(d4)
    print('-'*40)
    woe=list(d3['woe'].values)
    return d4,iv,woe

ninf=float('-inf')
pinf=float('inf')
cutx3=[ninf,0,1,3,5,pinf]
cutx6 = [ninf, 1, 2, 3, 5, pinf]
cutx7 = [ninf, 0, 1, 3, 5, pinf]
cutx8 = [ninf, 0,1,2, 3, pinf]
cutx9 = [ninf, 0, 1, 3, pinf]
cutx10 = [ninf, 0, 1, 2, 3, 5, pinf]
    
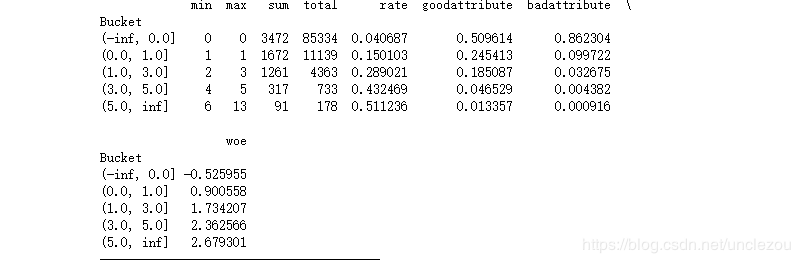
dfx3,ivx3,woex3=self_bin(train['SeriousDlqin2yrs'],train['NumberOfTime30-59DaysPastDueNotWorse'],cutx3)
dfx6, ivx6 ,woex6= self_bin(train['SeriousDlqin2yrs'], train['NumberOfOpenCreditLinesAndLoans'], cutx6)
dfx7, ivx7,woex7 = self_bin(train['SeriousDlqin2yrs'], train['NumberOfTimes90DaysLate'], cutx7)
dfx8, ivx8,woex8 = self_bin(train['SeriousDlqin2yrs'], train['NumberRealEstateLoansOrLines'], cutx8)
dfx9, ivx9,woex9 = self_bin(train['SeriousDlqin2yrs'], train['NumberOfTime60-89DaysPastDueNotWorse'], cutx9)
dfx10, ivx10,woex10 = self_bin(train['SeriousDlqin2yrs'], train['NumberOfDependents'], cutx10)

部分输出如下

• WOE

分箱之后即可求出woe值，其全称是‘weight of evidence’,即证据权重。不同变量的不同分箱分别对应着一个woe值，后边建模就是用woe值来进行拟合逻辑回归参数值。

• IV筛选

分箱之后立即求出了变量的IV值，IV全称Infomation Value，一般用来比较特征的预测能力。IV0.1以上算有预测能力，0.2以上算比较有预测能力了。
观察各变量的IV值：

import matplotlib.pyplot as plt
%matplotlib inline
ivall = pd.Series([ivx1,ivx2,ivx3,ivx4,ivx5,ivx6,ivx7,ivx8,ivx9,ivx10],index = ['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10'])
fig = plt.figure()
ax1 = fig.add_subplot(111)
ivall.plot.bar()
plt.show

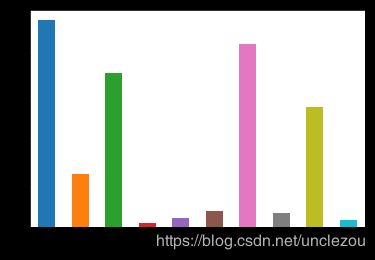
由上图可以看出，DebtRatio、MonthlyIncome、NumberOfOpenCreditLinesAndLoans、NumberRealEstateLoansOrLines和NumberOfDependents变量的IV值明显较低，预测能力差，所以删除。

• 变量相关性分析

再观察一下经过清洗后数据各变量之间的相关性。用来进一步验证IV值，作为变量筛选的依据。
相关性图我们通过Python里面的seaborn包，调用heatmap()绘图函数进行绘制，实现代码如下：

corr = data.corr()
xticks = ['x0','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
yticks = ['x0','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
fig = plt.figure(figsize = (20,10))
ax1 = fig.add_subplot(111)

sns.heatmap(corr, vmin = -1, vmax = 1, cmap = 'hsv', annot = True, square = True)
ax1.set_xticklabels(xticks, rotation = 0)
ax1.set_yticklabels(yticks, rotation = 0)
plt.show()

可见，变量之间各自的相关性不大，无需做降维处理。

模型分析

证据权重WOE转换可以将Logistic回归模型转换为标准评分卡格式，建立模型之前，需要将筛选后的变量转换为WOE值

• woe转换

前边我们已经取得了每个变量的分箱数据以及各自的WOE值，下面将数据进行替换即可。

data = pd.read_csv('D:\desktop\give me some credit\give+me+some+cridits\TrainData.csv')
#value>=cut[0]=负无穷，是肯定的
from pandas import Series
def replace_woe(series,cut,woe):
    list=[]
    i=0
    while i=0:
            if valuek>=cut[j]:
                j=-1
            else:
                j -=1
                m -= 1
                #该部分代码相当于建立两个指针，一个指针作为循环退出条件，一个保存索引号
        list.append(woe[m])
        i += 1
    return list

#顺序是第一种反着来，
data['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(data['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
data['age'] = Series(replace_woe(data['age'], cutx2, woex2))
data['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
data['DebtRatio'] = Series(replace_woe(data['DebtRatio'], cutx4, woex4))
data['MonthlyIncome'] = Series(replace_woe(data['MonthlyIncome'], cutx5, woex5))
data['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(data['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
data['NumberOfTimes90DaysLate'] = Series(replace_woe(data['NumberOfTimes90DaysLate'], cutx7, woex7))
data['NumberRealEstateLoansOrLines'] = Series(replace_woe(data['NumberRealEstateLoansOrLines'], cutx8, woex8))
data['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
data['NumberOfDependents'] = Series(replace_woe(data['NumberOfDependents'], cutx10, woex10))

test= pd.read_csv('D:\desktop\give me some credit\give+me+some+cridits\TestData.csv')
    # 替换成woe
test['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(test['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
test['age'] = Series(replace_woe(test['age'], cutx2, woex2))
test['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(test['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
test['DebtRatio'] = Series(replace_woe(test['DebtRatio'], cutx4, woex4))
test['MonthlyIncome'] = Series(replace_woe(test['MonthlyIncome'], cutx5, woex5))
test['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(test['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
test['NumberOfTimes90DaysLate'] = Series(replace_woe(test['NumberOfTimes90DaysLate'], cutx7, woex7))
test['NumberRealEstateLoansOrLines'] = Series(replace_woe(test['NumberRealEstateLoansOrLines'], cutx8, woex8))
test['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(test['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
test['NumberOfDependents'] = Series(replace_woe(test['NumberOfDependents'], cutx10, woex10))

• Logistics回归模型建立

import statsmodels.api as sm
Y=data['SeriousDlqin2yrs']
X=data.drop(['SeriousDlqin2yrs','DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)

X1=sm.add_constant(X)
logit=sm.Logit(Y,X1)
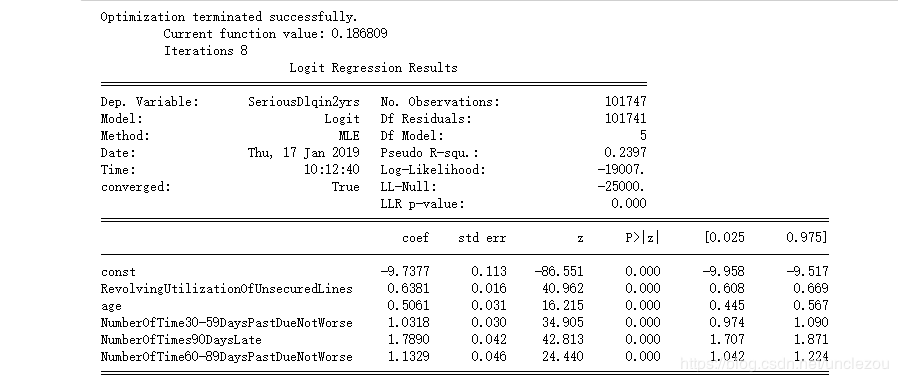
result=logit.fit()
print(result.summary())

逻辑回归各变量对应的参数都已求出

• 模型验证

from sklearn.metrics import roc_curve,auc
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['FangSong']    # 指定默认字体
matplotlib.rcParams['axes.unicode_minus'] = False
Y_test=test['SeriousDlqin2yrs']
X_test=test.drop(['SeriousDlqin2yrs','DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)

#通过ROC曲线和AUC来评估模型的拟合能力。
X2=sm.add_constant(X_test)
resu=result.predict(X2)
fpr,tpr,threshold=roc_curve(Y_test,resu)
# %f,%d,%s输出    
rocauc=auc(fpr,tpr)
plt.plot(fpr,tpr,'b',label='AUC=%0.2f'% rocauc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()

从上图可知，AUC值为0.85，说明模型的预测能力较好，正确率较高。证明了用当前这五个特征，去构成信用评分卡的一部分分值是有效的，预测能力是较好的。

信用评分卡的构建

Logistic回归在信用评分卡开发中起到核心作用。由于其特点，以及对自变量进行了证据权重转换（WOE），Logistic回归的结果可以直接转换为一个汇总表，即所谓的标准评分卡格式。

由逻辑回归的基本原理，我们将客户违约的概率表示为p，则正常的概率为1-p。因此，可以得到：

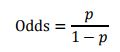
评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义，即可表示为下式：

Score = A -B*log(Odds)

其中，A和B是常数。 式中的负号可以使得违约概率越低，得分越高。通常情况下，这是分值的理想变动方向，即高分值代表低风险，低分值代表高风险。

式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下，需要设定两个假设：
（1）给某个特定的比率设定特定的预期分值；
（2）确定比率翻番的分数（PDO）
根据以上的分析，我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值应该为P+PDO。

假设 设定评分卡刻度使得比率为{1:20}（违约正常比）时的分值为600分，PDO为20分
A为offset，B为factor
代入式中，可以得到如下两个等式：

620 = offset - factor * log(20*2,base = 10)
600 = offset - factor * log(20)

求得：
factor = - 20 / math.log(2) #p值（比例因子）
offset = 600 - 20 * math.log(20) / math.log(2) #

个人总评分=基础分+各部分得分
基础分为:
baseScore = a*factor+offset (a为拟合出的回归系数中的截距w0)

# 计算分数函数
def get_score(coe,woe,p):
    scores=[]
    for w in woe:
        score=round(coe*w*p,0)
        scores.append(score)
    return scores

# 部分评分x1,x2,x3,x7,x9
# j和m相当于j是移动光标，m是跟着j，确定数的
def compute_score(series,cut,scores):
    i=0
    list=[]
    while i=0:
            if value>=cut[j]:
                j=-1
            else:
                j=j-1
                m=m-1
        list.append(scores[m])
        i=i+1  
    return list
# list就是再x1里面挑一个值，这个值和series【i】是对应的
#score是等于模型系数*woe(一个woe对应一个score)*p值（比例因子） 

coe=[9.738849,0.638002,0.505995,1.032246,1.790041,1.131956]      # 回归系数
import math
p = - 20 / math.log(2)     #p值（比例因子） ，前有负号
q = 600 - 20 * math.log(20) / math.log(2)    # 
basescore = round(q - p * coe[0], 0)
print(basescore)
# 因为第一个是常数项
#构建评分卡时候只需要选出那些，IV值高的特征就行，最后相加得到总分
x1 = get_score(coe[1], woex1, p)
x2 = get_score(coe[2], woex2, p)
x3 = get_score(coe[3], woex3, p)
x7 = get_score(coe[4], woex7, p)
x9 = get_score(coe[5], woex9, p)
# x1的四个值分别对应cut的四个区间.PDO Point Double Odds,    就是好坏比翻一倍， odds就是好坏比
print(x1)
print(x2)
print(x3)
print(x7)
print(x9)
test1=pd.read_csv('D:\desktop\give me some credit\give+me+some+cridits\TestData.csv')
# 先构建好Series再加上也可以
# round可能要用到import math.
# 只需要对test计算分值，因为我们前面构建模型用的是train，计算分值要用test
test1['BaseScore']=Series(np.zeros(len(test1))+basescore)
test1['x1']=Series(compute_score(test1['RevolvingUtilizationOfUnsecuredLines'],cutx1,x1))
test1['x2'] = Series(compute_score(test1['age'], cutx2, x2))
test1['x3'] = Series(compute_score(test1['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, x3))
test1['x7'] = Series(compute_score(test1['NumberOfTimes90DaysLate'], cutx7, x7))
test1['x9'] = Series(compute_score(test1['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, x9))
test1['score']= test1['BaseScore']+test1['x1']+test1['x2']+test1['x3']+test1['x7']+test1['x9']
test1.to_csv('D:\desktop\give me some credit\give+me+some+cridits\scoredata.csv')

基础分值：795.0
5个变量每个分段对应的分值：
[24.0, 22.0, 5.0, -20.0]
[-8.0, -6.0, -4.0, -3.0, -1.0, 3.0, 7.0, 14.0, 16.0]
[16.0, -27.0, -52.0, -70.0, -80.0]
[20.0, -102.0, -142.0, -166.0, -160.0]
[9.0, -60.0, -88.0, -95.0]

test1.loc[:,['SeriousDlqin2yrs','BaseScore', 'x1', 'x2', 'x3', 'x7', 'x9', 'score']].head(15)

总结

本文通过对Kaggle上的数据Give Me Some Credit的挖掘分析，结合评分信用卡的建立原理，通过数据预处理、变量选择、变量分箱、建模分析等方法，使用随机森林拟合了缺失值，使用Pandas包进行了数据清理，并使用matplotlib和seaborn绘图包进行了数据可视化，且使用logistic回归模型，最后利用模型验证过部分变量，创建了一个简单的信用评分系统。

Give me some cridets数据集
链接：https://pan.baidu.com/s/1ePsCQ5Sj1AtUX1WVJi1n5w
提取码：q5u2