SVM——详细讲解SMO算法优化两个变量以及变量的选择

一、SMO(序列最小最优化)优化两个变量

以非线性支持向量机的对偶问题为例，使用SMO算法求解该对偶问题的最优参数α^* 。
非线性支持向量机的对偶问题如下：

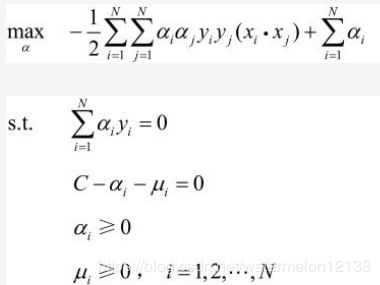
对偶问题转换：(如何转换请看这篇博客)

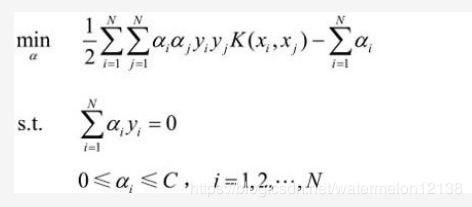
存在最优解(w^*,b^* ,ξ^*, α^* ,μ^*)使得w^*,b^* ,ξ^* 是原始问题的最优解且 α^* 是对偶问题的最优解的充要条件是(w^*,b^* ,ξ^*, α^* ,μ^*)满足KKT条件。
KKT条件如下：

上述的KKT条件太过分散，很难看出关联，所以先对KKT条件进行化简：
首先令g(x_i) =w·x_i+b ,
当α_i = 0时，由C - α_i - μ_i = 0可得u_i=C(C不等于0)，由A和C知y_i(w·x_i+b)-1+ ξ_i >=0。因为u_i不等于0，由B知ξ_i=0，所以y_i(w·x_i+b)-1>=0即y_i(w·x_i+b) >= 1即 y_ig(x_i) >= 1。
当0 < α_i < C 时, 由C - αi - μi = 0可得 u_i = C - α_i ，因为0 < α_i < C，所以μ_i > 0。因为0 < α_i < C ，由A和C知y_i(w·x_i+b)-1+ ξ_i =0。因为u_i不等于0，由B知ξ_i=0，所以y_i(w·x_i+b)-1 =0即y_i(w·x_i+b) = 1即 y_ig(x_i) = 1。
当 α_i = C时，由A可得y_i(w·x_i+b)-1+ ξ_i =0，即y_i(w·x_i+b) + ξ_i = 1 (D式) ，又因为C - α_i - μ_i = 0，所以μ_i =0，所以由B可得ξ_i>=0。所以由D式可得 y_ig(x_i) <= 1。
化简后的KKT条件如下：

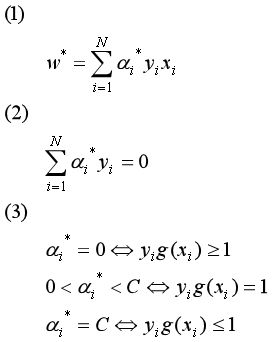
直接求出最优的参数α(α₁,α₂, …, α_N)是很难的，SMO算法的思想是每次只优化α的两个分量，最终使得α的所有分量都满足KKT条件。

SMO算法从这里开始

1.1 SMO优化选中的两个变量
现在开始讲如何优化参数α中被选中的两个分量，首先列出对偶问题及其KKT条件。
对偶问题：

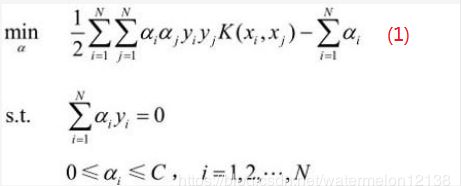
KKT条件：

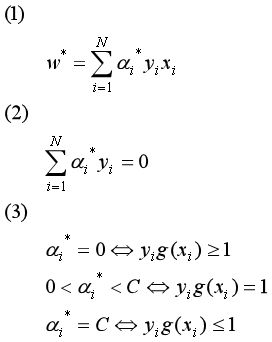
初始化α(α₁,α₂, …, α_N) = (0,0,…,0)，假设SMO算法选中的两个分量是α₁和α₂，如何来选这两个分量后一节会讲，将α₁,α₂原来的值称为α₁^old和α₂^old，那么现在要来求新的值α₁^new和α₂^new ,相当于更新优化了α₁和α₂。其它分量(α₃,α₄, …, α_N)相当于是固定的(已知的)，那么(1)式转换成只含变量α₁和α₂的(2)式如下：

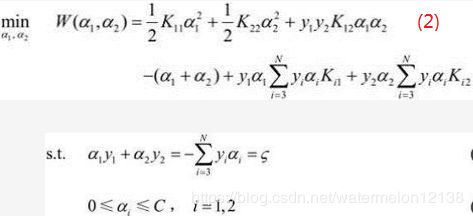
其中K_ij = K(x_i, x_j)，表示核函数，ζ为常数。

###################################
（#号之内的内容是个小插曲，可以暂时跳过，后面回过头再来看）

先来确定一下α₁或α₂的取值范围，这确定α₂的取值范围，因为0<=α₁<=C，0<=α₂<=C，α₁y₁ + α₂y₂ = ζ，所以α₁和α₂肯定位于[0, C]的矩形框内且位于直线α₁y₁ + α₂y₂ = ζ上。
当y₁和y₂异号时，α₁y₁ + α₂y₂ = ζ 等价于 α₁ - α₂ = |ζ|，假设ζ >0 可得下图：

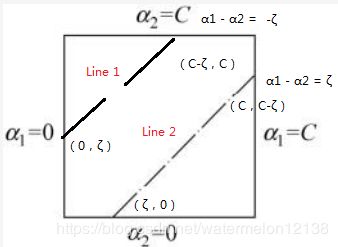
Line1的两个端点坐标分别是(0, ζ)和(C-ζ，C)，α₁ - α₂ = -ζ，所以两个端点坐标等价于(0, α₂ - α₁ )和(C - α₂ + α₁，C )。
Line2的两个端点坐标分别是(ζ，0)和(C，C-ζ)，α₁ - α₂ = ζ，所以两个端点坐标等价于(α₁ - α₂，0)和(C ，C + α₂ - α₁ )。
坐标转换后得如下图：

α2的取值范围要么是Line1上的[ α₂ - α₁，C]，要么是Line2上的[0，C + α₂ - α₁]，现在想将α2的取值范围变成 L<=α₂<=H这种形式，那么怎么来做呢？
令L = max( 0，α₂ - α₁)，H= min(C，C + α₂ - α₁)，当L=0时，说明α₂ - α₁ < 0，所以 C + α₂ - α₁ < C，所以H = C + α₂ - α₁，则L<=α₂<=H表示 α₂位于Line2上，它的取值范围是 0<=α₂<=C + α₂ - α₁；当L=α₂ - α₁时，说明α₂ - α₁ > 0，所以 C + α₂ - α₁ > C，所以H = C，则L<=α₂<=H表示 α₂位于Line1上，它的取值范围是 α₂ - α₁<=α₂<=C。
所以当y₁和y₂异号时，L = max( 0，α₂ - α₁)，H= min(C，C + α₂ - α₁)，用 L<=α₂<=H 就能表示α₂的取值范围。

同理当y₁和y₂同号时，α₂位于下图中的某条直线上，这里不再赘述，直接上结论。L= max(0, α₂ + α₁ - C)，H = (C，α₂ + α₁)，用 L<=α₂<=H 就能表示α₂的取值范围。

###################################

记g(x_i) =w·x_i+b,由KKT条件(1)可得：

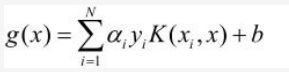
记E_i = g(x_i) - y_i，表示预测值与真实值之差，如下：

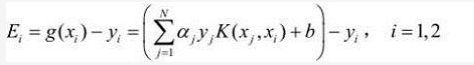
记v_i 如下：

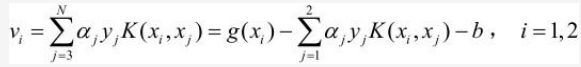
通过v_i只含 α₁ ， α₂两个变量的式(2)变成式(3)如下：

因为α₁y₁ + α₂y₂ = ζ，y_i² = 1，所以α₁ = （ζ - α₂y₂）y₁，将该式带入式(3)中就得到了只含α₂一个变量的式(4)，如下：

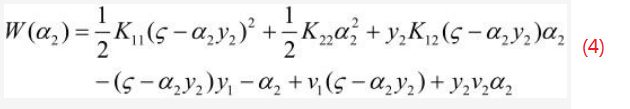
然后式(4)对α₂求导并令其等于0就可以解出α₂^new,unc ：


之所以称它为α₂^new,unc ，是因为α₂^new,unc不一定符合α₂的取值范围，如何来求α₂的取值范围请看上文用#号括起来的内容，将α₂^new,unc转换成最终的α₂^new，具体操作过程如下：

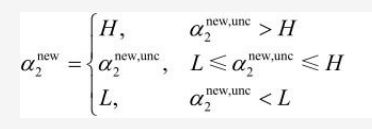
上式就确保了α₂更新后的值α₂^new 符合α₂的取值范围。
因为α₁和α₂满足以下约束：

更新优化α₁和α₂后得到α₁^new和α₂^new ，因为(α₃,α₄,…,α_N)没有变动，所以α₁^new和α₂^new 依然满足上述约束：

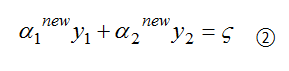
上面两个约束相减，可得：

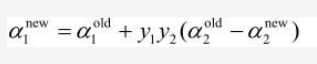
到此为止被选中的α₁和α₂优化结束。

1.2 SMO计算阈值b^new和差值E_i
因为α₁和α₂已经优化结束，当然要更新α₁和α₂对应的E₁和E₂，求b^new就是为了求E₁和E₂。
当0<α₁^new 1g(x₁)=1，也就是g(x₁)=y₁，即

于是：

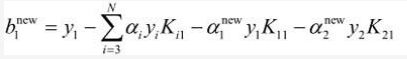
E₁ = g(x₁) - y₁，即：

b₁^new等式的前两项可以写为：

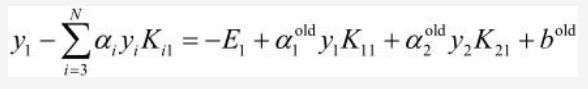
所以b₁^new最终等于：

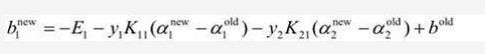
同理如果0<α₂^new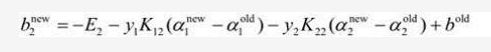
更新b的规则如下：
如果0<α₁^new new = b₁^new；如果0<α₂^new new = b₂^new；如果都不满足则b^new = (b₁^new + b₂^new)/2
其实更新b不是最终目的，我们的最终目的是更新E_i：

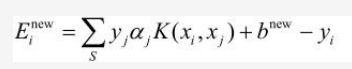
其中S是所有支持向量x_j的集合。

二、SMO算法变量的选择

2.1 第一个变量的选择
SMO算法称选择第一个变量为外层循环，这个变量需要选择在训练集中违反KKT条件最严重的样本点。对于每个样本点，要满足的KKT条件我们在上面已经讲到了：

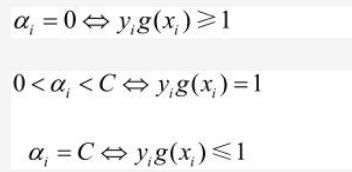
一般来说，我们首先选择违反0<α_iig(x_i)=1这个条件的最严重的点，比如0<α_ii, y_i)，y_ig(x_i)远远大于1或远远小于1，所以点(x_i, y_i)就是违反0<α_iig(x_i)=1这个条件的最严重的点。如果0<α_ii=0⇒y_ig(x_i)≥1 和 α_i=C⇒y_ig(x_i)≤1的点。

2.2 第二个变量的选择
SMO算法称选择第二个变量为内层循环，假设我们在外层循环已经找到了α₁, 第二个变量α₂的选择标准是让|E₁−E₂|有足够大的变化。由于α₁定了的时候,E₁也确定了，所以要想|E₁−E₂|最大，只需要在E₁为正时，选择最小的E_i作为E₂， 在E₁为负时，选择最大的E_i作为E₂，可以将所有的E_i保存下来加快迭代。

如果内存循环找到的点不能让目标函数有足够的下降， 可以采用遍历支持向量点来作为α₂,直到目标函数有足够的下降， 如果所有的支持向量作α₂都不能让目标函数有足够的下降，可以跳出循环，重新选择α₁。（支持向量点是位于分界间隔上的点或位于间隔之内的点或分错的点)

三、SMO算法总结

输入是m个样本(x₁,y₁),(x₂,y₂),…,(x_m,y_m)，其中x为n维特征向量，y为二元输出，值为1或者-1，精度为e。
输出是近似解α
1)取初始值α⁰ = 0，k=0
2)按照2.1节的方法选择α₁^k ，按照2.2节的方法选择α₂^k ，求出新的α₂^new,unc。

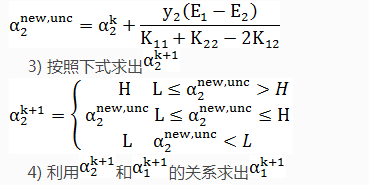
5)按照1.2节的方法计算b^k+1 和E_i。