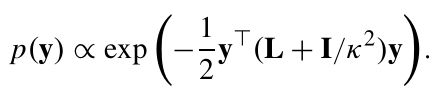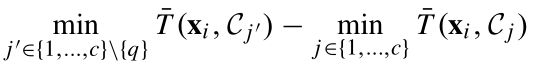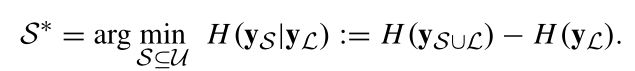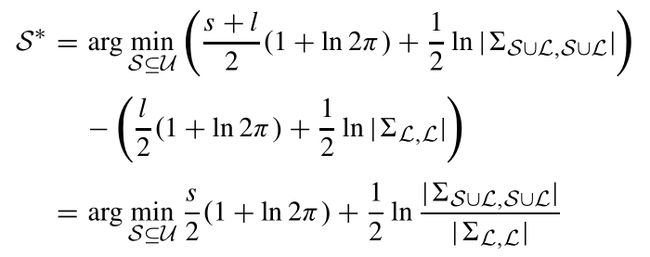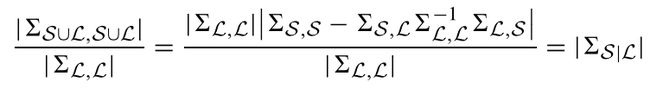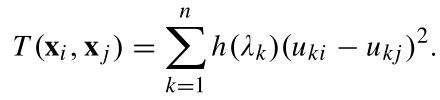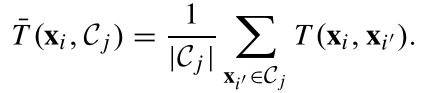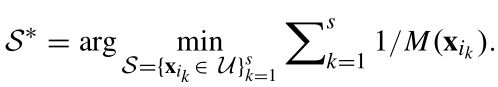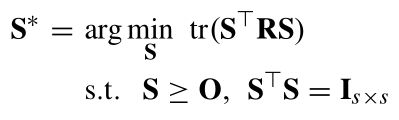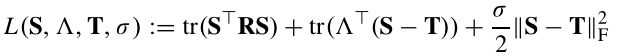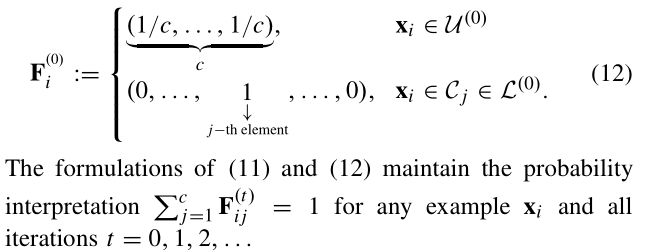《Label Propagation via Teaching-to-Learn and Learning-to-Teach》阅读笔记
原论文链接:http://ieeexplore.ieee.org/document/7447818/
下载链接: http://www.escience.cn/system/download/79676
传统的机器学习技术分为两类,一类是无监督学习,一类是监督学习。
无监督学习只利用未标记的样本集,而监督学习则只利用标记的样本集进行学习。但在很多实际问题中,
只有少量的带有标记的数据,因为对数据进行标记的代价有时很高,比如在生物学中,对某种蛋白质的
结构分析或者功能鉴定,可能会花上生物学家很多年的工作,而大量的未标记的数据却很容易得到。这
就促使能同时利用标记样本和未标记样本的半监督学习技术迅速发展起来。
1.论文简介
标签传播的局限性:
- 现有的基于图论的传播算法通常同样地对未标记的例子进行处理,并将种子标签传送到与标记的例子相连的未标记的例子。然而,这种流行的传播方案很可能会产生不准确的传播,因为它不足以处理含糊但关键的数据点(例如异常值)。
- 某些情况下可能会变得脆弱。例如,跨越不同类别的桥点以及异常类别与正常类别的异常距离很可能误导传播并导致错误分类。原因是这个标签由传统方法产生的传播完全由给定例子(包括标记和未标记的例子)之间的邻接关系来控制,其中种子标记盲目地扩散到未标记的邻居而没有考虑繁殖的难度或风险。因此,如果上面提到的歧义点被错误地激活以接收传播的标签,则可能发生不同类别之间的相互标签传输。
为此,本文通过评估可靠性和可区分性,处理不同等级的无标签样本,并通过操纵传播序列从
简单到难点的例子明确优化传播质量。特别地,我们提出了一种新颖的迭代标签传播算法,其
中每个传播在两个范例之间交替,即教学和学习教学(TLLT)。在教学步骤中,学习者在由教
师指定的最简单的未标记的例子上进行传播。在学习到教学的步骤中,教师结合学习者的反馈
来调整后续最简单的例子的选择。所提出的TLLT策略严格地提高了标签传播的准确性,使得我
们的算法对于调整参数的值(例如图形构造中使用的高斯内核宽度)具有很强的鲁棒性。
2.本文工作
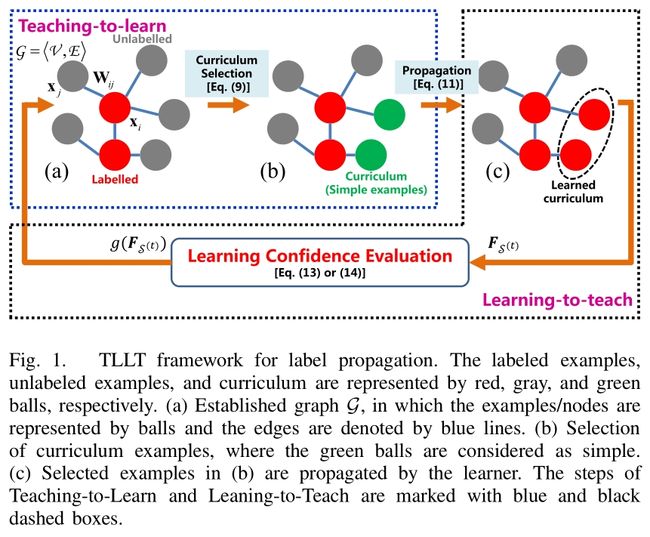
如图所示TLLT框架。图中红色代表已标注对象,灰色代表未标注对象,绿色代表课程。
(a)建立一个图G,其中样本/节点用球来表示,边缘用蓝线表示。
(b)选择课程对象,这里绿色的球被认为是最简单的。
(c)在前面被选择的对象通过学习者传播。
教师的角色是为了选择最简单的例子[即课程;参见图1(b)(绿色球)]从未标记的例子(灰色球)的池中作为当前传播。这个选择是通过求解一个优化问题来实现的,该优化问题整合了每个未标记的例子的可靠性和可辨性。 在学习教学步骤中,学习者激活最简单的例子来使用[5]中提出的经典方法进行标签传播[见图1(c)],同时将其学习信心传递给教师 协助教师决定后续最简单的例子。这样的两步过程迭代,直到所有的未标记的例子得到妥善处理。由于老师和学习者之间的交互作用,最初难以处理的(即不明确的)例子在较晚的时候被处理,从而可以通过利用以前学到的知识来可靠地标记它们。
3. TEACHING-TO-LEARN STEP
1)问题定义
假设有一组样例X:
其中前l个对象为已标注样本L,剩余的u个对象为未标注样本U。并且n=l+u,l< 为了记录标注样本x1~xn的标签用标签矩阵F定义: 这里的第i行向量: 且满足: Fij表示xi属于第j类Cj的概率。 假设每个样本xi都与随机向量yi是关联的,yi为xi的分类标签。 我们可以把这种在图上的传播看做一种高斯处理,将其模型作为随机变量有y上的多元高斯分布。即: I为适当尺寸的单位矩阵,在本篇文章中k固定为100, 然后,我们定义了可靠性与可分辨性来评估选择样本的难易程度。 定义1:如果条件熵H(yS|yL)很小,则对于标注集S属于U是可靠的。 定义2:如果对于任意的xi,使得 的值越大,课程S属于U是可分辨的。 定理1中,找出对于对于标记样本最可靠的课程S: 基于适当的高斯处理,可推导: 又由于: 得到最可靠的课程S为: 定理2中: 表示为从Xi到Xj,又从Xj回到Xi的时间。 表示为Xi到所有j类样本中的平均时间。 M(xi)——表示对于的明确性: M(xi)越大,表明xi明显倾向明确的分类。 所以,最具有可辨别性的课程S为: 综合考虑可靠性和可辨别性,课程S的选择为: 这里α>0为调节参数。 考虑到种子标签将首先传递到未标记的例子,它们在L中的直接与标记例子相邻,我们收集这些标记在一组基数为b例子B。因为只有s(s < b)需要的例子B不同,我们引入一个二元选择矩阵S, 正交约束加入一个S,确保S中没有重复的样本。 形式可改写成: 我们注意到问题(8)属于整型规划,通常是比较困难的。为了易于处理,我们把离散约束变为连续非负约束。这样我们可以更简单地解决这个问题: R为一个正定矩阵。 S的优化问题就是一个非凹优化问题,可以采用局部增广拉格朗日乘法器解(PALM)解决。但若对增广拉格朗日表达式中加入非负约束,而正交性约束被明确地保留并强加在用于更新S的子问题上。这样对于S的子问题是Stiefel-manifold约束优化问题,可以通过曲线搜索方法有效解决。 这里的局部增广拉格朗日: 注意:算法2生成的解S是连续的,不符合问题(8)中的原始二进制约束。 因此,我们通过简单的贪婪程序将S离散为二进制值。 详细地说,我们找到S中最大的元素,并记录它的行和列; 然后从未记录的列和行中搜索最大的元素并重新标记; 此过程重复,直到找到s元素。 这些S元素的行表明所选定的最简单的示例将被传播。 这一部分首先介绍了一个学习者,它是传播的模型,然后阐述如何为后续的教学建立学习反馈。 这里首先我们假设: 传播的模型如(11)所示。 而xi标签向量的初始状态为: 在传播了t次后,学习者应向教师提供学习的反馈,并协助教师确定(t+1)的课程。然而,第t次迭代生成的的传播标签的正确性并不确定,这里引入了一个学习置信度,探索用来盲评估第t次学习的表现。 具体而言,我们将学习置信度限制在[0,1]的范围内,其中如果S(t)中的所有课程实例获得确定的标签向量,则获得1;如果课程实例分配了类似的标签,则获得0 值覆盖所有可能的类。 举例说:假设我们总共有c=3个分类类别,那么对于单个样本xi,如果它有一个标签向量Fi = [1,0,0],[0,1,0]或[0,0,1],它是一个很好地学习,这意味着xi绝对属于1,2或3类。 相反,如果xi的标签向量是Fi = [1/3, 1/3,1/3],它将是一个不好的学习例子,因为[1/3,1/3,1/3]不能提供任何提示确定它的分类。 所以针对样本S我们整合了学习置信度,提出了学习验证函数。 根据定理3,提出了两种学习验证函数,分别利用了Fs(t)的范数和熵: 基于定义的学习验证函数,第(t+1)次课程的中样本的数量是如下式(15)所示: TLLT处理直到所有未标记样本都被学习,同时获得一个标签矩阵F。然后,设置如下初始状态: 再使用下面的迭代公式驱动整个传播过程达到一个稳定状态。 这里的θ>0 是平衡从其他示例传播的标签和由TLLT过程产生的F的权重参数。 我们设置θ= 0.05来执行最终结果,以最大限度地保留教学和学习生成的标签。 通过使用Perron Frobenius理论,我们取F(t)的极限如下: A.课程选择
B.优化
4. LEARNING-TO-TEACHSTEP
5.总结