图像平滑
Smoothing, also called blurring, is a simple and frequently used image processing operation.
本质就是把某点的像素值转换为其及其周围像素值的不同权重的叠加.h(k,l)即为卷积核,或者叫滤波器filter.
有几种常见的filter
- Normalized Box Filter
- Gaussian Filter
- Median Filter
- Bilateral Filter
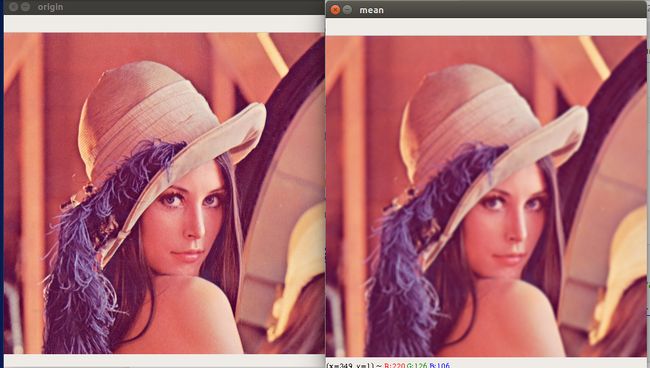
均值滤波
img2= cv2.blur(img,(5,5))The call blur(src, dst, ksize, anchor, borderType) is equivalent to boxFilter(src, dst, src.type(), anchor, true, borderType).
https://docs.opencv.org/master/d4/d86/group__imgproc__filter.html#ga8c45db9afe636703801b0b2e440fce37
高斯滤波
即假设某一位置的像素和其邻域像素符合高斯分布.具体的说的话,就是每一位置的像素的权重符合高斯分布.这样的话,给定一个高斯分布,及高斯核的大小,则可以计算出周边n个像素的权重值.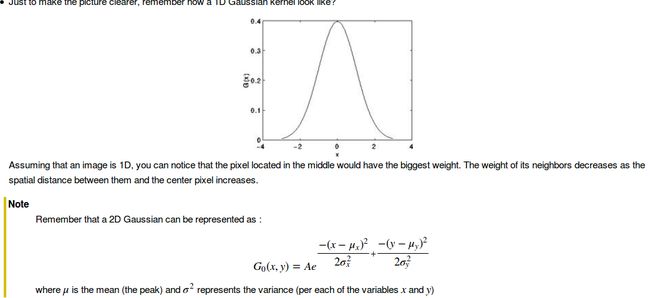
上图展示了一维度的高斯分布图和二维高斯分布的公式. 图像是2维度的.(即行维度和列维度确定一个像素点的位置).
高斯滤波的具体计算过程.可以参考https://blog.csdn.net/zr459927180/article/details/52400641
opencv中获取高斯核心的函数为getGaussianKernel,但是这个获取的一维的高斯核.对图像来说,以3*3邻域而言,我们应该得到一个3*3的权重矩阵.可以如下得到:
kernal_x = cv2.getGaussianKernel(3,-1)
kernal_y = cv2.getGaussianKernel(3,-1)
kernal_filter = np.dot(kernal_x,kernal_y.T)
print(kernal_filter)输出如下:
[[0.0625 0.125 0.0625]
[0.125 0.25 0.125 ]
[0.0625 0.125 0.0625]]则中间元素的亮度值经高斯转换后为0.0625 x p(0,0) + 0.125 x p(0,1) + .... + 0.0625 x p(2,2),可以看到权重矩阵相加等于1.
这里,我们举例用了3 x 3的高斯核,实际上并不限定高斯核一定要是正方形.
回到cv的GaussianBlur(),
其参数sigmaX,sigmaY即x,y方向上的高斯分布的标准差.这样就可以求得不同方向上的高斯矩阵,再做矩阵乘法,即得到m x n的权重矩阵.进而求得高斯转换后的图像.
我们知道高斯分布(也叫正态分布)的特点为,标准差越大,分布越分散,标准差越小,分布越集中.所以调大GaussianBlur()中的sigmaX,sigmaY将使得图像中的每个像素更多地参考周边像素,即更为平滑或者说模糊.
参见下图:(这张图选的不好,高斯模糊效果不明显,但还是可以看出图3更模糊一些)
import cv2
import numpy as np
def test():
imgname = "/home/sc/opencv-3.4.3/samples/data/lena.jpg"
img = cv2.imread(imgname)
img2 = img.copy()
#img2 = cv2.blur(img,(5,5))
img2 = cv2.GaussianBlur(img,(5,7),1)
img3 = cv2.GaussianBlur(img,(5,7),100)
kernal_x = cv2.getGaussianKernel(3,0)
kernal_y = cv2.getGaussianKernel(3,0)
kernal_filter = np.dot(kernal_x,kernal_y.T)
print(kernal_filter)
kernal_x = cv2.getGaussianKernel(3,5)
kernal_y = cv2.getGaussianKernel(3,5)
kernal_filter = np.dot(kernal_x,kernal_y.T)
print(kernal_filter)
#return
cv2.imshow("origin",img)
cv2.imshow("dst",img2)
cv2.imshow("dst3",img3)
k=cv2.waitKey()
if k == 27:
cv2.destroyAllWindows()
test()![]()
从getGaussianKernel()的输出可以明显地看出来,标准差调大时,权重矩阵的变换.
中值滤波
即把像素值变为邻域像素值的中位数.
注意,kernal的大小必须为奇数.
import cv2
def test():
imgname = "/home/sc/opencv-3.4.3/samples/data/lena.jpg"
img = cv2.imread(imgname)
dst = cv2.medianBlur(img, 1)
dst2 = cv2.medianBlur(img, 11)
cv2.imshow("origin",img)
cv2.imshow("dst",dst)
cv2.imshow("dst2",dst2)
k=cv2.waitKey()
if k == 27:
cv2.destroyAllWindows()
test()双边滤波
双边滤波函数是 cv2.bilateralFilter() ,双边滤波能在保持边界清晰的情况下有效的去除噪音。但是这种操作与其他滤波器相比会比较慢.我们已经知道高斯滤波器是求中心点邻近区域像素的高斯加权平均值。这种高斯滤波器只考虑像素之间的空间关系,而不会考虑像素值之间的关系(像素的相似度)。所以这种方法不会考虑一个像素是否位于边界。因此边界也会被模糊掉,而这不是我们想要的。
双边滤波在同时使用空间高斯权重和灰度值相似性高斯权重。空间高斯函数确保只有邻近区域的像素对中心点有影响,灰度值相似性高斯函数确保只有与中心像素灰度值相近的才会被用来做模糊运算。所以这种方法会确保边界不会被模糊掉,因为边界处的灰度值变化比较大.
简单滴说就是,在生成周边像素的权重矩阵时,如果发现旁边的像素值和当前的像素值差异很大,就只给差异很大的那个元素分配很小的权重,这样"大的突变差异就被保留了".
双边滤波的原理可以参考:https://blog.csdn.net/shenziheng1/article/details/50838970
dst = cv2.bilateralFilter(img, 9, 75, 75)效果图:
可以看到纹理被模糊掉了,但是边界还是很好地保留了.
参考:参考:
https://blog.csdn.net/shenziheng1/article/details/50838970
https://blog.csdn.net/GiffordY/article/details/91891920