第一章、微型计算机基础
第一讲:微型计算机的基本组成及各个部分的功能与作用(理解)
数字计算机,它是一种能够存储程序,能自动连续地对各种数字化信息进行算术逻辑运算的快速工具。在这一定义中包含两个重要的基本概念:信息数字化,存储程序工作方式。它们是了解计算机组成及工作机制的基本出发点。
计算机分类:数字型,模拟型,数模混合
一、基本概念
1、存储程序工作方式与冯诺依曼机
1945年,冯诺依曼在领导设计EDBAC计算机的过程中,提出了现代数字计算机的若干设计思想,后被人们称之为冯诺依曼体系
冯诺依曼体制系的核心概念----存储程序工作方式。仍是目前采用的原则。其要点是:
(1)采用二进制代码表示数据和指令
计算机是处理信息的工具,所处理的信息称为数据
计算机的具体的工作表现为执行程序,而程序的最终可执行形态是指令序列,即若干用数字代码表示的机器指令
数据和指令都采用二进制代码表示,则它们在外形上并无区别都是由0和1组成的代码序列,只是各自约定的含义不同而已
(2)采用存储程序工作方式
A、事先编制程序
B、将程序存储于计算机的存储器中
C、计算机在运行时自动地连续地从存储器中依次取出指令加以执行
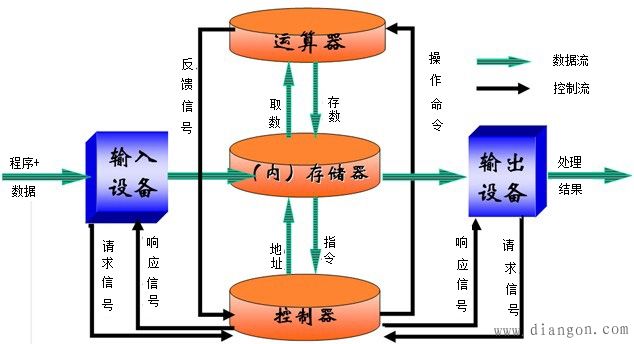
(3)硬件系统由五大部分组成
计算机硬件系统由运算器、存储器、控制器、输入设备、输出设备五大部件构成(填空或选择)
2、计算机系统的软硬件组成与层次结构
(1)硬件系统
计算机的硬件是指系统中可触摸到的物理设备实体
(2)软件系统
计算机软件通常是泛指各类程序和文件。由于它们在计算机中的表示是一些不能直接触摸到的二进制信息,所以被称为软件
(3)软件分类
系统软件:操作系统、语言处理程序等
应用软件:通用软件、用户程序等
二、计算机发展简史
(1)硬件
第一台计算机是1946年问世的,距今不到55年,尽管这台被命名为ENIAC(Electronic Numerical Intgerator And Calculator)的计算机现在看起来是那样“笨拙”和“低级”,可在当时却轰动了世界,它的意义在于宣告人类开始了一个新时代--------信息革命时代
50多年来,电子计算机的发展是那样的目不暇接、那样的绚丽多彩,所以计算机发展的划分就显得的困和多样化。早先,学术界常常以器件内部作为划分的标准
第一代:电子管计算机。时间1946-1957年
第二代:晶体管计算机。时间1958-1964年
第三代:中小规模集成电路(IC)计算机,时间1965-1970年
第四代:大规模集成电路(LSI)和超大规模(VLSI)计算机,时间1970-
(2)软件
计算机硬件发展的同时,软件始终伴随其步伐迅猛发展。就以计算机的语言而言,也划分了若干时代:
第一代:机器语言。每条指令用二进制编码
第二代:汇编语言。用符号编程,和具体机器指令和硬件有关
第三代:高级语言
第四代:它实际上是在高级语言的基础上集成的模块化语言,它有更强编程功能
三、计算机分类及微型计算机的特点
按计算机规模分,传统上分巨型机,大型机,中型机,小型机,微型机,单片机等。这种划分综合了计算机的运算速度,字长,存储容量,输出输入能力,价格等指标。
但由于计算机性能的日新月异地变化,划分的标准也就逐渐失去了意义
微型计算机的特点,与大、中、小型计算机的区别,就在于其中中央处理器(CPU)是集中在一块硅片上的,而大、中、小型计算机的CPU则是由相当多的电路(集成电路)组成的
第二讲:微型机的基本工作过程(理解)
第三讲:计算机中的编码、数制及其转换(掌握)
(1)二进制
二进制数的表示
二进制数仅有两个计数符号;0,1
二进制数的算术运算
加法规则:“逢2进1”
减法规则:“借1出2”
乘法规则:“逢0出0,全1出1”
十六进制数的加、减运算
加法运算:“逢16进1”
减法运算:“借1当16”
4、为什么要用十六进制
简化书写,便于记忆
5、数制的转换
(1)任意进制与十进制之间的相互转换方法
任意进制转换成十进制
方法是:按权展开后相加即可(举例)
二进制:10.1B 权值:1 0 -1 基数:2
1*2^1+0*2^0+1*2^-1=2.5
(2)十进制整数转换为任意进制整数
方法是:首先用基数除十进制数可得商及余数,此余数为任意进制代码的最低位。再用基数除该商数,又可得商数和余数,则此余数为次低位的任意进制代码。用同样的方法继续用基数除下去,直到商为零为止。(举例)
十进制:3
3/2 1
1/2 1
0
3的二进制是11B
(3)十进制小数转换为任意进制小数
方法是:不断用基数去乘要转换的十进制小数,将每次所得到的整数依次记为X1,X2,若乘积的小数部分最后能为0,那么最后一次乘积的整数部分记为Xm,则书写为0,X1,X2------Xm
0.25*2 0
0.50*2 1
注意;一个十进制小数不一定能完全准确地转换成一个二进制小数。可根据精度要求取有限位表示。
十进制整数到任意进制整数的转换
1、 十进制整数转换成其它进制整数
除R取余 R为基数
书写方式: 从下往上从左往右
2、 十进制小数转换成其它进制小数
乘R取整 R为基数
书写方式; 从上往下从左往右
例:将13.75转换为二进制数
分别将整数部分和小数部分进行转换;整数部分:13=1101B
小数部分:0.75=0.11B 因此,13.75=1101.11B
(4)二进制数与十六进制数之间的转换
因为2^4=16,即可用四位二进制数表示一位十六进制数,所以可得到如下所述的二进制数与十六进制数之间的转换方法
将二进制数转换为十六进制数的方法:以小数点为界,向左(整数部分)每四位一组,高位不足4位时补0;向右(小数部分)每四位为一组低位不足4位时补0.然后分别用一个16进制数表示每一组中的4位二进制数。
将十六进制数转换为二进制数的方法:直接将每一位十六进制数写成其对应的四位二进制数
例:1101110.01011B=0110,1110,1000B=6E.58.H
2F.1BH=10 1111.0001 1011B
(5)二进制数与八进制数之间的相互转换
方法是:一位八进制数相当于三位二进制数
第四讲:无符号二进制数的算术运算和逻辑运算
(一) 无符号数的概念
逻辑代数初步
在计算机中存在着大量这样得逻辑电路,逻辑关系非常复杂。逻辑代数是研究复杂的逻辑关系的有力工具,人们也往往称之为布尔代数或开关代数
逻辑代数和一般代数不同,一般代数变量的值是连续的,而逻辑代数中变量的值只有两个:1和0.尽管在逻辑代数中某些运算规则和普通代数相同,但逻辑代数中的0和1的意义绝不是代数中的数值0和1,它只代表某种物理量的状态,因此,逻辑代数运算含义和普通代数完全不同。
布尔代数也和普通代数一样,可以写成下面表达式:Y=f(A、B、C。。。。。)
但它有两个特点:
A、B、C、D只有两种可能,即0或1
注意;布尔代数的变量只代表事物的两个不同的状态或性质。如“开”或“关”
函数f只有三种基本运算,即“与”,“或”,“非”
注意:逻辑运算都是独立的按位进行,而和其它位的运算结果无关
1、“或”运算
逻辑表达式为:
Y=A+B
上式或运算的意义是;逻辑变量A或B中,只要有一个1,则逻辑变量Y的值为1
或运算的基本规则是:
0+0=0 A+0=A
0+1=1 A+1=1
1+0=1 A+A=A
1+1=1
2、“与”运算
逻辑表达式为:
Y=A*B
上式与运算的意义是:逻辑变量A或B中,只有都为1,则逻辑变量Y的值为1.否则为0
与运算的基本规则是:
0·0=0 A·0=0
0·1=1 A·1=A
1·0=0 A·A=A
1·1=1
3、“非”(反)运算
逻辑表达式为:
Y=A-
非运算的基本规则是;
0-=1 A+A-=1
1-=0 A·A-=0
A--=A
和普通代数一样,逻辑代数也有类似的运算法则,如逻辑代数同样适用于交换律,结合律和分配律三种运算法则
4、摩根定理
除了以上定律外,逻辑代数中还有自己的一些特殊定律。例如:摩根定律。在电路设计中,人们手边有时没有“与”门,而只有“或”和“非”门。或者只有“与”门和“非”门,没有“或”门,利用摩根定律可以帮助你解决元件互换问题
A+B=A·B
A·B=A+B
四、逻辑电路
最基本的逻辑电路有三种:与门电路,或门电路和非门电路
非门 1 o
或门 >=1
与门 &
真值表:当人们遇到一个问题时,常常把各种因素全部考虑进去,然后研究结果,真值表也就是这种考虑问题的方法的一种表格形式。
与门电路真值表
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 0 |
0 |
0 |
| 1 |
1 |
1 |
或门电路真值表
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
非门电路真值表
| A |
Y |
| 0 |
1 |
| 1 |
0 |
第五讲:运算中的溢出
溢出概念及检测方法
在计算机中,若采用定点小数,数的表示范围为|X|<1,如果出现运算结果超出数的表示范围的现象,就称为溢出。
两个正数相加,结果为负(即:大于机器所能表示的最大正数),称为上溢
两个负数相加,结果为正(即:小于机器所能表示的最小负数),称为下溢
运算出现溢出,结果就是错误的
例:x=+0.1011,y=+0.1001,求x+y。
解:
[x]补=0.1011,[y]补=0.1001
[x]补 0.1011
+ [y]补 0.1001
[x+y]补 1.0100
两数相加,结果为负,显然是错误。
--运算中出现了“上溢”
检测方法;
1、 双符号位法(变形补码法)
用两个相同的符号位表示一个数的符号,左边第一位为第一符号位,是结果的真正符号位,相邻的位第二符号位。定义双符号位的含义为:00表示正号,11表示负号,01表示产生正向溢出,10表示负向溢出。
已知;x=0.1011,y=0.0111,求x+y=?
解:
[x]补=00.1011,[y]补=00.0111
[x]补=00.1011
+[y]补=00.0111
[x+y]补=01.0010
2、 单符号位操作检测方法
当操作数中的加数与被加数符号相同时,若运算结果的符号与操作数的符号不一致,表示溢出;否则,表示没有溢出。而当加数和被加数符号不同时,相加预算的结果是绝对不会溢出的
第六讲:机器数的表示及运算
一、数据与字符的机内表示
数值数据的表示
真值与机器数
真值:正、负符号加二进制绝对值
例:-0010011B、+1011001B
机器数:在机器中使用的连同数符一起数码化的数
例:10010011B、01011001B
数学计算中,数有不同的类型(如整数,小数,实数,复数),数也有不同的取值范围,有不同的数值精度要求。那么,在计算机中要表示一个机器数,也应考虑一些的因素,现在我们提炼出三个主要因素:
1.机器数的范围
字长为8位,无符号整数的最大值是(111111111)B=(255)D
此时机器数的范围是0-255
字长为16位,无符号整数的最大值是(111111111111111)B=(FFFF)H=(65535)D 此时机器数的范围是0-65535
2.机器数的符号
在算术运算中,数据是有正有负的,将这类数据称为带符号数
为了在计算机中正确地表示带符号数,通常规定每个字长的最高位为符号位,并用0表示正数,用1表示负数
3.机器数中小数点的位置
在机器中,小数点的位置通常有两种约定:
一种规定小数点的位置固定不变,这时的机器数被称为定点数
另一种规定小数的位置可以浮动,这时的机器数被称为浮点数
(1)定点小数
定点小数是纯小数,是将小数点固定在符号位d0之后,数值最高位d1之前,这就是定点小数形式。其格式如下所示
| d0 |
d1 |
d2 |
…… |
dn |
·隐含小数点的位置
(2)定点整数
定点整数是纯整数,是将小数点固定在数的最低位之后,这就是定点整数形式。其格式如下:
| d0 |
d1 |
d2 |
…… |
dn |
·隐含小数点位置
例:
X=+1010110à纯整数:X=01010110
正数,符号位取0
Y=-1101001à纯整数;Y=11101001(原码)
负数,符号位取1
X=+0.11011à纯小数;X=0.11011
符号位取0
Y=-0.10101à纯小数:Y=1.10101
符号位取1
非常大和非常小数
如何用定点数来表示非常大(e.g.太阳的质量2*10^+33克)的数和非常小(e.g.电子的质量9*10^-28克)的数?
用科学计数法计数时,我们会引入比例因子10^34和10^-27,使其数值部分绝对值小于1,即:
2*10^+33=0.2*10^34
9*10^-28=0.9*10^-27
浮点表示法
浮点表示法与数学中的科学计数法相似,是指计算机中的小数点位置不是固定的,或者说是“浮动”的。对于任何一个二进制数N都可表示为:
N=2^+-E*(+-M)
式中,M称为N的尾数,是一个纯小数,E是数N的阶码,是一个整数
例:1110001B=2^+7*0.1110001
0.001110001B=2^-2*0.1110001
计算机中机器浮点数由以下部分组成:
| Es |
E1……En |
Ms |
D1……Dn |
| 阶符 |
阶码值 |
数符 |
尾数值 |
1110001B=2^+7*0.1110001
现忽略机器字长,且设阶码为3位
则有机器浮点数:011101110001
浮点数的规格化
例:156.78 =15.678*10^1
=1.5678*10^2
=0.15678*10^3=R^E*M
多种数据形式,那么,计算机中究竟采用哪种数据形式?
对于二进制数
1011.1101 =0.10111101*2^+4
=10.111101*2^+2
二进制数=1.0111101*2^3(规格化表示法)=1.0111101*2^+11(规格化表示法)
=R^E*M
二、数的机器码表示------有符号数的表示方法
数有正、负之分,在计算机中,采用数的符号和数值一起编码的方法来表示数据
常用的表示方法:原码表示法,反码表示法,补码表示法和移码表示法
(1)原码
正数的符号位为0,负数的符号位为1,其它位按照一般的方法来表示数的绝对值。用这样的表示方法得到的就是数的原码
例:当机器字长为8位二进制数时;
X=+1011011 [X]原码=01011011
Y=-1011011 [y]原码=11011011
注意:0使用原码有两种表达形式
[+0]原=00000000
[-0]原=10000000
[+0]反=00000000
[-0]反=11111111
[+0]补=00000000
[-0]补=100000000 1以溢出等于00000000
(2)反码
对于一个带符号数来说,正数的反码与其原码相同,负数的反码与其原码除符号以外的各位按位取反
例:当机器字长位8位二进制数时:
X=+1011011 [X]原码=01011011
[X]反码=01011011
Y=-1011011 [Y]原码=11011011
[Y]反码=10100100
(3)补码
正数的补码与其原码是相同的,负数的补码为其反码最低位加1
例:(1)X=+1011011 (2)Y=-1011011
X原=01011011 Y原=11011011
X反=01011011 Y反=10100100
X补=01011011 Y补=10100101
(4)移码
移码也叫增码,它常以整形式用在计算机浮点数的阶码(表示指数)中。若纯整数X为n位(包括符号位),则共移码定义为:
[X]移=2^n-1+[X]补 2^n-1<=X<=2^n-1-1
求移码的方法:
根据定义
将该数补码的符号位求反即得该数的移码
即:移码与补码的形式相同,只是符号位相反
(5)BCD码
BCD(Binary Coded Decimal)码又称为“二一十进制编码”,专门解决用二进制数表示十进制数的问题。最常用的是8421编码,其方法是用4位二进制数表示1位十进制数,自左至右每一位对应的位权是8、4、2、1,如果按位权求和,和数或等于该数码所对应的十进制数。
例:二进制数10001001B
采用BCD码表示为十进制数89D
(6)非数值数据在机内的表示
字符的编码
在计算机中除了数值之外,还有一类非常重要的数据,那就是字符,如英文的大小写字母(A,B,C……,a,b,c…),数字字符(0,1,2……9)以及其它常用符号(如:?、=、%、+等)。在计算机中,这些符号都是用二进制编码的形式表示,即每一个字符被赋予一个惟一固定的二进制编码,为了统一,人们制定了编码标准。目前,一般都是采用美国标准信息交换码,他使用七位二进制编码来表示一个符号,通常把它称为ASCLL码,由于用七位码来表示一个符号,故该编码方案中共有128个符号(2^7=128),编码从(0000000)2到(1111111)2
(7)汉字的编码
计算机要处理汉字信息,就必须首先解决汉字的表示问题,同英文字符一样,汉字的表示也只能采用二进制编码形式,目前使用比较普遍的是我国指定的汉字编码标准GB2312-80,该标准共博包含一、二级汉字6763个,其他符号682个,每个符号都是用14位(两个7位)二进制数进行编码,通常叫做国际标码。如“啊”的国标码为1110000,1100001.新的国标汉字库已包括两万多个汉字和字符
三、定点加法、减法运算
(1)补码加法运算
补码运算的优点;可将减法运算转化为加法运算,从而简化机器内部硬件电路的结构
补码运算的特点;符号位和数值位一起参加运算,只要结果不发生溢出,得到的就是本次运算结果
补码的加法运算规则:
公式:[x]补+[y]补=[x+y]补
即:任意两个数的补码之和等于该两个数之和的补码
例:x=0.1001,y=0.0101,求x+y
[x]补=0.1001,[y]补=0.0101
[x]补 0.1001
+ [y]补 0.0101
[x+y]补 0.1110
所以 x+y=+0.1110
(2)补码的减法运算
公式:[x]补-[y]补=[x-y]补=[x+(-y)]补=[x]+[-y]补
即;两数相减可化为被减数的补码与减数补码取补的加法运算
例:已知机器字长8位,x=44D,y=53D,求x-y=?
解:x=00101100,y=00110101
[x]补=00101100 [-y]补=11001011
[x]补=00101100
+ [-y]补=11001011
[x-y]补=11110111
补码=反码+1
[x-y]反码=11110110
[x-y]原-0001001
(x-y)2=-0001001,x-y=-9
第七讲:基本的逻辑门及常用逻辑部件
逻辑电路
最基本的逻辑电路有三种:与门电路、或门电路和非门电路
非门(反相器) Y=A-
或门 Y=A+B
与门 Y=AB
真值表:。。。。。
在三个基本门 电路的基础上还可以发展成其他电路。其中缓冲器的作用是改变输出电阻,以提高带负载能力
异或门(异门)
异或非(同门)
缓冲器(变阻器)
真值表:。。。。。。
1、 半加器电路:由以上逻辑关系式可得到一个一位半加器
2、 全加器;由以上逻辑关系式可得到一个一位全加器
3、 半加器及全加器
进A0 B0 进A1 B1
出C1 HA 出CI+1 FA 进C1
出S0 出S1
半加器不需要考虑进位 全加器需要考虑进位