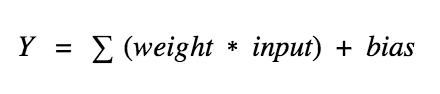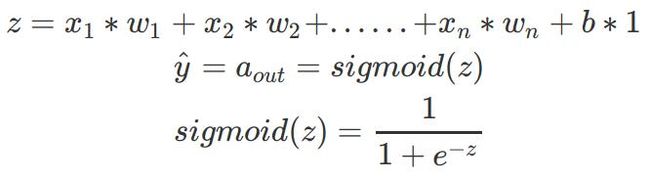理解什么是人工智能,以及机器学习和深度学习如何影响它,是一种不同凡响的体验。在 Mate Labs 我们有一群自学有成的工程师,希望本文能够分享一些学习的经验和捷径,帮助机器学习入门者理解一些核心术语的意义。并且,出于此目的我们创建了一个平台,任何人可通过它构建机器学习&深度学习模型,甚至无需写一行代码。
神经元(节点)—神经网络的基本单元,它包括特定数量的输入和一个偏置值。当一个信号(值)输入,它乘以一个权重值。如果一个神经元有 4 个输入,则有 4 个可在训练中调节的权重值。
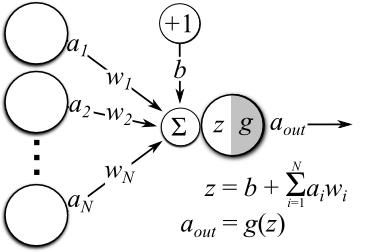
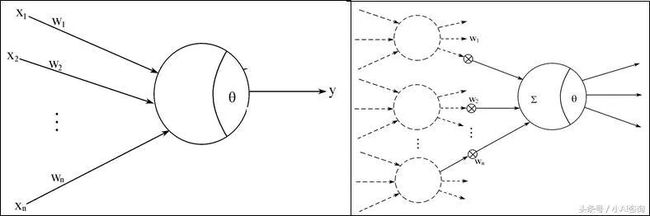
神经网络中一个神经元的运算
连接—它负责连接同层或两层之间的神经元,一个连接总是带有一个权重值。训练的目标是更新这一权重值以降低损失(误差)。
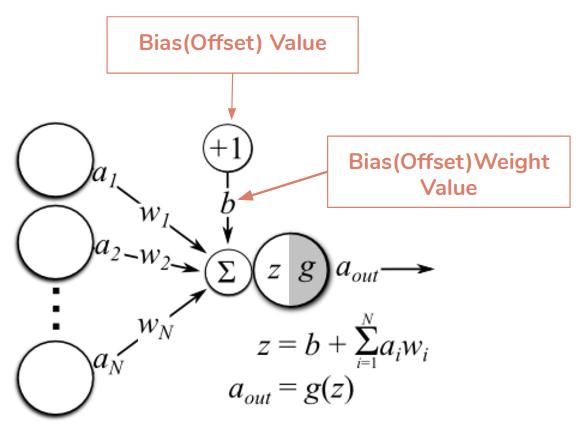
偏置(Offset)—它是神经元的额外输入,值总是 1,并有自己的连接权重。这确保即使当所有输入为 0 时,神经元中也存在一个激活函数。
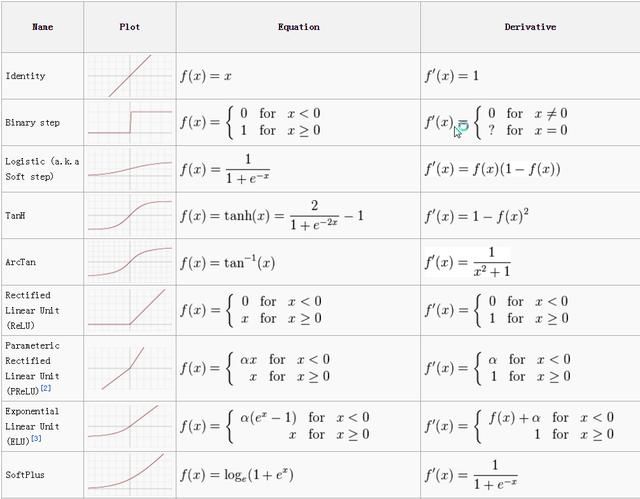
激活函数(迁移函数)—激活函数负责为神经网络引入非线性特征。它把值压缩到一个更小范围,即一个 Sigmoid 激活函数的值区间为 [0,1]。深度学习中有很多激活函数,ReLU、SeLU 、TanH 较 Sigmoid 更为常用。
各种激活函数
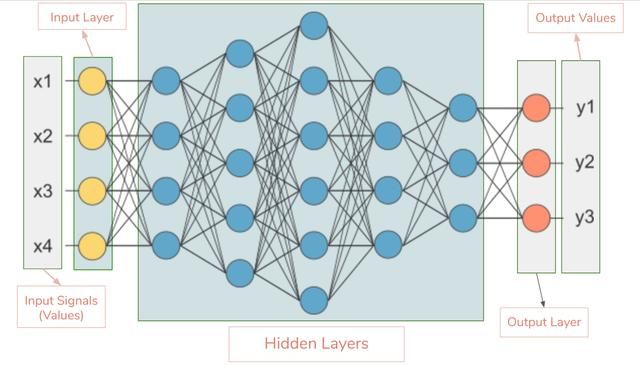
基本的神经网络设计
输入层—神经网络的第一层。它接收输入信号(值)并将其传递至下一层,但不对输入信号(值)执行任何运算。它没有自己的权重值和偏置值。我们的网络中有 4 个输入信号 x1、x2、x3、x4。
隐藏层—隐藏层的神经元(节点)通过不同方式转换输入数据。一个隐藏层是一个垂直堆栈的神经元集。下面的图像有 5 个隐藏层,第 1 个隐藏层有 4 个神经元(节点),第 2 个 5 个神经元,第 3 个 6 个神经元,第 4 个 4 个神经元,第 5 个 3 个神经元。最后一个隐藏层把值传递给输出层。隐藏层中所有的神经元彼此连接,下一层的每个神经元也是同样情况,从而我们得到一个全连接的隐藏层。
输出层—它是神经网络的最后一层,接收来自最后一个隐藏层的输入。通过它我们可以得到合理范围内的理想数值。该神经网络的输出层有 3 个神经元,分别输出 y1、y2、y3。
输入形状—它是我们传递到输入层的输入矩阵的形状。我们的神经网络的输入层有 4 个神经元,它预计 1 个样本中的 4 个值。该网络的理想输入形状是 (1, 4, 1),如果我们一次馈送它一个样本。如果我们馈送 100 个样本,输入形状将是 (100, 4, 1)。不同的库预计有不同格式的形状。
权重(参数)—权重表征不同单元之间连接的强度。如果从节点 1 到节点 2 的权重有较大量级,即意味着神将元 1 对神经元 2 有较大的影响力。一个权重降低了输入值的重要性。权重近于 0 意味着改变这一输入将不会改变输出。负权重意味着增加这一输入将会降低输出。权重决定着输入对输出的影响力。
前向传播
前向传播—它是把输入值馈送至神经网络的过程,并获得一个我们称之为预测值的输出。有时我们也把前向传播称为推断。当我们馈送输入值到神经网络的第一层时,它不执行任何运算。第二层接收第一层的值,接着执行乘法、加法和激活运算,然后传递至下一层。后续的层重复相同过程,最后我们从最后一层获得输出值。
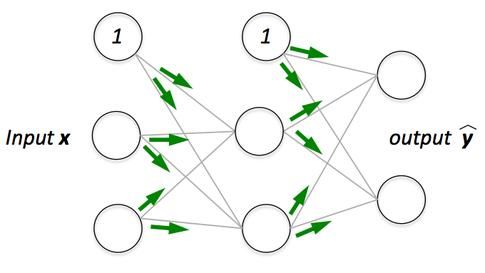
反向传播
反向传播—前向传播之后我们得到一个输出值,即预测值。为了计算误差我们对比了带有真实输出值的预测值。我们使用一个损失函数(下文提及)计算误差值。接着我们计算每个误差值的导数和神经网络的每个权重。反向传播运用微分学中的链式法则,在其中我们首先计算最后一层中每个误差值的导数。我们调用这些导数、梯度,并使用这些梯度值计算倒数第二层的梯度,并重复这一过程直到获得梯度以及每个权重。接着我们从权重值中减去这一梯度值以降低误差。通过这种方式我们不断接近局部最小值(即最小损失)。
学习率—训练神经网络的时候通常会使用梯度下降优化权重。在每一次迭代中使用反向传播计算损失函数对每一个权重的导数,并从当前权重减去导数和学习率的乘积。学习率决定了更新权重(参数)值的快慢。学习率应该尽可能高而不会花费太多时间达到收敛,也应该尽可能低从而能找到局部最优。
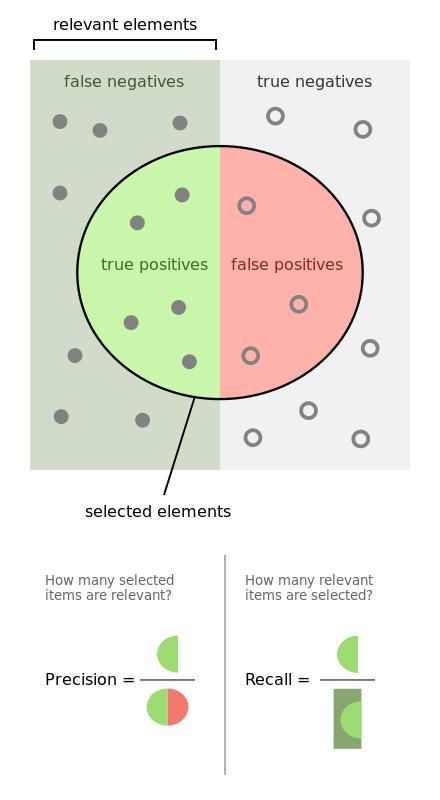
精度和召回率
准确率—测量值对标准(或已知)值的接近程度。
精度—两个测量值之间的接近程度,表示测量的可重复性或可再现性。
召回率(敏感度)—全部相关实例中被恢复的相关实例的比率。
Tp 指真正,Tn 指真负,Fp 指假正,Fn 指假负。
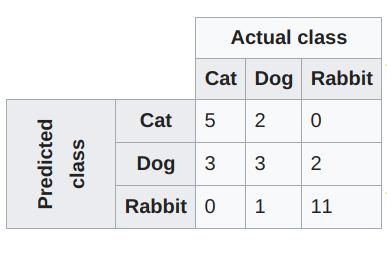
混淆矩阵—维基百科的解释是:
机器学习领域和统计分类问题中,混淆矩阵(也称为误差矩阵/error matrix)是一个算法性能的可视化表格,通常在监督学习中使用(无监督学习中混淆矩阵通常称为匹配矩阵,/matching matrix)。矩阵的每一行表示一个预测类,每一列表示一个真实类(或相反)。使用真实的名词使其易于解读,能简单地看出系统对两个类别的混淆程度(即将一个类别的物体标记为另一个)。
混淆矩阵
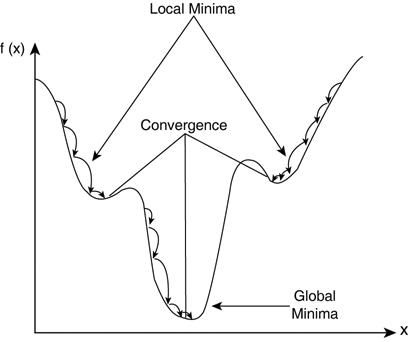
收敛—随着迭代次数增加,输出越来越接近具体的值。
正则化—用于克服过拟合问题。正则化过程中通过添加一个 L1(LASSO)或 L2(Ridge)规范到权重向量 w(通过给定算法学习到的参数)上以「惩罚」损失项:
L(损失函数)+λN(w)—这里的λ是正则项,N(w)是 L1 或 L2 规范。
归一化—数据归一化是将一个或多个属性缩放至 0 到 1 的范围的过程。当不知道数据分布或分布不是高斯分布(钟形曲线)()的时候,归一化是很有用的,可加速学习过程。
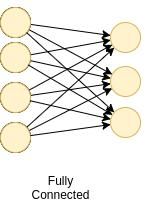
全连接层—一个层所有的节点的激活函数值作为下一层的每个节点的输入,若这对所有的层都成立,则称这些层为全连接层。
全连接层
损失函数/代价函数—损失函数计算单个训练样本的误差,代价函数是整个训练集的损失函数的平均。
「mse」—平均方差
「binary_crossentropy」—二分类对数损失(logloss)
「categorical_crossentropy」—多分类对数损失(logloss)
模型优化器—优化器是一种搜索技术,用于更新模型的权重。
SGD—随机梯度下降,支持动量算法。
RMSprop—适应性学习率优化方法,由 Geoff Hinton 提出。
Adam—适应性矩估计(Adam)并同样使用了适应性学习率。
性能指标—用于测量神经网络性能的指标,例如,准确率、损失、验证准确率、验证损失、平均绝对误差、精度、召回率和 f1 分数等等。
批大小—一次前向/反向传播中适用的样本数,批大小越大,占用的内存量越大。
训练 epochs—模型在训练数据集上重复训练的总次数。
一个 epoch= 全部训练实例的一次前向和一次反向传播。
116赞踩11评论
分享
举报
小AI咨询11-03 21:52关注
以下给出简单介绍,关于神经网络的学习方式以及深度神经网络的更多内容,欢迎到作者主页查看系列文章《神经网络与深度学习概述》。
神经网络全称人工神经网络(Artificial Neural Network,ANN),与之相对应的是生物神经网络(Biological Neural Network,BNN),将模拟生物神经网络的数学模型统称为人工神经网络模型。
生物神经系统与生物神经元
大量生物神经元的广泛、复杂连接,形成生物神经网络
实现各种智能活动
智能(intelligence)
观察、学习、理解和认识的能力
理解和各种适应性行为的能力
智能是个体有目的的行为、合理的思维、以及有效的适应环境的综合能力,也可以说是个体认识客观事物和运用知识解决问题的能力
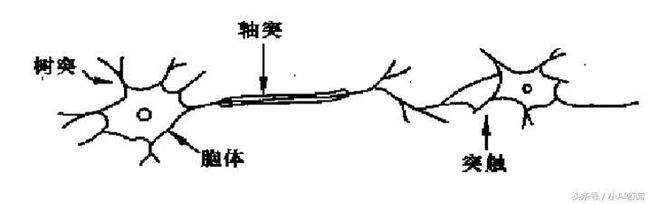
生物神经元(neuron)是基本的信息处理单元
生物神经系统
生物神经元是基本的信息处理单元。
生物神经元
树突(dendrites):接收来自外接的信息
细胞体(cell body): 神经细胞主体,信息加工
轴突(axon):细胞的输出装置,将信号向外传递,与多个神经元连接
突触 (synapsse):神经元经突触向其它神经元(胞体或树突)传递信号
生物神经元的基本特征
神经元之间彼此连接
神经元之间的连接强度决定信号传递的强弱
神经元之间的连接强度可以随训练改变:学习、遗忘、疲劳
神经网络中各神经元之间连接的强弱,按外部的激励信号做自适应变化
兴奋与抑制
信号可以起兴奋作用,也可以起抑制作用
一个神经元接受信号的累积效果(综合大小,代数和)决定该神经元的状态(兴奋、抑制)
每个神经元可以有一个“阈值”
人工神经网络的组成与结构
人工神经网络是由大量处理单元经广泛互连而组成的人工网络,用来模拟脑神经系统的结构和功能。而这些处理单元我们把它称作人工神经元。
人工神经网络可看成是以人工神经元为节点,用有向加权弧连接起来的有向图。在此有向图中,人工神经元就是对生物神经元的模拟,而有向弧则是轴突—突触—树突对的模拟。有向弧的权值表示相互连接的两个人工神经元间相互作用的强弱。
神经元及神经网络模型
人工神经网络的结构
人工神经网络中,各神经元的不同连接方式就构成了网络的不同连接模型。常见的连接模型有:
前向网络
从输入层到输出层有反馈的网络
层内有互联的网络
互联网络
人工神经网络的分类
按性能分:连续型和离散型网络,或确定型和随机型网络
按拓扑结构分:有反馈网络和无反馈网络
按学习方法分:有教师的学习网络和无教师的学习网络
按连接突触性质分:一阶线性关联网络和高阶非线性关联网络
人工神经网络的主要特征
能较好的模拟人的形象思维
具有大规模并行协同处理能力
具有较强的学习能力
具有较强的容错能力和联想能力
是一个大规模自组织、自适应的非线性动力系统