｛降维｝ ISOMAP等距特征映射 & MDS多维标度法

首发：https://zhuanlan.zhihu.com/p/60599491

---

介绍两种降维方法

镇楼_MDS: http://www.utdallas.edu/~herve/Abdi-MDS2007-pretty.pdf

镇楼_ISOMAP: http://www-clmc.usc.edu/publications/T/tenenbaum-Science2000.pdf

Multidimensional Scaling (MDS) 多维标度法

1、经典应用场景

在不知各点坐标的，仅知道各点间距离的情况下，求各点坐标。

下表是美国十个城市之间的飞行距离，我们如何在平面坐标上据此标出这10城市之间的相对位置，使之尽可能接近表中的距离数据呢？

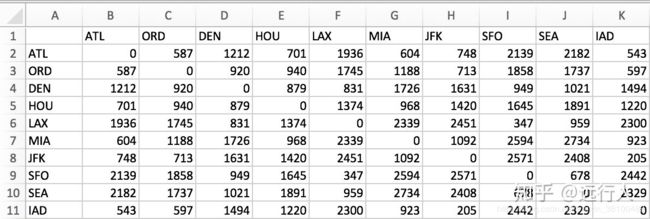
得到

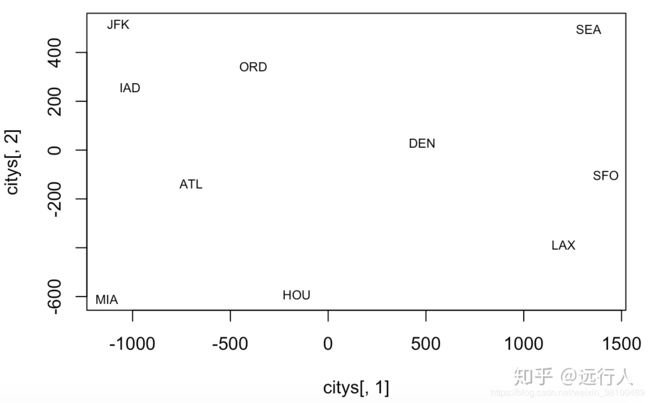
就从10维数据变成了2维，做到了降维。也恢复了10维数据内部所包含的2维数据的内涵。

经典应用是原数据都是距离的情况下，类似“距离”情况还可以是更加泛泛的“相似程度”。

2、引申应用：

经典应用中，10维数据其实就是由2维数据变化而成的。引申一下，如果假设待处理的N维数据就当做m维数据变化而成的，那么就可以通过相同方式达到降维的目的。

3、计算：

（先留空，后补全。需要的朋友可以看上面的“镇楼”。）

---

Isometric Mapping (ISOMAP) 等距特征映射

1、知识准备（跳过无妨，但挺有意思）：

流形 manifold 的理解

流形(Manifold)是局部具有欧式空间性质的空间。黎曼流形就是以光滑的方式在每一点的切空间上指定了欧式内积的微分流形。

定义看晕了就举几个例子，“球面”、“被弯曲了的平面”都是流形。下图可以看做“被弯曲了的平面”的一部分。（注意这个“被弯曲了的平面”不能折死褶，得全称“光滑”。记住这里“光滑”是个大flag，全文flag，后面会用。）

而“被弯曲了的平面”可以再被弯曲回一张平面，即从三维到二维。为什么呢？因为“被弯曲了的平面”其实是2维信息以某一形态放入了3维，在知道了该“某一形态”数据的情况下，如果已知x，就可以算出y。

而“球面”在三维欧式空间中，在知道半径的情况下，如果已知了x，就可以算出y。

即，如果已知“球面”的半径、“被弯曲了的平面”的“弯曲信息”的情况下，3维空间的他们其实都只是2维的。（这个思路也是流形学习中“降维”的基础。话糙理不糙！）

（多说一句话：这两例中2维信息对应到了3维，就是“流形”这个词的中文译者江泽涵所说“杂然赋流形”，2维的数据经过“杂然”参杂了其他数据就变成了3维或者更多维。多妙啊！！撒花撒花！！）

（再多说一句：上面说的“被弯曲了的平面”、“球面”都是2维流形，而非3维流形。）

2、isomap思路：

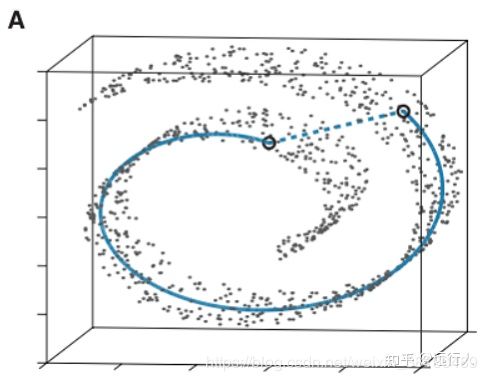
图中一个点是一个样本，样本是三个维度的，而图中的各点组成的曲面是一个流形。（图例显然是流形，就是为了讲解这事儿而特意做的，当然是啦！处理现实问题时可以假设是流形，反正难以证明是，也难以证明不是。）

而传统的PCA、LDA都不能处理这个非线性的降维问题。但由于这是个流形，如果能将该曲面以某种方式展开成为平面，那么就完成了从3维到2维的降维。后面就可以用上述MDS的方式继续做降维。

至此，该问题转化为“如何把曲面展开平面”（即“如果把流形展开”）。

以宏观视角来看，这些样本是3维的无疑；但如果以微观视角来看，由于流形各处都是“光滑”的（前文说的flag，嗯嗯，没死褶），所以只要足够小，那么就近似于平面。为了把局部微观的平面扩展到全局宏观的平面，就需要打断遥远点的联系，只保留临近点的联系。

引入图论框架，连接相邻的点构建一个连接图，被称作“邻接图”（neighborhood graph）

连接相邻的点的具体方式有二：一是最近的k个点；二是以r为半径划定一个区域（多维的），内部的就算“临近的”。

现在有了这张图，如果扔下3维空间仅看这张图，那么就是

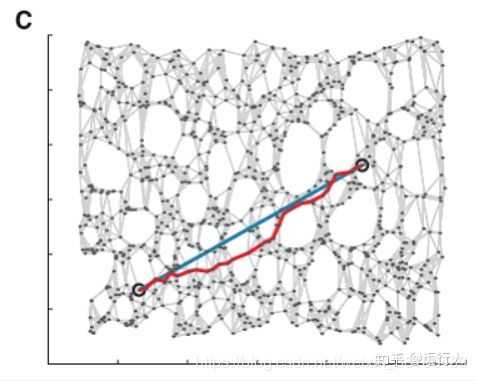
这张图就是 三维欧式空间里的二维流形 在 二维欧式空间 的近似对应。蓝线是流形真实展开后的距离；红线是用临近点的方式近似展开后的距离。二者不能完全重合，所以叫“近似”。

按论文中的表述：

后面就可以用MDS做了。

3、测地线 geodesic distance

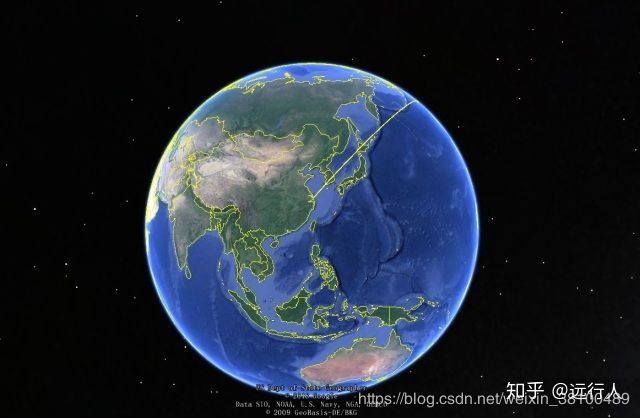
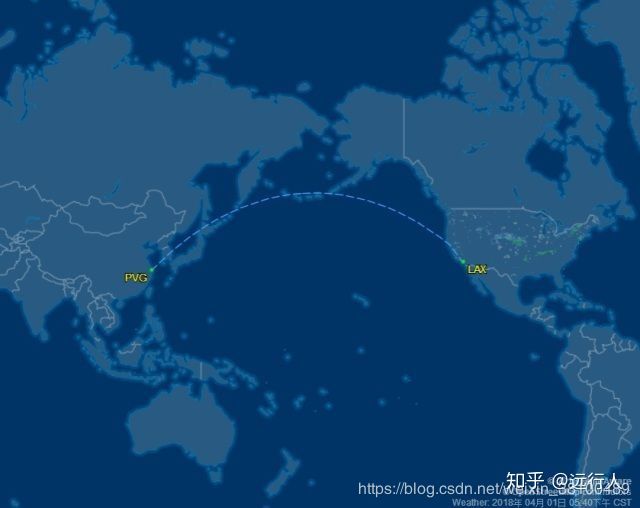
关于论文中的测地线距离的概念，可以以一个非常好的例子，（https://www.zhihu.com/question/24548348/answer/358774739 的回答真好）中美航线怎样最短，想必这样最短

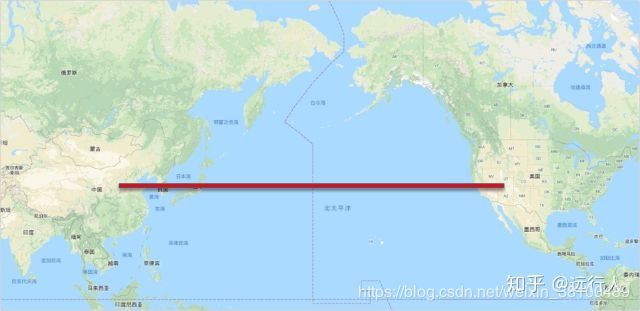
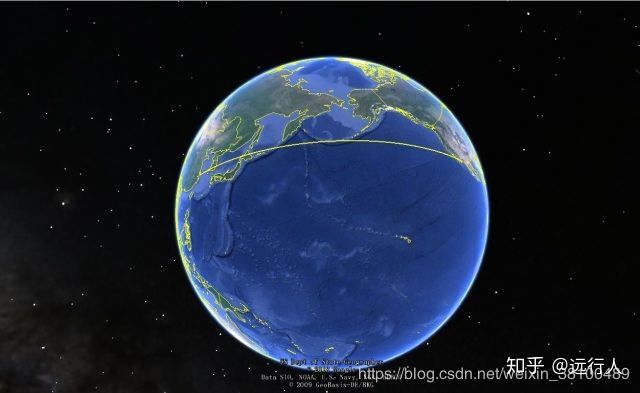
但是由于地球不是平面，所以，最短的是这样：

画在二维地图上就是

这才是实际上的最短路线，也就是“测地线 Geodesic distance”。

这时你再看图就能明白图A中蓝色虚线是三维空间中的最短连线，也就是“距离”；而在二维流形中的最短连线，也就是距离，是蓝色直线。这根蓝色直线就是图中二维流体的测地线。

首发链接：https://zhuanlan.zhihu.com/p/60599491

参考：流形学习之等距特征映射（Isomap） - wing1995 - 博客园
​

拓展阅读：有谁给解释一下流形以及流形正则化？

如果你觉得本文有些许帮助，请点赞~~~~

---

更多降维方式：降维方法小结和理解：PCA、LDA、MDS、ISOMAP、SNE、T-SNE、AutoEncoder