力扣动态规划
力扣动态规划
- 1. 斐波那契数列
- 70. 爬楼梯
- 1要求
- 2 思路
- 198. 打家劫舍
- 1要求
- 2.思路
- 213
- 1 要求
- 2.思路
- 矩阵路径
- 64. 最小路径和
- 1 要求
- 2.思路
- 62. 不同路径
- 1要求
1. 斐波那契数列
70. 爬楼梯
1要求
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
3. 1 阶 + 1 阶 + 1 阶
4. 1 阶 + 2 阶
5. 2 阶 + 1 阶
2 思路
即它的最优解可以从其子问题的最优解来有效地构建,我们可以使用动态规划来解决这一问题。
第 i 阶可以由以下两种方法得到:
在第 (i-1)(阶后向上爬一阶。
在第 (i-2)阶后向上爬 22 阶。
所以到达第 i 阶的方法总数就是到第 ((i−1) 阶和第 (i−2) 阶的方法数之和。
令 dp[i] 表示能到达第 i 阶的方法总数:
dp[i]=dp[i-1]+dp[i-2]
动态规划:
class Solution {
public int climbStairs(int n) {
if(n==1){
return 1;
}
int [] dp=new int[n+1];
dp[1]=1;
dp[2]=2;
for(int i=3;i<dp.length;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
}
斐波那契数列
class Solution {
public int climbStairs(int n) {
if(n<=2){
return n;
}
int pre1=1,pre2=2;
for(int i=2;i<n;i++){
int cur=pre1+pre2;
pre2=pre1;
pre1=cur;
}
return pre1;
}
}
198. 打家劫舍
1要求
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
2.思路
动态规划:
定义 dp 数组用来存储最大的抢劫量,其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。
由于不能抢劫邻近住户,如果抢劫了第 i -1 个住户,那么就不能再抢劫第 i 个住户,所以
class Solution {
public int rob(int[] nums) {
int curmax=0;
int premax=0;
for(int i=0;i<nums.length;i++){
int cur=Math.max(premax+nums[i],curmax);
premax=curmax;
curmax=cur;
}
return curmax;
}
}
213
1 要求
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入: [1,2,3,1]
输出: 4
解释: 你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
2.思路
前一个题可以求得最大的值,这个多了一点限制,就是不可以同时取到首尾状态的值,然后排除这两种情况。
class Solution {
public int rob(int[] nums) {
if(nums==null||nums.length==0){
return 0;
}
int n=nums.length;
if(n==1){
return nums[0];
}
return Math.max(rob(nums,0,n-2),rob(nums,1,n-1));
}
public int rob(int [] nums,int first,int last){
int curm=0;
int prem=0;
for(int i=first;i<=last;i++){
int cur=Math.max(prem+nums[i],curm);
prem=curm;
curm=cur;
}
return curm;
}
}
矩阵路径
64. 最小路径和
1 要求
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小
2.思路
在上个解法中,我们可以用一个一维数组来代替二维数组,dpdp 数组的大小和行大小相同。这是因为对于某个固定状态,只需要考虑下方和右侧的节点。首先初始化 dpdp 数组最后一个元素是右下角的元素值,然后我们向左移更新每个 dp(j)dp(j) 为:
dp(j)=\mathrm{grid}(i,j)+\min\big(dp(j),dp(j+1)\big)
dp(j)=grid(i,j)+min(dp(j),dp(j+1))
我们对于每一行都重复这个过程,然后向上一行移动,计算完成后 dp(0)dp(0) 就是最后的结果。
class Solution {
public int minPathSum(int[][] grid) {
if(grid.length==0||grid[0].length==0){
return 0;
}
int m=grid.length;
int n=grid[0].length;
int [] dp=new int[n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(j==0){
dp[j]=dp[j]; // 只能从上侧走到该位置
}else if(i==0){
dp[j]=dp[j-1]; // 只能从左侧走到该位置
}else{
dp[j]=Math.min(dp[j-1],dp[j]);
}
dp[j]+=grid[i][j];
}
}
return dp[n-1];
}
}
62. 不同路径
1要求
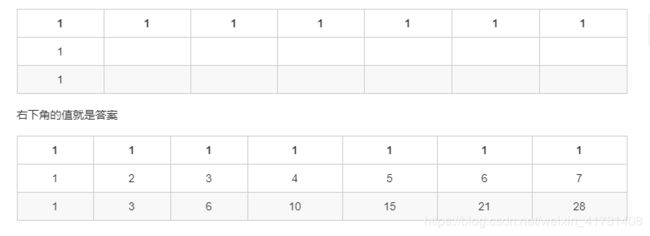
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
说明:m 和 n 的值均不超过 100。
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向右 -> 向下
- 向右 -> 向下 -> 向右
- 向下 -> 向右 -> 向右
示例 2:
class Solution {
// public int uniquePaths(int m, int n) {
// int [] dp=new int[n];
// Arrays.fill(dp,1);
// for(int i=1;i
// for(int j=1;j
// dp[j]=dp[j]+dp[j-1];
// }
// }
// return dp[n-1];
// }
public int uniquePaths(int m, int n) {
int[][] res = new int[m][n];
for (int i = 0; i < n; i++)
res[0][i] = 1;
for (int i = 0; i < m; i++)
res[i][0] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
res[i][j] = res[i - 1][j] + res[i][j - 1];
}
}
return res[m - 1][n - 1];
}
}
链接:https://leetcode-cn.com/problems/climbing-stairs
https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode%20%E9%A2%98%E8%A7%A3%20-%20%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92.md#1-%E7%88%AC%E6%A5%BC%E6%A2%AF