字节跳动专场：力扣第 197 场周赛

1、好数对的数目

1、题目描述

2、题解：

方法1：暴力法
两次循环，找满足条件的对数

class Solution:
    def numIdenticalPairs(self, nums: List[int]) -> int:
        #暴力法
        res = 0
        for i in range(len(nums)-1):
            for j in range(i+1,len(nums)):
                if nums[i] == nums[j]:
                    res += 1
        return res

方法2：哈希表法：
先建立哈希表，统计每个数出现几次；
遍历，计算好数对：对于每个单词出现的次数，计算好数对：v*(v-1)//2

class Solution:
    def numIdenticalPairs(self, nums: List[int]) -> int:
        #哈希表法
        # hashmap = {}
        hashmap = collections.defaultdict(int)
        #遍历，建立哈希表，统计每个数出现几次
        for num in nums:
            hashmap[num] += 1
        #遍历，计算好数对
        res = 0
        for key,v in hashmap.items():
            if v > 1:
                res += v*(v-1)//2
        return res

2、仅含 1 的子串数

1、题目描述：

2、题解：

方法1：从后往前遍历

class Solution:
    def numSub(self, s: str) -> int:
        x = 0
        res = 0
        for i in range(len(s) - 1,-1,-1):
            if s[i] == '0':
                x = 0
            else:
                x += 1
            res += x
        return int(res % (1e9 + 7))

方法2：双指针法

class Solution:
    def numSub(self, s: str) -> int:
        #双指针
        ln = len(s)
        left,right = 0,0
        res = 0
        while right < ln:
            if '1' not in s[right+1:]:
                if '0' not in s[left:right+1]:
                    res += sum(range(1,right-left+2))
                    left = right + 1
                    break
            if '0' not in s[left:right+1] and s[right+1] == '0':
                res += sum(range(1,right-left+2))
                left = right+1
            if left >= ln:
                break
            if s[left] == '0':
                left += 1
            right += 1
        return res %1000000007

遍历，求连续1的个数，用公式v(v+1)//2*

class Solution:
    def numSub(self, s: str) -> int:
        #双指针
        left,right = 0,1
        if not s:return 0
        n = len(s)
        res = 0
        while left < n and  right < n:
            if s[left] == '1':
                right = left + 1
                while right < n and s[right] == '1':
                    right += 1
                temp = right - left
                res += temp * (temp + 1) // 2
                left = right
            else:
                left += 1
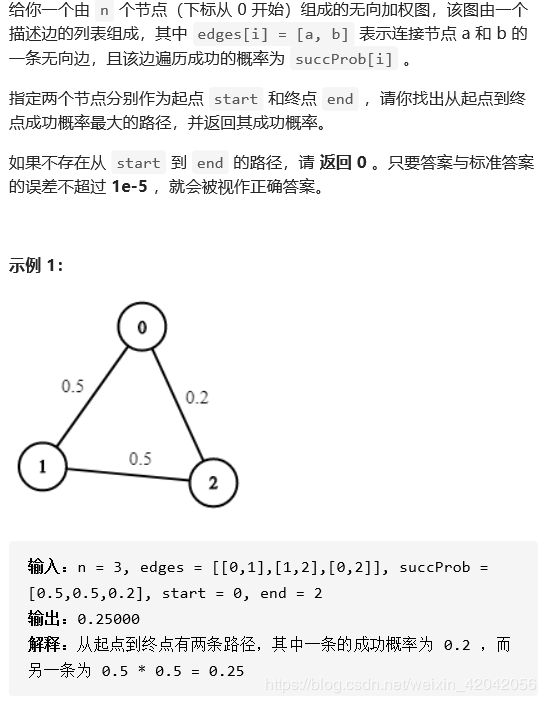
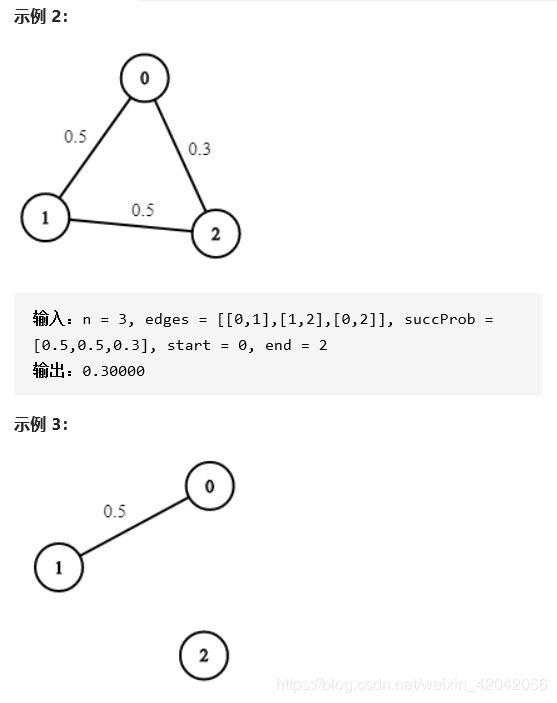
        return int(res % (1e9 + 7))

3、概率最大的路径

1、题目描述：

2、题解：

class Solution:
    def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:
        #BFS
        if not edges or not edges[0]: return 0
        # 构造节点邻接表
        from collections import defaultdict
        st_maps = defaultdict(list)
        for i, (s, e) in enumerate(edges):
            st_maps[s].append((e, succProb[i]))
            st_maps[e].append((s, succProb[i]))

        ans = 0
        queue = deque([(start, 1)])
        visited = {start: 0}
        while queue:
            # 当前节点
            cur_node, cur_prob = queue.popleft()
            for next_node, p in st_maps[cur_node]:
                # 下一个待遍历的节点
                next_prob = cur_prob * p
                if next_node == end:
                    ans = max(ans, next_prob)
                    continue

                # 剪枝和去重：如果下一个待遍历节点的概率大于ans && (该节点为遍历过 或 遍历过该节点但是上次的概率比现在小)
                if next_prob > ans and (next_node not in visited or visited[next_node] < next_prob):
                    visited[next_node] = next_prob
                    queue.append((next_node, next_prob))
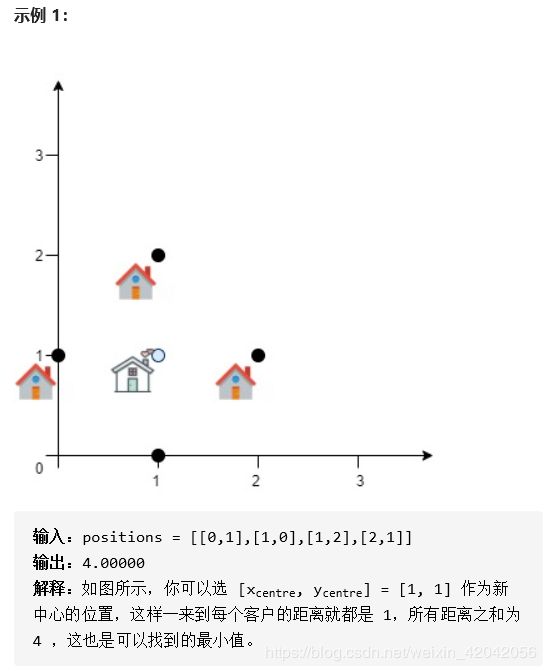
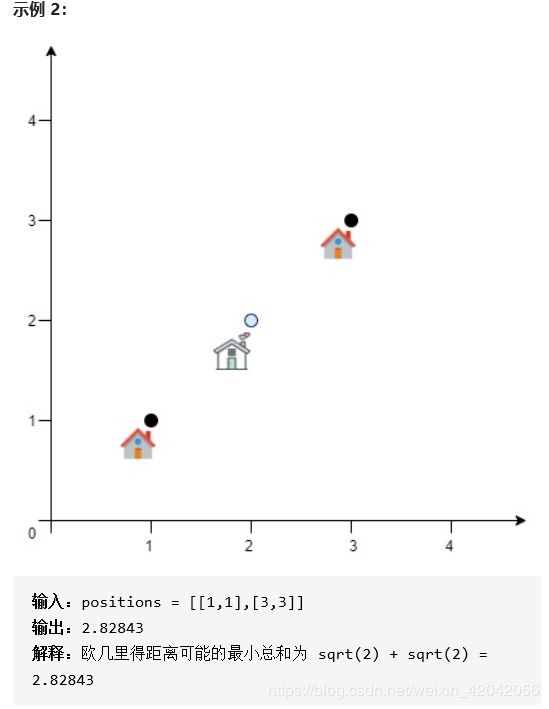
        return ans

4、服务中心的最佳位置

1、题目描述：

2、题解：

class Solution:
    def getMinDistSum(self, positions: List[List[int]]) -> float:
        # 到各点距离之和
        def dis(x, y):
            return sum([((px - x) ** 2 + (py - y) ** 2) ** 0.5 for px, py in positions])

        # 三分找最小
        def three_divide(l, r, f, eps=1e-6):
            while r - l > eps:
                m = l + (r - l) / 3
                mm = r - (r - l) / 3
                if f(m) < f(mm):
                    r = mm
                else:
                    l = m
            return (l + r) / 2

        # 左右边界
        lmin, rmax = 0, 100

        # 外层查x,x=mx时最小距离
        def xf(mx):
            # 内层查y,x=mx且y=my的距离
            def yf(my): return dis(mx, my)
            return dis(mx, three_divide(lmin, rmax, yf))

        x = three_divide(lmin, rmax, xf)
        y = three_divide(lmin, rmax, lambda my: dis(x, my))
        return dis(x, y)