深度强化学习5——Deep Q-Learning(DQN)
之前大量叙述了强化学习的基本原理,至此才开始真正的深度强化学习的部分。2013和2015年DeepMind的Deep Q Network(DQN)它用一个深度网络代表价值函数,依据强化学习中的Q-Learning,为深度网络提供目标值,对网络不断更新直至收敛。用DQN从玩各种电子游戏开始,直到训练出阿尔法狗打败了人类围棋选手。本篇文章也主要围绕DeepMind的论文Playing Atari with Deep Reinforcement Learning来讲解DQN。
Deep Q-Network(DQN)
Deep Q-Learning 算法简称DQN,DQN是在Q-Learning的基础上演变而来的,DQN对Q-Learning的修改主要有两个方面:
1)DQN利用深度卷积神经网络逼近值函数
2)DQN利用了经验回放训练强化学习的学习过程
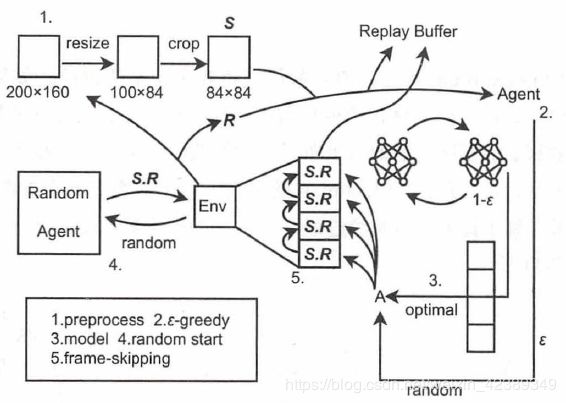
结构如下:
我们现在来具体看看这两个方面:
1)DQN的行为值函数是利用神经网络逼近,属于非线性逼近,DQN所用的网络结构是三个卷积层加两个全连接层。用公式表示的话,值函数为![]() ,此时更新网络其实就是更新参数
,此时更新网络其实就是更新参数![]() ,一旦
,一旦![]() 定了,网络参数就定了。
定了,网络参数就定了。
2)DQN最主要的特点是引入了经验回放,传统Q-Leaning 方法基于当前策略进行交互和改进,每一次模型利用交互生成的数据进行学习,学习后的样本被直接丢弃。但如果使用机器学习模型代替表格式模型后再采用这样的在线学习方法,就有可能遇到两个问题,这两个问题也都和机器学习有关:
- 交互得到的序列存在一定的相关性。交互序列中的状态行动存在着一定的相关性,而对于基于最大似然法的机器学习模型来说,我们有一个很重要的假设:训练样本是独立且来自相同分布的,一旦这个假设不成立,模型的效果就会大打折扣。而上面提到的相关性恰好打破了独立同分布的假设,那么学习得到的值函数模型可能存在很大的波动。
- 交互数据的使用效率。采用梯度下降法进行模型更新时,模型训练往往需要经过多轮迭代才能收敛。每一次迭代都需要使用一定数量的样本计算梯度, 如果每次计算的样本在计算一次梯度后就被丢弃,那么我们就需要花费更多的时间与环境交互并收集样本。
为解决以上两个问题,即将一个五元组![]() 添加到一个经验池Replay Buffer中,这些五元组之后将用来更新Q网络参数,在这里
添加到一个经验池Replay Buffer中,这些五元组之后将用来更新Q网络参数,在这里![]() 和
和![]() 都是向量的形式,动作
都是向量的形式,动作![]() 和奖励
和奖励![]() 是标量,terminal是布尔值。Replay Buffer 包含了收集样本和采样样本两个过程。收集的样本按照时间先后顺序存入结构中,如果Replay Buffer 已经存满样本,那么新的样本会将时间上最久远的样本覆盖。而对采样来说,如果每次都取出最新的样本, 那么算法就和在线学习相差不多; 一般来说,Replay Buffer 会从缓存中均匀地随机采样一批样本进行学习。这样,每次训练的样本通常来自多次交互序列,这样单一序列的波动就被减轻很多,训练效果也就更加稳定。同时,一份样本也可以被多次训练,提高了样本的利用率,相关结构如下:
是标量,terminal是布尔值。Replay Buffer 包含了收集样本和采样样本两个过程。收集的样本按照时间先后顺序存入结构中,如果Replay Buffer 已经存满样本,那么新的样本会将时间上最久远的样本覆盖。而对采样来说,如果每次都取出最新的样本, 那么算法就和在线学习相差不多; 一般来说,Replay Buffer 会从缓存中均匀地随机采样一批样本进行学习。这样,每次训练的样本通常来自多次交互序列,这样单一序列的波动就被减轻很多,训练效果也就更加稳定。同时,一份样本也可以被多次训练,提高了样本的利用率,相关结构如下:
接下来我们看看整体训练步骤:
假设迭代轮数为EPISODES,采样的序列最大长度为L,学习速率为![]() ,衰减系数为
,衰减系数为![]() ,探索率
,探索率![]() ,状态集为S,动作集为A,批量梯度下降时的batch_size = m,经验回放池最大尺寸n。
,状态集为S,动作集为A,批量梯度下降时的batch_size = m,经验回放池最大尺寸n。
1)for episode in range(EPISODES):
2)初始化状态s,在这里s为状态向量
3)for step in range(T):
a) 在这里将状态向量s输入到Q网络中,采用ϵ−greedy获得动作a;
b) 在状态s下执行当前动作a,获得下一状态![]() ,当前奖励r,是否终止状态terminal;
,当前奖励r,是否终止状态terminal;
c) 将上面获得的五元组![]() 添加到经验回放池中:
添加到经验回放池中:
A)判断若池子的大小大于m值,则从池子中批量采样并更新网络参数;
一)从经验回放池中随机采取m个样本![]() ,其中j=1,2,3....,m,计算目标值
,其中j=1,2,3....,m,计算目标值![]() :
:
![]()
二)使用均方差损失函数![]() 更新Q网络参数
更新Q网络参数
B)判断若池子大小若大于n,则从池子中取出最早加入的五元组,添加新的五元组;
d) 对状态进行更新,![]() ;
;
e) 判断terminal是否是最终状态,若是循环结束,跳转到1),若不是继续循环采样。
看完整个流程之后再来回头看经验回放的作用:我们知道在训练神经网络的时候是假设训练数据是独立同分布的,但如果你采取当前参数下的网络获得的样本来更新当前的网络参数,那么这些顺序数据之间存在很强的关联性,网络的训练会很不稳定,现在利用经验回放的方法,你在更新当前时刻参数时会随机用到不同时刻参数下获得的样本,这样样本之间的关联性相对来说比较小。直接训练Q网络的好处是,只要Q值收敛了,则每个状态对应的最大动作也就确定了,也就是确定性的策略是已经确定了。
Nature DQN
我们注意到DQN(NIPS 2013)里面,我们使用的目标Q值的计算方式:
![]()
这里目标Q值的计算使用到了当前要训练的Q网络参数来计算,而实际上,我们又希望通过![]() 来后续更新Q网络参数。这样两者循环依赖,迭代起来两者的相关性就太强了。不利于算法的收敛,因此在Nature DQN(Human-level control through deep reinforcement learning)中提出了使用两个网络 Behavior Network和Target Network:
来后续更新Q网络参数。这样两者循环依赖,迭代起来两者的相关性就太强了。不利于算法的收敛,因此在Nature DQN(Human-level control through deep reinforcement learning)中提出了使用两个网络 Behavior Network和Target Network:
(1)在训练开始时,两个模型使用完全相同的参数。
(2)在训练过程中, Behavior Network 负责与环境交互,得到交互样本。
(3)在学习过程中,由Q-Learning 得到的目标价值由Target Network 计算得到;然后用它和Behavior Network 的估计值进行比较得出目标值并更新Behavior Network。
(4)每当训练完成一定轮数的迭代, Behavior Network 模型的参数就会同步给Target Network ,这样就可以进行下一个阶段的学习。
总结
本章介绍了DeepMind提出的DQN算法和相应的改进算法Nature DQN ,把Q-learning与深度学习结合,因此有了解决大规模强化学习问题的能力,但是DQN还是存在很多问题:
1) 目标Q值的计算是否准确?全部通过max Q来计算有没有问题?
2) 随机采样的方法好吗?按道理不同样本的重要性是不一样的。
3) Q值代表状态,动作的价值,那么单独动作价值的评估会不会更准确?
第一个问题对应的改进是Double DQN, 第二个问题的改进是Prioritised Replay DQN,第三个问题的改进是Dueling DQN,这三个DQN的改进版我们在下一篇来讨论。
个人相关深度强化学习github地址:https://github.com/demomagic
PS: 如果觉得本篇本章对您有所帮助,欢迎关注、评论、赞!如果要转发请注明作者和出处
参考文献:
[1]深度强化学习(三):从Q-Learning到DQN
[2]强化学习(九)Deep Q-Learning进阶之Nature DQN