差分进化算法之Matlab实现

一、介绍
差分进化算法是模拟自然界生物种群以“优胜劣汰，适者生存”为原则的进化发展规律而形成的一种随机启发式搜索算法。其保留了基于种群的全局搜索策略，采用实数编码，基于差分的简单变异操作和一对一的竞争生存策略，比遗传算法更简单。同时，差分进化算法独特的记忆能力使其可以动态的跟踪当前的搜索情况，及时调整搜索测量，因此具有较强的全局收敛能力。
目前为止，差分进化算法已经成为一种求解非线性，不可微，多极值和高维复杂函数的一种极其有效的方法。
在优化设计中，差分进化算法与传统的算法相比，具有以下特点：
1.差分进化算法从一个群体即多个点而不是从一个点开始搜索，这也是算法能够以较大的概率找到整体最优解的原因。
2.算法的进化准则是基于适应性信息的，不需要其他的辅助性信息，如要求函数可导，连续等。
3. 差分进化算法具有内在的并行性，适用于大规模并行分布处理，减小时间成本开销。
但缺点为：
1.算法后期个体之间的差异性减小，收敛速度慢，易陷入局部最优。
2.没有利用个体的先验知识，可能较多的迭代次数才能收敛到全局最优
算法框架：

(1)群体初始化
在n维空间里随机产生满足约束条件的M个个体
$$x_{ij}(0)=x_{i{j}_{min}}+(x_{i{j}_{max}}-x_{i{j}_{min}})\ast rand(0,1)$$
其中，$x_{i{j}_{max}},x_{i{j}_{min}}$表示第$j$个染色体的上下界。
(2) 变异
从群体中随机选择三个个体$x_{p1},x_{p2},x_{p3}$且要求$i̸=p1̸=p2̸=p3$,则：
$$h_{ij}(t+1)=x_{p1j}(t)+F\ast (x_{p2j}(t)-x_{p3j}(t))$$
如果没有局部优化的问题，变异操作为：
$$h_{ij}(t+1)=x_{bj}(t)+F\ast (x_{p2j}(t)-x_{p3j}(t))$$
其中，$x_{p2j}(t)-x_{p3j}(t)$为差异化向量，是差分进化算法的关键；F为变异因子；P1，P2,P3为随机整数，表示个体在种群中的序号；$x_{bj}$是当前种群中最好的个体，这一步借鉴了当前种群中最好的个体信息，可以大大加快收敛速度
(3) 交叉
交叉操作可以增加群体的多样性
$$v_{ij}(t+1)=\{\begin{array}{c}{h}_{ij}(t+1),rand{l}_{ij}\le CR\\ hxij(t),rand{l}_{ij}>CR\end{array}$$
CR为交叉因子。
(4) 选择操作
为了确定$x_i(t+1)$是否成为下一代的成员，我们需要对目标向量和当前的向量的适应度值进行比较，具体由适应度函数决定：
$$x_i(t+1)=\{\begin{array}{c}{v}_i(t+1),f(v_{i1}(t+1),...v_{in}(t+1))<f(x_{i1}(t),...,x_{in}(t))\\ x_i(t+1),f(v_{i1}(t+1),...v_{in}(t+1))\ge f(x_{i1}(t),...,x_{in}(t))\end{array}$$
通过反复执行步骤(2)到(4),直至达到最大的迭代次数。
二、参数设置
1.变异因子F
变异因子是控制种群多样性和收敛性的重要参数，当F值较小时，种群之间的差异度小，容易使得种群过早的收敛于局部最小值，当F过大时，容易跳出局部最优解，但是收敛速度会减慢。F一般在[0,2]之间取值。
2.交叉因子CR
交叉因子可以控制个体参数的各维对交叉的参与程度，全局搜索和局部搜索能力的平衡。CR越小，种群多样性减小，容易收敛于局部最优解。CR越大，收敛速度变快，但过大，扰动大于群体差异度时，会导致收敛变慢。CR一般取[0,1]之间。
3.群体规模Size
Size一般为5D和10D之间，D时求解的维度。Size越大，获得最优解的概率越大，但计算时间增长。
4.迭代次数G
G 一般作为近化过程的终止条件，G越大，最优解越精准。当然终止条件也可以由适应度函数给出。
三、matlab代码
以函数
$$f(x,y)=-20e^{-0.2\sqrt{（x^2+y^2）/2}}-e^{(cos2\pi x+cos2\pi y)/2}+e$$为例
三维图为：

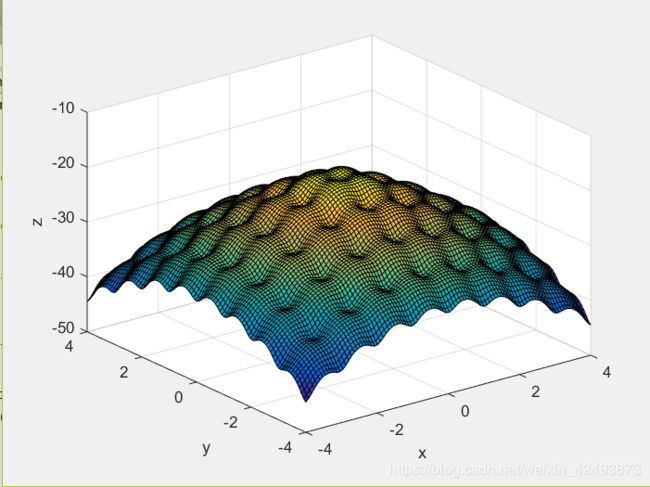
可见该函数是多极值的。函数全局最优解为max(max(f(x,y)))=-19.2926，使用一般的算法，极易陷入局部的最优解。
使用差分进化算法，结果为-19.2523,与真实值十分的接近。
适应度函数变化曲线为：

matlab代码为：

% clear all;
% close all;
%
size=50;%群体个数
Codel=2;%所求的变量个数
 MinX(1)=-5;%未知量范围
 MinX(2)=-5;
 MaxX(1)=5;
 MaxX(2)=5;
 G=200;%迭代次数
 F=1.2;%变异因子[0 2]
 cr=0.8;%交叉因子[0.6 0.9]
 %初始化种群
 for i=1:1:Codel
 P(:,i)=MinX(i)+(MaxX(i)-MinX(i))*rand(size,1);    
 end
 
 Best=P(1,:);%全局最优个体 之后不断更新
  for i=2:size
     if(fun_DE(P(i,1),P(i,2))>fun_DE(Best(1),Best(2)))
         Best=P(i,:);
     end
  end
  fi=fun_DE(Best(1),Best(2));%不是C语言 一定要记得给初始变量否则程序跑飞
  %%进入循环直到满足精度要求或者迭代次数达到
  for Kg=1:1:G
     time(Kg)=Kg;
     %第二步 变异
      for i=1:size
          r1=1;r2=1;r3=1;r4=1;%使得个体满足变异条件
          while(r1==r2||r1==r3||r1==r4||r2==r3||r2==r4||r3==r4||r1==i||r2==i||r3==i||r4==i)
            r1=ceil(size*rand(1));%大小匹配 
            r2=ceil(size*rand(1));
            r3=ceil(size*rand(1));
            r4=ceil(size*rand(1));
          end
          h(i,:)=P(r1,:)+F*(P(r2,:)-P(r3,:));
          %h(i,:)=Best+F*(P(r2,:)-P(r3,:));
          for j=1:Codel %检查是否越界
              if(h(i,j)MaxX(j)) 
                  h(i,j)=MaxX(j);
              end
          end
          %交叉
        for j=1:Codel
        temper=rand(1);
        if(temperfun_DE(P(i,1),P(i,2)))
            P(i,:)=v(i,:);
        end
        if(fun_DE(P(i,1),P(i,2))>fi)
            fi=fun_DE(P(i,1),P(i,2));
            Best=P(i,:);
        end
      end
      Best_f(Kg)=fun_DE(P(i,1),P(i,2));
      
  end
  fprintf('最优解结果为%f,%f',Best(1),Best(2));
   fprintf('最大函数值为%f',Best_f(Kg));
   plot(time,Best_f(time));

适应度函数

function J=fun_DE(x1,x2)
% J=100*(x1^2-x2)^2+(1-x1)^2;
J=-20*exp((0.2*sqrt((x1^2+x2^2)/2)))-exp((cos(2*pi*x1)+cos(2*pi*x2))/2)+exp(1);
end