C-Cover the Tree(2020牛客暑期多校训练营(第二场))(找规律)
C-Cover the Tree(2020牛客暑期多校训练营(第二场))(找规律)
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
Special Judge, 64bit IO Format: %lld
链接:https://ac.nowcoder.com/acm/contest/5667/C
来源:牛客网
题目描述
Given an unrooted tree, you should choose the minimum number of chains that all edges in the tree are covered by at least one chain. Print the minimum number and one solution. If there are multiple solutions, print any of them.
输入描述:
The first line contains one integer n ( 1 ≤ n ≤ 2 × 105 ) n (1≤n≤2×105) n(1≤n≤2×105), denoting the size of the tree.
Following n − 1 n−1 n−1 lines each contains two integers u , v ( 1 ≤ u < v ≤ n ) u,v (1≤u
It’s guaranteed that the given graph forms a tree.
输出描述:
The first line contains one integer k k k, denoting the minimum number of chains to cover all edges.
Following k k k lines each contains two integers u , v ( 1 ≤ u , v ≤ n ) u,v (1≤u,v≤n) u,v(1≤u,v≤n), denoting a chain you have chosen. Here u = v u=v u=v is permitted, which covers no edge.
输入
5
1 2
1 3
2 4
2 5
输出
2
2 3
4 5
题解
题意是给你一颗树,让你选出其中的一些链,使得这些链能够覆盖树上的所有的边,链与链之间可以彼此交叉重叠。
首先我们选出的每条链的两端一定都是叶子节点,如果不是叶子节点的话一定可以使链条继续向外扩展延长以便覆盖更多的边。所以问题就变成了如何选出多干个叶子节点对,使得他们的路径覆盖所有的边,叶子节点可以重复选择,路径也可以彼此交叉重叠。
假设有如下树:
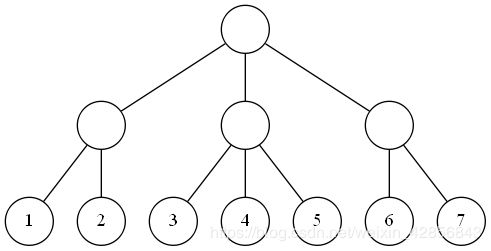
随机选出一个边a,a的儿子节点覆盖的叶子节点区间为[L, R]。
当 R ≤ s 2 R≤\frac{s}{2} R≤2s时,这条边会被 l R → l R + s 2 l_{R}\to l_{R+\frac{s}{2}} lR→lR+2s覆盖。
例如:
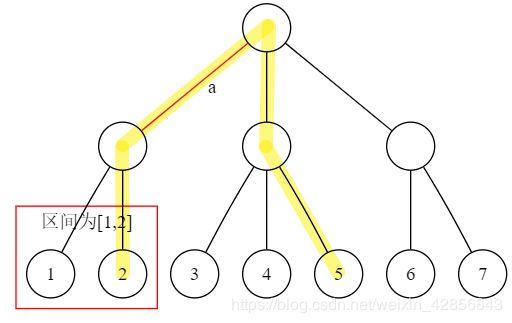
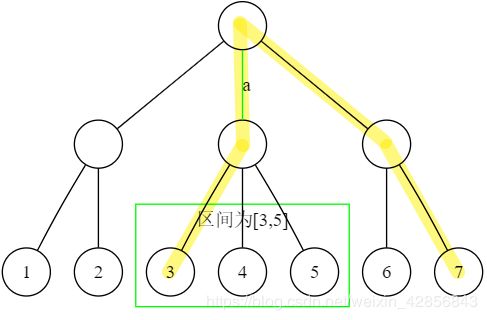
否则当 L > s 2 L>\frac{s}{2} L>2s时,这条边会被 l L − s 2 → l L l_{L-\frac{s}{2}}\to l_L lL−2s→lL覆盖。
例如:
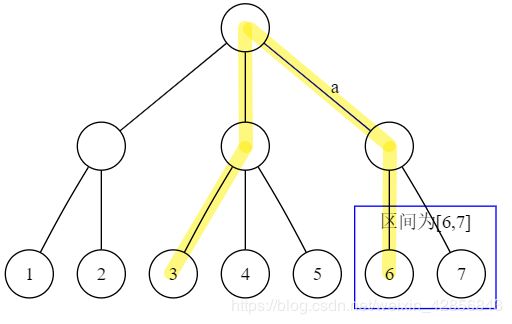
否则因为根节点度数不为1,所以 L ≠ 1 , R ≠ s L \not= 1,R\not= s L=1,R=s中必有一个是满足的,如果 L ≠ 1 L\not=1 L=1则这条边会被 l 1 → l s 2 + 1 l_1\to l_{\frac{s}{2}+1} l1→l2s+1覆盖,如果 R ≠ s R\not=s R=s则这条边会被 l s 2 → l s l_{\frac{s}{2}}\to l_s l2s→ls覆盖。
例如被 l 1 → l s 2 + 1 l_1\to l_{\frac{s}{2}+1} l1→l2s+1覆盖:
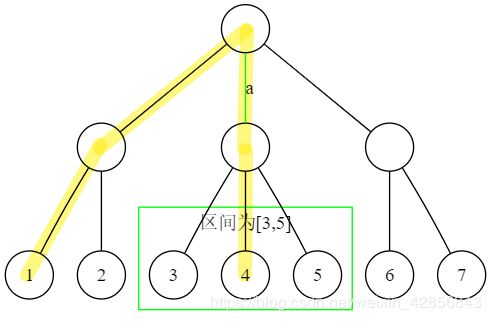
或者被 l s 2 → l s l_{\frac{s}{2}}\to l_s l2s→ls覆盖:
代码
#include 