集成树之三：GBDT

GBDT(Gradient Boosting Decision Tree)是目前工业和各种竞赛中非常抢手的模型，性能表现出色，特别是XgBoost，LightGBM推出后，模型性能和运行效率进一步提升，了解XgBoost模型，先整理一下GBDT吧。

GBDT概述

GBDT模型是一个集成模型，基分类器采用CART，集成方式为Gradient Boosting。

CART

CART是一个分类回归二叉决策树，构建一棵二叉树，主要涉及到一下一个问题：

• 怎么分裂一个特征？
• 怎么选择最佳分裂特征？
• 确定分裂的停止条件？
• 决策树的优化：剪枝方法？

因为CART是一棵二叉树，所以在分裂特征时与 ID3、C4.5有区别。
CART在分类时采用最小平方误差来选择最优切分特征和切分点。

Boosting

Boosting是一种模型的组合方式，我们熟悉的AdaBoost就是一种Boosting的组合方式。和随机森林并行训练不同的决策树最后组合所有树的bagging方式不同，Boosting是一种递进的组合方式，每一个新的分类器都在前一个分类器的预测结果上改进，所以说boosting是减少bias而bagging是减少variance的模型组合方式。

Gradient Boosting

GBDT和AdaBoost模型都可以表示成：
$$F(x)=\sum _{m=1}^M{\gamma }_m{h}_m(x)$$
的形式，只是AdaBoost在训练完一个$h_m$后会重新赋值样本的权重：分类错误的样本的权重会增大而分类正确的样本的权重则会减小。这样在训练$h_{m+1}$时会侧重对错误样本的训练，以达到模型性能的提升，但是AdaBoost模型每个基分类器的损失函数优化目标是相同的且独立的，都是最优化当前样本（样本权重）的指数损失。

GBTD虽然也是一个加性模型，但其是通过不断迭代拟合样本真实值与当前分类器的残差$y-{\hat{y}}_{h_{m-1}}$来逼近真实值的，按照这个思路，第$m$个基分类器的预测结果为：
$$F_m(x)=F_{m-1}(x)+{\gamma }_m{h}_m(x)$$
而$h_m(x)$的优化目标就是最小化当前预测结果$F_{m-1}(x_i)+h(x_i)$和$y_i$之间的差距。
$$h_m={\mathrm{argmin}}_h\sum _{i=1}^{n}L(y_i,F_{m-1}(x_i)+h(x_i))$$

下面是GDBT的一个简单例子：判断用户是否会喜欢电脑游戏，特征有年龄，性别和职业。需要注意的是，GBDT无论是用于分类和回归，采用的都是回归树，分类问题最终是将拟合值转换为概率来进行分类的。

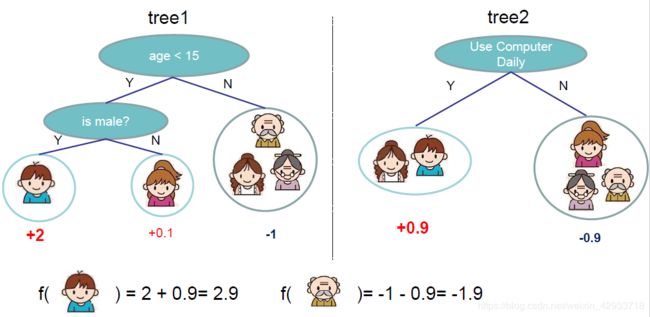
在上图中,每个用户的最后的拟合值为两棵树的结果相加。

模型公式推导

Gradient Boosting是Friedman提出的一套框架。其思想类似于数值优化中梯度下降求参方法，参数沿着梯度的负方向以小步长前进，最终逐步逼近参数的局部最优解。在GB中模型每次拟合残差，逐步逼近最终结果。

框架

在GB "greedy-stagewise"的思想中，每个stage需要最小化残差的误差，即：
$$h_m={\mathrm{argmin}}_h\sum _{i=1}^{n}L(y_i,F_m)$$
而
$$F_m(x)=F_{m-1}(x)+{\gamma }_m{h}_m(x)$$
所以，每个stage的优化的目标为：
$$h_m={\mathrm{argmin}}_h\sum _{i=1}^{n}L(y_i,F_{m-1}(x_i)+{\gamma }_{m}h(x_i))$$该函数比较难求解，类似于梯度下降方法，给定$F_{m-1}(x_i)$的一个近似解，${\gamma }_m{h}_m(x)$可以看做$F_{m-1}(x_i)$逼近$F_m(x_i)$的步长和方向。所以：
$$F_m(x)=F_{m-1}-{\gamma }_m[\frac{\partial L(y_i,F_m(x_i))}{\partial F_m(x_i)}{]}_{F_m(x)=F_{m-1}(x)}$$

$${\gamma }_m={\mathrm{argmin}}_{\gamma }\sum _{i=1}^{n}L(y_i,F_{m-1}-\gamma [\frac{\partial L(y_i,F_m(x_i))}{\partial F_m(x_i)}{]}_{F_m(x)=F_{m-1}(x)}$$

框架扩展

上一部分的GB框架可以搭配不同的损失函数来解决不同的问题：

least-squares regression

least absolute deviation regression

M_Regression

Two-class logistic regression and classificaiton

二分类时，如果采用类似于逻辑回归的对数似然损失函数：
$$L(y,f(x))=log(1+exp(-yf(x)))$$
其中$y\in \{-1,1\}$，$f(x)=log[\frac{Pr(y=1|x)}{Pr(y=-1|x)}]$, $f(x)$是一个对数几率，当样本为正的概率大于样本为负的概率时，$f(x)$函数值大于0，否则小于0。

此时负梯度误差为：
$$r_{ti}=-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}{]}_{f(x)=f_{t-1}(x)}=y_i/(1+exp(y_{i}f(x_i)))$$

而各个节点最优的拟合值为使损失函数最优解：
$$c_{tj}={\mathrm{argmin}}_c\sum _{x_i\in R_{tj}}log(1+exp(-y_i(f_{t-1}(x_i)+c)))$$

上式没有解析解，比较难优化，采用近似值（说是牛顿迭代法，但还不懂）：
$$c_{tj}=\sum _{x_i\in R_{tj}}{r}_{ti}/\sum _{x_i\in R_{tj}}|r_{ti}|(1-|r_{ti}|)$$

将拟合值转化为概率：
$p_{+}(x)=1/(1+e^{-f(x)})$， $p_{-}(x)=1/(1+e^{f(x)})$

正则项

$$F_m(x)=F_{m-1}(x)+v{\gamma }_m{h}_m(x)$$
给learning rate ${\gamma }_m$添加了一个正则项$v$

python实现

待写

参考文献

1. Friedman J H . Greedy Function Approximation: A Gradient Boosting Machine[J]. The Annals of Statistics, 2001, 29(5):1189-1232.
2. sklearn toturial classifier
3. sklearn toturial regressor
4. GBDT分类的原理及Python实现