变分贝叶斯学习记录
一、基础知识
1.为什么要变分贝叶斯?
这是由于传统贝叶斯算法中的后验概率(Posterior) P ( Z ∣ X ) P(Z|X) P(Z∣X)难以求解(其中 X X X为已知的观测数据, Z Z Z为隐变量),因此,通过变分贝叶斯的方法,寻找一个近似后验概率的概率向量,以代替传统方法中的难以求解的后验概率。后文中,在正式介绍变分贝叶斯之前,我们先来介绍一下EM算法及隐变量的含义。
2. EM算法都干了些啥?
我们先以混合高斯模型(GMM)为例,来解释一下EM(Expectation-Maximization Algorithm)算法:
假设我手头有一些东北人的身高的数据,又知道身高的概率模型是高斯分布,那么利用极大化似然函数的方法可以估计出高斯分布的两个参数,均值和方差。这是概率论课本上的极大似然估计,如下图所示:

然而现在我面临的是这种情况,我手上的数据是四川人和东北人的身高合集,然而对于其中具体的每一个数据,并没有标定出它来自 “东北人”还是“四川人”。如果把这个数据集的概率密度画出来,就是两个正态分布的叠加:
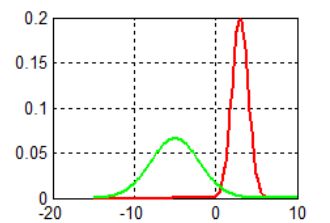
叠加以后的图片没有画,可以自己脑补一下。叠加后是一个双峰的概率密度函数,这个双峰的概率密度函数是有模型的,称作高斯混合模型(GMM),写作:

而对GMM模型进行参数估计时,这里面既要估计每个高斯分布的均值和方差,又要估计样本来源于哪一个高斯分布,此时就要用EM算法,即:

EM算法适用于带有隐变量的概率模型的估计,而关于EM算法的详细原理,这里不叙述。
3. 解释一下“隐变量Z”:
说了半天,那究竟什么是隐变量呢?隐变量就是观测不到的变量,对于上面的四川人和东北人的例子,对每一个身高而言,它来自四川还是东北,就是一个隐变量。若用 Z = 0 Z=0 Z=0或 Z = 1 Z=1 Z=1标记样本来自哪个总体,则Z就是隐变量。
(值得一提的是,隐变量Z=0 or Z=1 也可看成分类,因此,变分贝叶斯也可以做分类算法)
二、变分贝叶斯推导原理
1.明确任务
回到最开始的初衷,引入变分贝叶斯方法是由于传统贝叶斯算法中的后验概率(Posterior) P ( Z ∣ X ) P(Z|X) P(Z∣X)难以求解(其中 X X X为已知的观测数据, Z Z Z为隐变量),因此,通过变分贝叶斯的方法,寻找一个近似后验概率的概率向量,以代替传统方法中的难以求解的后验概率。
由于 P ( Z ∣ X ) P(Z|X) P(Z∣X)显然只是变量 Z Z Z的函数与 X X X无关(因为作为条件的变量都是已知的),故用以近似 P ( Z ∣ X ) P(Z|X) P(Z∣X)的概率向量可用一个关于变量 Z Z Z的函数来表示来表示,即 Q ( Z ) Q(Z) Q(Z)。
因此,我们的任务是:
寻找一个 Q ( Z ) Q(Z) Q(Z),使得他近似等价于后验概率 P ( Z ∣ X ) P(Z|X) P(Z∣X)
故有如下推导:

即: l o g P ( X ) = L ( Q ( Z ) ) + K L ( Q ( Z ) ∣ ∣ P ( Z ∣ X ) ) logP(X)=L(Q(Z))+KL(Q(Z)||P(Z|X)) logP(X)=L(Q(Z))+KL(Q(Z)∣∣P(Z∣X))
简写为: l o g P ( X ) = L ( Q ) + K L ( Q ∣ ∣ P ) logP(X)=L(Q)+KL(Q||P) logP(X)=L(Q)+KL(Q∣∣P)
2.优化目标
其中, K L ( Q ( Z ) ∣ ∣ P ( Z ∣ X ) ) KL(Q(Z)||P(Z|X)) KL(Q(Z)∣∣P(Z∣X))表示KL-散度,在信息论中接触过这个变量,其作用时用来衡量两个概率向量有多大差异。 K L ( Q ∣ ∣ P ) KL(Q||P) KL(Q∣∣P)越大,就说明Q与P之间的差异性越大,即: Q ( Z ) Q(Z) Q(Z)对 P ( Z ∣ X ) P(Z|X) P(Z∣X)的近似程度越差,因此,我们的目的是最小化 K L ( Q ∣ ∣ P ) KL(Q||P) KL(Q∣∣P),即:
m i n K L ( Q ∣ ∣ P ) \begin{aligned} minKL(Q||P) \end{aligned} minKL(Q∣∣P)
再看上面的推导,由于 X X X是已知的观测量,因此 l o g P ( X ) logP(X) logP(X)是常数,固定值。所以,最小化 K L ( Q ∣ ∣ P ) KL(Q||P) KL(Q∣∣P)可以等价于最大化 L ( Q ) L(Q) L(Q),即:
m a x L ( Q ) \begin{aligned} max L(Q) \end{aligned} maxL(Q)
由于 K L ( Q ∣ ∣ P ) ≥ 0 KL(Q||P)\geq0 KL(Q∣∣P)≥0,故:
l o g P ( X ) ) ≥ L ( Q ) \begin{aligned} logP(X))\geq L(Q) \end{aligned} logP(X))≥L(Q)
所以 L ( Q ) L(Q) L(Q)可以看成是 l o g P ( X ) logP(X) logP(X)的下界,通常称为:ELOB(Evidence Lower Bound)。也就是我们通过最大化对数数似然函数logP(X)的下界来逼近对数似然函数的logP(X)。用一个图来说明 l o g P ( X ) logP(X) logP(X)、 L ( Q ) L(Q) L(Q)、 K L ( Q ∣ ∣ P ) KL(Q||P) KL(Q∣∣P)这三者的关系:

3.求解过程
m a x L ( Q ) \begin{aligned} max L(Q) \end{aligned} maxL(Q)
其中,
L ( Q ) = ∫ Q ( Z ) l o g P ( Z , X ) d Z − ∫ Q ( Z ) l o g Q ( Z ) d Z \begin{aligned} L(Q)=\int Q(Z)logP(Z,X)dZ-\int Q(Z)logQ(Z)dZ \end{aligned} L(Q)=∫Q(Z)logP(Z,X)dZ−∫Q(Z)logQ(Z)dZ
求解上述优化目标的方法如下:
(1)假设qi(Zi)分布之间都是独立的(平均场理论的假设前提)即:
Q ( Z ) = ∏ i Q ( z i ) \begin{aligned} Q(Z)=\prod_{i}Q(z_i) \end{aligned} Q(Z)=i∏Q(zi)
d Z = ∏ j d z j \begin{aligned} dZ=\prod_{j}dz_j \end{aligned} dZ=j∏dzj
将上式带入 L ( Q ) L(Q) L(Q),故有:
∫ Q ( Z ) l o g P ( Z , X ) d Z = ∫ ∏ i Q ( z i ) l o g P ( Z , X ) d Z = ∫ Q ( z j ) ( ∏ i : i ≠ j Q ( z i ) l o g P ( Z , X ) d z i ) d z j = ∫ Q ( z j ) E i ≠ j [ l o g P ( Z , X ) ] d z j = ∫ Q ( z j ) l o g { e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) } d z j = ∫ Q ( z j ) l o g e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) ∫ e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) d z j − C = ∫ Q ( z j ) l o g Q ∗ ( z j ) d z j − C \begin{aligned} \int Q(Z) logP(Z,X)dZ &= \int \prod_i Q(z_i) logP(Z,X)dZ\\&=\int Q(z_j) \bigg (\prod_{i:i\neq j} Q(z_i) logP(Z,X)dz_i \bigg )dz_j \\&=\int Q(z_j) E_{i\neq j}[logP(Z,X)] dz_j \\&= \int Q(z_j)log \big \{exp( E_{i\neq j}[logP(Z,X)])\big \} dz_j \\&=\int Q(z_j)log\frac{exp(E_{i\neq j}[logP(Z,X)])}{\int exp(E_{i\neq j}[logP(Z,X)])} dz_j - C\\&= \int Q(z_j)logQ^*(z_j) dz_j - C \end{aligned} ∫Q(Z)logP(Z,X)dZ=∫i∏Q(zi)logP(Z,X)dZ=∫Q(zj)(i:i=j∏Q(zi)logP(Z,X)dzi)dzj=∫Q(zj)Ei=j[logP(Z,X)]dzj=∫Q(zj)log{exp(Ei=j[logP(Z,X)])}dzj=∫Q(zj)log∫exp(Ei=j[logP(Z,X)])exp(Ei=j[logP(Z,X)])dzj−C=∫Q(zj)logQ∗(zj)dzj−C
及:
∫ Q ( Z ) l o g Q ( Z ) d Z = ∫ ∏ i Q ( z i ) l o g ∏ j Q ( z j ) d Z = ∫ ∏ i Q ( z i ) ∑ j l o g Q ( z j ) d Z = ∑ j ∫ ∏ i Q ( z i ) l o g Q ( z j ) d Z = ∑ j ∫ Q ( z j ) l o g Q ( z j ) d z j ∫ ∏ i : i ≠ j Q ( z i ) d z i = ∑ j ∫ Q ( z j ) l o g Q ( z j ) d z j \begin{aligned} \int Q(Z) logQ(Z) dZ &= \int \prod_i Q(z_i)log\prod_j Q(z_j) dZ \\&= \int \prod_i Q(z_i)\sum_j log Q(z_j) dZ \\&= \sum_j \int \prod_i Q(z_i)log Q(z_j) dZ \\&= \sum_j \int Q(z_j)log Q(z_j)dz_j \int \prod_{i: i\neq j} Q(z_i) dz_i \\&= \sum_j \int Q(z_j)log Q(z_j)dz_j \end{aligned} ∫Q(Z)logQ(Z)dZ=∫i∏Q(zi)logj∏Q(zj)dZ=∫i∏Q(zi)j∑logQ(zj)dZ=j∑∫i∏Q(zi)logQ(zj)dZ=j∑∫Q(zj)logQ(zj)dzj∫i:i=j∏Q(zi)dzi=j∑∫Q(zj)logQ(zj)dzj
推导解释:
(1)由于 ∫ Q ( z i ) d z i = 1 \int Q(z_i)dz_i=1 ∫Q(zi)dzi=1,所以 ∫ ∏ i : i ≠ j Q ( z i ) d z i = ∏ i : i ≠ j ∫ Q ( z i ) d z i = 1 \int \prod_{i: i\neq j} Q(z_i) dz_i=\prod_{i: i\neq j} \int Q(z_i) dz_i=1 ∫∏i:i=jQ(zi)dzi=∏i:i=j∫Q(zi)dzi=1
(2)上述其实就是内层先对 i ≠ j i\neq j i=j的那些积分,然后外层再单独对 i = j i=j i=j的那一个积分,所以, L ( Q ) L(Q) L(Q)才有那种形式。
综上,可以得到 L ( Q ) L(Q) L(Q)为:
L ( Q ) = ∫ Q ( z j ) l o g Q ∗ ( z j ) d z j − ∑ j ∫ Q ( z j ) l o g Q ( z j ) d z j − C = ∫ Q ( z j ) l o g Q ∗ ( z j ) Q ( z j ) d z j − ∑ i : i ≠ j ∫ Q ( z i ) l o g Q ( z i ) d z i − C = − K L ( Q ( z j ) ∣ ∣ Q ∗ ( z j ) ) + ∏ i : i ≠ j H ( Q ( z i ) ) − C \begin{aligned} L(Q) &= \int Q(z_j)logQ^*(z_j) dz_j - \sum_j\int Q(z_j)log Q(z_j)dz_j - C \\&=\int Q(z_j)\frac{logQ^*(z_j)}{ Q(z_j)} dz_j -\sum_{i:i \neq j} \int Q(z_i)log Q(z_i)dz_i - C \\&= -KL(Q(z_j)||Q^*(z_j)) + \prod_{i:i\neq j}H(Q(z_i)) - C \end{aligned} L(Q)=∫Q(zj)logQ∗(zj)dzj−j∑∫Q(zj)logQ(zj)dzj−C=∫Q(zj)Q(zj)logQ∗(zj)dzj−i:i=j∑∫Q(zi)logQ(zi)dzi−C=−KL(Q(zj)∣∣Q∗(zj))+i:i=j∏H(Q(zi))−C
其中, H ( Q ( z i ) ) = − ∫ Q ( z i ) l o g Q ( z i ) d z i H(Q(z_i)) = -\int Q(z_i) logQ(z_i)dz_i H(Q(zi))=−∫Q(zi)logQ(zi)dzi为信息熵。由于信息熵非负,且KL散度也非负,故,若要 L ( Q ) L(Q) L(Q)最大,便需要KL散度为0,即:
− K L ( Q ( z j ) ∣ ∣ Q ∗ ( z j ) ) = 0 \begin{aligned} -KL(Q(z_j)||Q^*(z_j))=0 \end{aligned} −KL(Q(zj)∣∣Q∗(zj))=0
解得:
Q ( z j ) = Q ∗ ( z j ) = 1 C 0 e x p ( E i ≠ j [ l o g P ( Z , X ) ] ) \begin{aligned} Q(z_j) = Q^*(z_j) = \frac{1}{C_0}exp(E_{i\neq j}[logP(Z,X)]) \end{aligned} Q(zj)=Q∗(zj)=C01exp(Ei=j[logP(Z,X)])
其中, C 0 C_0 C0为常数。
至此,就得到了 Q ( Z ) Q(Z) Q(Z)的分布形式,也就达到了我们的初衷:寻到并顺利地得到了一个用以近似 P ( X ∣ Z ) P(X|Z) P(X∣Z)的 Q ( Z ) Q(Z) Q(Z)。
三、困惑与记录
1. 推导的疑问
因为下是推导:
所以推导时,有:图中上式到下式的过度

2. 为什么会有迭代?
不断地迭代更新q,并将刚刚计算得到的结果代入下一次计算中,一次比一次更好,因此,才会有迭代收敛一说!(感谢徐亦达老师在youtu上精彩且透彻的视频讲解!)
3. 例子记录


4. 变分贝叶斯与EM算法的区别
EM算法是叠代并更新待估计的参数,而变分贝叶斯则是叠代并更新待估计的参数和函数(这里的函数具体指的是:后验概率P(Z|X),估计的结果为Q(Z),与其说估计,倒不如说是近似与替代)
(1)变分贝叶斯的两步叠代为:
E步骤: 最大化L(Q) w.r.t. Q,此时θ固定,受Q约束,等效最小化;(详细请看EM算法)(因此,推理步骤试图找到最接近精确后验分布的q)
M步骤: 最大化L(Q) w.r.t. θ,此时Q固定;
参考:参考与链接1
(2)而EM算法的两步叠代为:

参考:参考与链接2
四、缺点及评价
为了使得目标函数可解,上述传统的变分推理方法通常假设变分分布是完全可分解的平均场形式(mean-field form),即强独立性的假设,这种假设忽略了变量间的相关性。但在实际应用中,变量间相关性不可忽略,否则导致降低变分推理方法近似的准确性。
为了建模变量间的相关性,可使用以下方法替代传统的平均场中的独立性的强假设:
(1)高斯推理方法(Gaussian approximation)
(2)变分推理方法
结构化的变分推理方法(structured variational inference)
层次化变分推理方法(hierarchical variational inference)
(3)copula 变分推理(copula variational inference,CVI)
而关于相关性的研究可参考《变分推理及贝叶斯方法在主题模型中应用的研究》等文献。