keras 卷积原理分析
假设我们有这样一个2D卷积模型
modle = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu', input_shape=(150, 150, 3)))
model.add(Maxpooling2D((2, 2)))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D((2, 2))
model.add(Conv2D(128, (3, 3), activation='relu'))
model.add(MaxPooling2D((2, 2))
model.add(Flatten())
model.add(Dense(512, activation='relu'))
model.add(Dense(1, acativation='sigmoid'))
首先我们输入的为(img_col, img_row, channels) = (150, 150, 1)的图像。
根据卷积原理,第一层卷积之后得到(148, 148, 32)。这里我们知道卷积层的第一个输入值为filter, 即过滤器的数量,也是输出维度。第二个参数即为filter_size。Padding:表示是否填充,如果设置padding=same,那么输出就为(150, 150, 32)。
如果我们输入如下一张图像。
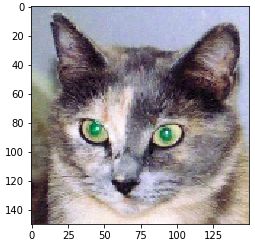
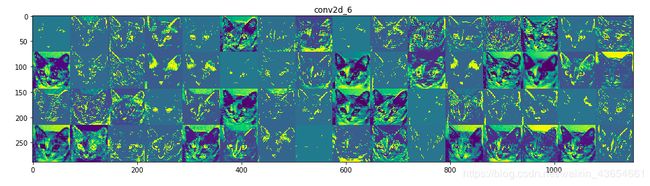
那么第一层卷积之后就得到如下输出,共有32张特征图:

Maxpooling之后得到(76, 76, 32),(通俗来讲就是抽样吧)。
然后进行第二次卷积,这个时候filter=64,kernel_size=(3, 3)。得到输出结果为(72, 72, 64)
注意:本来我们池化之后得到(74,74, 32),第二此卷积filter=64, 如果我们对第一层得到的每一张feature_map都做卷积的话,我们应该得到(74, 74, 64, 32)才对啊!其实只要这样理解就行了:第二层的每一个filter确实是对每一张feature_map做了卷积,但是讲32个卷积结果相加就得到第二层的feature_map值,所以第二层卷积之后得到的
(72, 72, 64)
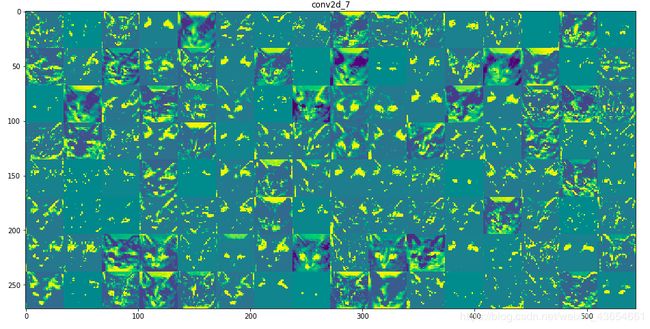
然后第二层卷积之后得到如下结果:
第三层卷积之后:
这样,通过卷积我们就能得到一张图像的很多特征细节,虽然对于我们人类来说很难识别,但是对于机器来说用来做识别却是再好不过。若果我们继续下分下去,我们就能得到下图所示一样的基本特征。然后我们讲这些得到特征图Flatten()之后放入到全连接网络,用来做识别或者其他什么的。
最后我们再看看我们学习得到的filter是长啥样的。


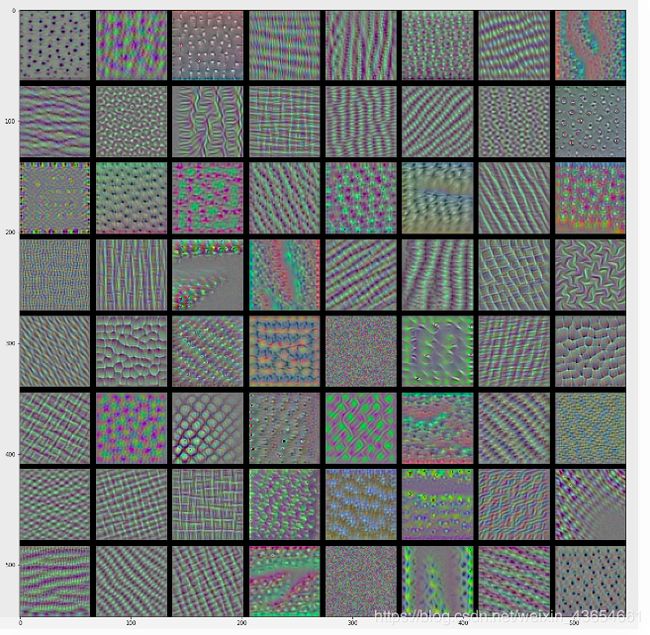

感觉很神奇吧!!!
这些filter不就是deep dream 中出现的涂鸦吗!!
参考:
https://github.com/fchollet/deep-learning-with-python-notebooks